Repeating Decimals

There are decimals in which some digits in the fractional part are infinitely repeated. These decimals look like this:

0.66666666666666…

0.33333333333333…

0.68181818181818…

Decimals of this type are called Recurring (repeating) Decimals. In this lesson we will try to figure out what these fractions are and how to work with them.

We get a repeating decimal

Let's try to divide 1 by 3. We won't talk much about how it works: we learned how long division works in detail in the lesson Operations with decimals.

So, divide 1 by 3

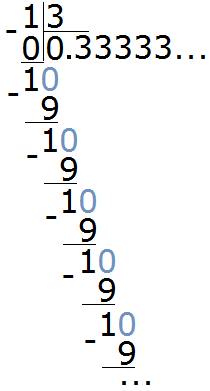
You can see that we constantly get a remainder of 1, then we add 0 to it and divide 10 by 3. And this is repeated over and over again. As a result, the fractional part is 3 each time. Dividing 1 by 3 will be done indefinitely, so it makes more sense to stop there.

These fractions are called periodic fractions because they have denominators that repeat infinitely (repeating cycle of digits). The "cycle" (period) may consist of several digits, or it may consist of one digit, as in our example.

In the example above, the period in the decimal 0.33333 is the number 3. Usually such decimals are written in a short form.

First you write the whole part, then you put a decimal point and in parentheses you write the period (cycle) (the digit/digits that repeats).

In our example, the number 3 is repeated; it is the period in the decimal 0.33333. Therefore, a short form will look like this:

0. (3)

It reads "zero and three in a period".

Example 2. Divide 5 by 11

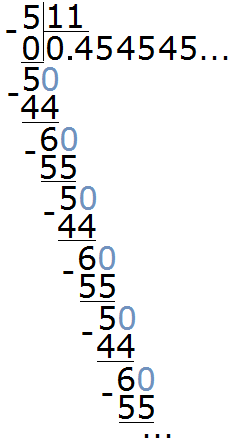
This is also a periodic fraction. The period of this fraction is the digits 4 and 5, these digits are repeated infinitely. A short form of this recurring decimal will look like this:

0. (45)

It reads like  "zero point forty-five in a period".

Example 3. Divide 15 by 13

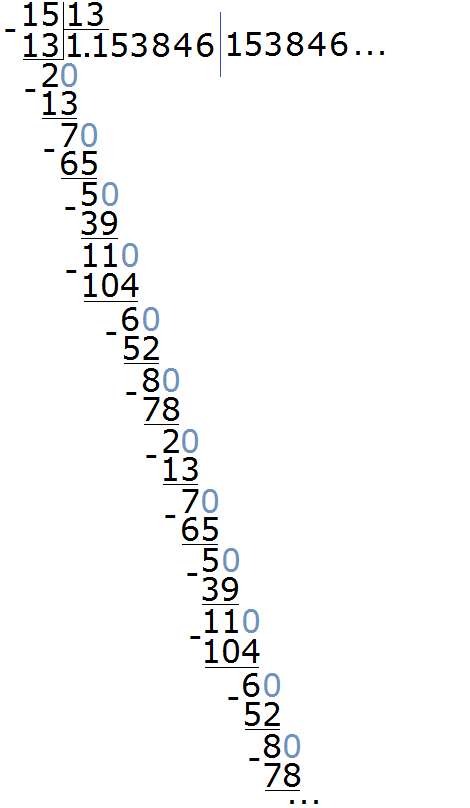
Here the period consists of several digits, namely the digits 153846. For clarity, the period is separated by a blue line. The short form for this recurring decimal would look like this:

1. (153846)

It reads as: "one hundred and fifty-three thousand eight hundred and forty-six in a period".

Example 4. Divide 471 by 900

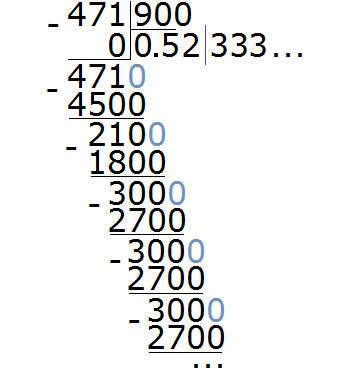
In this example, the period does not start immediately, but after the numbers 5 and 2. The short form for this recurring decimal will look like this:

0. 52 (3)

It reads as: "zero point fifty-two and three in a period."

Types of repeating decimals

There are two types of periodic decimals: Purely periodic decimal and periodic decimal .

If a repeating decimal has a period beginning immediately after the decimal point, it is called Purely periodic. For example, the following repeating decimal are pure:

0. (3)

0. (6)

0. (5)

You can see that in these decimals the period begins immediately after the decimal point.

If the period in a repeating decimal begins not immediately, but after some number of non-repeating digits, then such a decimal is called a repeating decimal . For example, the following decimals are repeating decimals:

0.52 (3)

0.16 (5)

0.31 (6)

You can see that in these decimals the period does not start immediately, but after a certain number of non-repeating digits.

How to round repeating decimals

Just as a lizard gets rid of its tail, we can get rid of a repeating decimal from a recurring period. To do this, it is sufficient to round that repeating decimal to the desired period.

For example, round the repeating decimal 0. (3) to the hundredth place. To see the retained and discarded digit, temporarily write the fraction 0. (3) not in abbreviated form, but in full:

Do you remember the rounding rule? If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down.

So the repeating decimal 0. (3) when rounded to a hundredth turns into a decimal 0.33

0. (3) ≈ 0.33

Let us round the repeating decimal 6.31 (6) to the thousandth place.

Write down the fraction in its full form to see the retained and discarded digit:

Remember the rounding rule. If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up.

So the repeating decimal on 6.31 (6) when rounded to the thousandths turns into a fraction 6.317

6.31 (6) ≈ 6.317

Converting repeating decimals to fractions

Converting a purely repeating decimal to fractions is an operation that we will use rather rarely. Nevertheless, for general knowledge , it is important to study this as well. We will begin by converting a pure repeating decimal into an ordinary fraction.

We have already said that if a period in a repeating decimal begins immediately after the decimal point, such a fraction is called a purely periodic.

To convert a purely repeating decimal into an ordinary fraction, write the period of the repeating decimal in the numerator of the ordinary fraction, and write some number of nines in the denominator of the ordinary fraction. In this case, the number of nines must be equal to the number of digits in the period of the repeating decimal .

As an example, consider a purely repeating decimal 0. (3) - zero integers and three in the period. Let's try to convert it into a fraction.

The rule states that the period of a repeating decimal should be written first in the numerator of an ordinary fraction.

So in the numerator we write the period of the decimal 0. (3) that is three:

And the denominator must contain some number of nines. In this case, the number of nines must be equal to the number of digits in the period of the repeating decimal 0. (3).

In the repeating decimal 0. (3) the period consists of one digit 3. So we write one nine in the denominator of the fraction:

The resulting fraction can be reduced by 3, then we get the following:

We got an ordinary fraction of .

Thus, when you translate the repeating decimal 0. (3) into an ordinary fraction, you get

Example 2. Convert the repeating decimal 0. (45) into an ordinary fraction.

Here the period is two digits 4 and 5. Write these two digits in the numerator of the fraction:

And in the denominator we write some number of nines. The number of nines must be equal to the number of digits in the period of the repeating decimal 0. (45).

In the repeating decimal 0. (45) the period consists of two digits 4 and 5. So we write two nines in the denominator of the fraction:

The resulting fraction can be reduced this fraction by 9, then we get the following:

Thus, when you convert the repeating decimal 0. (45) into an ordinary fraction, you get

Converting mixed repeating decimals to fractions

To convert a mixed repeating decimals to fractions, write in the numerator the difference where the minuend is the digits standing after the point in the fraction and the subtrahend are the digits standing between the point and the first period of the fractions.

For example, convert the mixed repeating decimal 0.31 (6) to fraction.

First, write the difference in the numerator. All digits after the decimal point (including the period) will be the decomposer, and the digits between the decimal point and the period will be the subtraction:

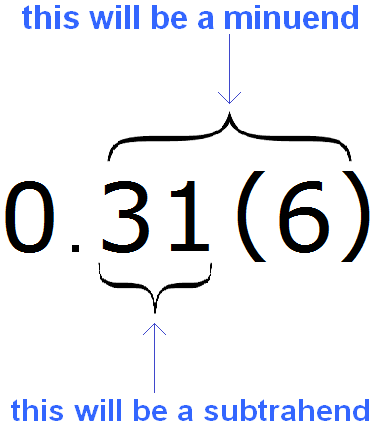
So we write the difference in the numerator:

And in the denominator we write some number of nines and zeros. The number of nines must be equal to the number of digits in the period of the periodic fraction 0.31 (6)

In the decimal 0.31 (6), the period consists of one digit. So we write one nine in the denominator of the fraction:

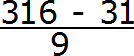
Now add the number of zeros. The number of zeros must be equal to the number of digits between the decimal point and the period of the periodic fraction.

In the fraction 0.31 (6) there are two digits between the decimal point and the period. So there must be two zeros in the denominator of the fraction. Add them:

We got an expression that is easy to calculate:

We got the answer

Thus, when you convert the periodic fraction 0.31 (6) to fraction, you get

Example 2. Convert the mixed repeating decimal 0.72 (62) into a to fraction

First, write the difference in the numerator. All digits after the decimal point (including the period) minus  the digits between the decimal point and the period:

So we write the difference in the numerator:

And in the denominator we write some number of nines and zeros. The number of nines must be equal to the number of digits in the period of the repeating decimal 0.72 (62)

In 0.72 (62) decimal the period consists of two digits. So we write two nines in the denominator of the fraction:

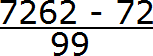
Now add the number of zeros. The number of zeros must be equal to the number of digits between the decimal point and the period of the repeating decimal .

In the fraction 0.72 (62) there are two digits between the decimal point and the period. So there must be two zeros in the denominator of the fraction. Add them:

We got an expression that is easy to calculate:

The answer is 

So when you convert the periodic fraction 0.72 (62) into an ordinary fraction, you get

Video lesson

Add comment