Direct and inverse proportions

Proportionality - equality between two ratios, is the relationship between two quantities in which a change in one quantity causes the other quantity to change by the same factor.

Proportion can be direct or inverse. In this lesson we will look at each of them.

Direct Proportion

Let us assume that the car is moving at a speed of 50 km/h. We remember that speed is the distance traveled in a unit of time (1 hour, 1 minute, or 1 second). In our example the car moves at 50 km/h, which means that in one hour it will cover a distance of 50 kilometers.

Let's show in the diagram the distance traveled by the car in one hour

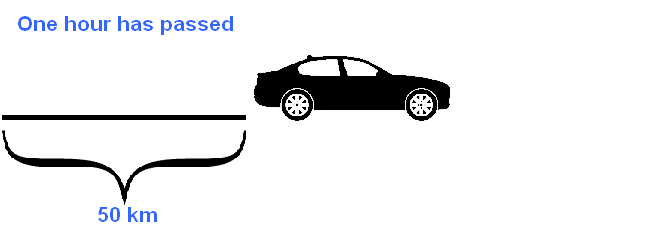
Let the car drive one more hour with the same speed equal to fifty kilometers per hour. Then it turns out that the car will travel 100 km

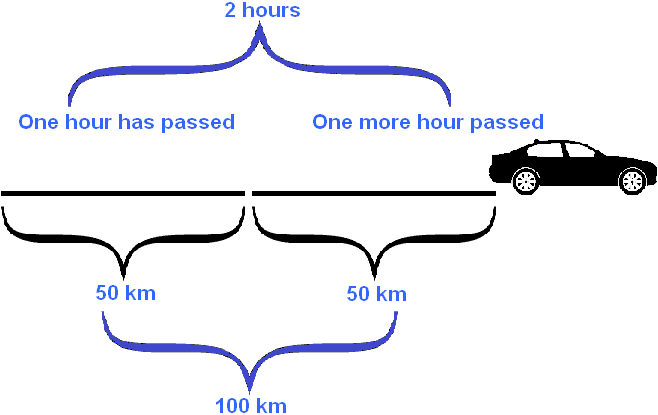
As you can see from the example, doubling the time resulted in an increase in the distance traveled by the same factor, i.e., twofold.

Such quantities as time and distance are called directly proportional. And the relationship between these quantities is called direct proportion .

Direct proportion is the relationship between two quantities in which an increase in one entails an increase in the other by the same factor.

And vice versa, if one quantity decreases by a certain number of times, then the other quantity decreases by the same number of times.

Suppose that it was originally planned to drive a car 100 km in 2 hours, but after driving 50 km, the driver decided to rest. Then it turns out that reducing the distance by half, the time is reduced by the same factor. In other words, decreasing the distance traveled will result in decreasing the time by the same factor.

An interesting feature of directly proportional quantities is that their ratio is always constant. That is, if the values of the directly proportional quantities change, their ratio remains unchanged.

In the example above, the distance was 50 km, and the time was one hour. The ratio of distance to time is 50.

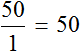
But we doubled the travel time, making it equal to two hours. As a result, the distance traveled increased by the same factor, i.e., it became equal to 100 km. The ratio of one hundred kilometers to two hours is again the number 50

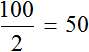
The number 50 is called the coefficient of direct proportionality (or proportionality constant). In this case, the coefficient is the speed of movement, because speed is the ratio of the distance traveled to time.

Proportions can be made from directly proportional quantities. For example, the ratios and make a proportion:

This attitude can be read as follows:

Fifty kilometers refers to one hour as one hundred kilometers refers to two hours.

Example 2. The cost and quantity of the purchased goods are directly proportional values. If 1 kg of candy costs $30, then 2 kg of the same candy will cost $60, and 3 kg will cost $90. As the cost of the purchased product increases, its quantity increases by the same factor.

Since the cost of goods and their quantity are directly proportional quantities, their ratio is always constant.

Let us write down the ratio of thirty rubles to one kilogram

Now write down what the ratio of sixty dollars to two kilograms equals. This ratio will again be equal to thirty:

Here the coefficient of direct proportionality is the number 30. This coefficient shows how many dollars we pay per kilogram of candy. In this example, the coefficient is the price of one kilogram of goods, because price is the ratio of the cost of goods to their quantity.

Inverse proportion

Consider the following example. The distance between the two cities is 80 km. The motorcyclist left the first city and drove at a speed of 20 km/h to the second city in 4 hours.

If the speed of the motorcyclist was 20 km/h, it means that every hour he traveled a distance equal to twenty kilometers. Let's graph the distance traveled by the motorcyclist and the time he traveled:

On the way back the speed of the motorcyclist was 40 km/h, and for the same route it took him 2 hours.

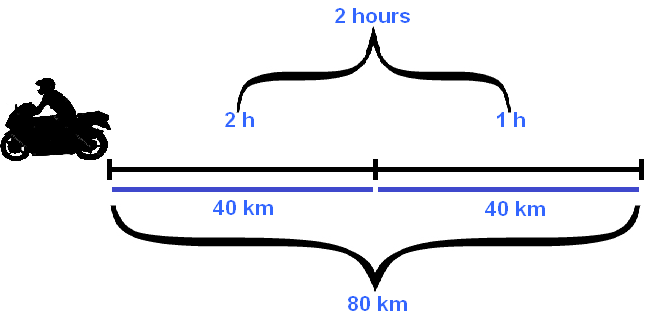
It is easy to see that when you change the speed, the time of movement has changed by the same factor. And it has changed in the opposite direction - that is, the speed has increased, and the time on the contrary has decreased.

Such quantities as speed and time are called inversely proportional. And the relationship between such quantities is called inverse proportionality.

Inverse proportion is the relationship between two quantities in which an increase in one quantity causes the other quantity to decrease by the same factor.

Conversely, if one quantity decreases by a certain number of times, then the other increases by the same number of times.

For example, if on the way back the speed of the motorcyclist was 10 km/h, then the same 80 km he would overcome in 8 hours:

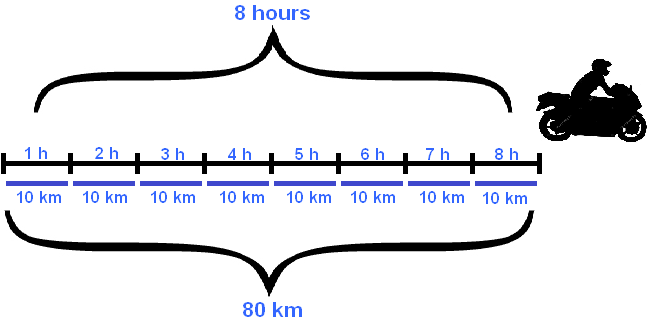
As can be seen from the example, a decrease in speed led to an increase in the time of motion by the same factor.

The peculiarity of inversely proportional quantities is that their product is always constant. That is, if the values of the inversely proportional quantities change, their product remains unchanged.

In the example considered, the distance between the cities was 80 km. When you change the speed and time of the motorcyclist, this distance always remained the same

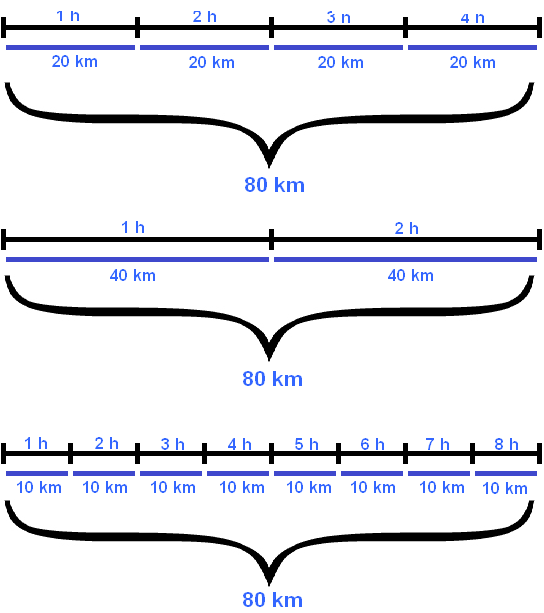
A motorcyclist could travel this distance at a speed of 20 km/h in 4 hours, and at a speed of 40 km/h in 2 hours, and at a speed of 10 km/h in 8 hours. In all cases, the product of speed and time is 80 km

80 km = 20 km/h * 4 h

80 km = 40 km/h * 2 h

80 km = 10 km/h * 8 h

Video lesson

Add comment