In this lesson, we will learn about something that we did not mention when we studied fractions because we thought they were difficult to learn at first.
Proper and improper fractions
Early on in our study of fractions, we learned that a proper fraction is one in which the numerator is smaller than the denominator.
In school books we can find another definition of a proper fraction. It looks like this:
"A proper fraction is always less than 1."
How do we understand this definition? A fraction by itself indicates that some object is divided into several parts. And it is always one single object. This is what is meant by a unit.
For example, let's say we have one pizza:

In this case, it is the unit.
If we cut off half of this pizza, that is, ![]() (one-second of the pizza), then our slice will be smaller than the whole pizza:
(one-second of the pizza), then our slice will be smaller than the whole pizza:

This is the essence of the phrase "a proper fraction is always less than one".
Our pizza half is a fraction of ![]() and it is less than one whole pizza, which is less than one:
and it is less than one whole pizza, which is less than one:
![]()
This expression can be proved. If we calculate the fraction ![]() , we get the decimal 0.5. And this is a rational number less than one:
, we get the decimal 0.5. And this is a rational number less than one:
![]()
On the number line you can see how these numbers are arranged:

You can see that the rational number 0.5 is to the left of 1. And we remember that the more to the left of the number on the number line, the smaller it is.
With improper fractions, it was the opposite. We called an improper fraction a fraction where the numerator is larger than the denominator.
But in school books you can find another definition of an improper fraction. It looks like this:
"An improper fraction is always greater than or equal to one."
For example, consider the improper fraction ![]() . Separate the whole part of the fraction, so we get
. Separate the whole part of the fraction, so we get ![]() . Let's represent this mixed number as one whole pizza and another half pizza:
. Let's represent this mixed number as one whole pizza and another half pizza:
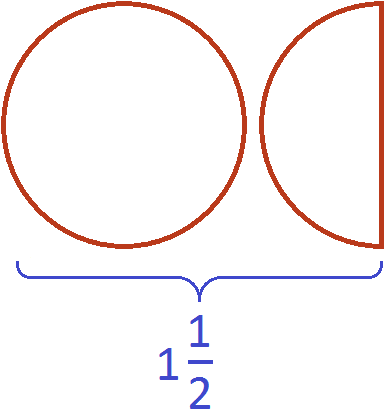
Together one whole pizza and another half pizza is more than just one whole pizza
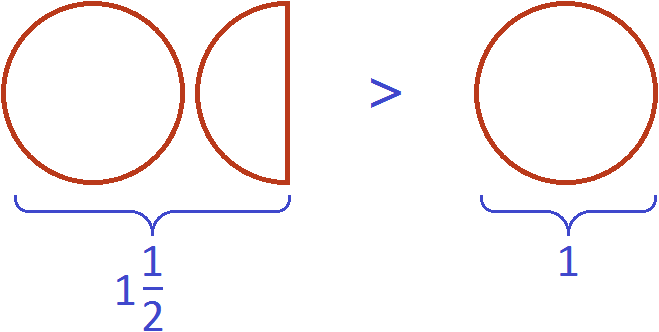
This is the essence of the phrase "an improper fraction is always greater than one".
One whole pizza and another half pizza is described by a mixed number of ![]() and that mixed number is greater than one:
and that mixed number is greater than one:
![]()
Let's convert the mixed number ![]() back to an improper fraction so as not to contradict the rule. After all, in this case we are talking about improper fractions:
back to an improper fraction so as not to contradict the rule. After all, in this case we are talking about improper fractions:
![]()
which schematically would look like this:
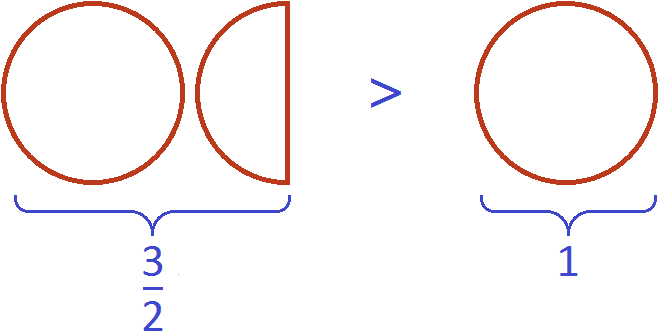
The expression ![]() can be proved. If we calculate the fraction
can be proved. If we calculate the fraction ![]() , we get the decimal 1.5. And this is a rational number greater than one:
, we get the decimal 1.5. And this is a rational number greater than one:
![]()
On the number line you can see how these numbers are arranged:

You can see that the rational number 1.5 is more to the right than 1. And we remember that the more right the number is on the number line, the larger it is.
A fraction equal to one is also called an improper fraction. We are talking about those fractions in which the numerator and denominator are equal.
Consider the fraction ![]() . Picture it as two identical slices of pizza:
. Picture it as two identical slices of pizza:
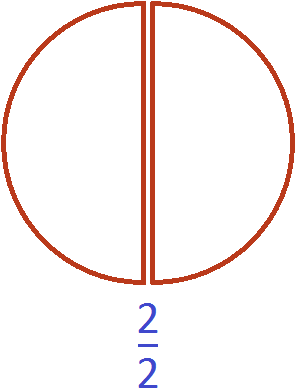
In fact, we are not talking about fractions, but one whole pizza:
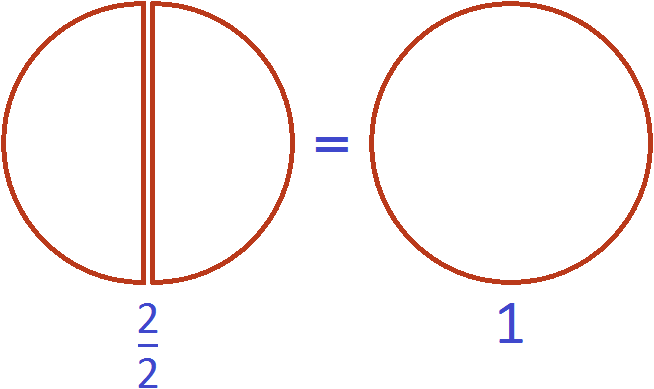
This is the essence of the phrase "an improper fraction can equal one".
![]()
Any integer other than zero (not equal to zero) can be represented as an improper fraction with a denominator of 1. For example, the numbers 3, 5, 9, 12 can be represented as improper fractions with denominator 1
![]()
Representing an object as a unit makes it easier to solve problems. Let's look at some examples.
Example 1. One chocolate bar is bought. A third of it was cut off. How many bars are left?
Two-thirds of the candy bar is left. The candy bar itself can be described by the number 1, then subtract a third from that unit:
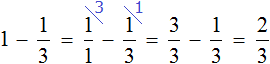

Without giving any calculations on paper, it is possible to answer the question of such a problem. If you say "cut off a third", then you should immediately note that the denominator is 3.
If you cut off one part out of three, how many parts should be left? That's right, two parts. So the answer is "two parts of three" or "two-thirds".
Example 2. One pie is bought. Two sixths of it were cut off. How many pies are left?
There are four sixths of a pie left. The pie itself can be described by the number 1, then subtract two sixths from this unit:
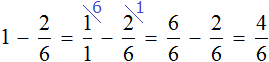
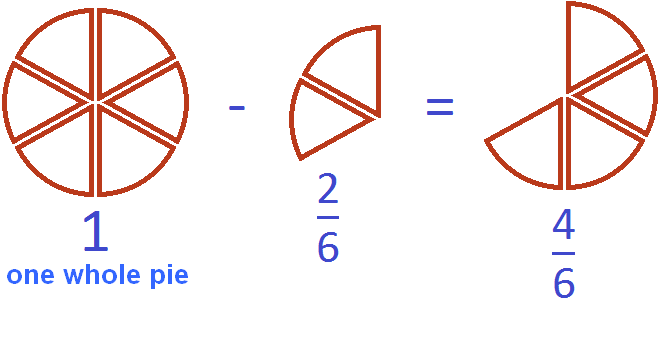
Reducing fractions to a common denominator
To reduce the fractions to a common denominator, we have to find the LCM (least common multiple) of the denominators of these fractions. Then we need to divide the found LCM by the denominator of the first fraction and obtain an additional multiplier for the first fraction.
We do the same for the second fraction - we divide the LCM by the denominator of the second fraction and get an additional multiplier for the second fraction.
Then the fractions are multiplied by their additional multipliers. As a result, they are converted into fractions with the same denominators.
For example, the expression ![]() is calculated as follows:
is calculated as follows:
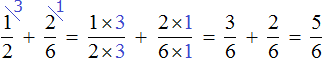
But there is another way to reduce fractions to a common denominator. This method is often used by schoolchildren and lazy students. The essence of this method is that the denominators of both fractions become additional multipliers, and it happens "crosswise" - the denominator of the first fraction becomes an additional multiplier of the second fraction, and the denominator of the second fraction becomes an additional multiplier of the first fraction.
Calculate the previous expression ![]() this way. The denominator of the first fraction 2 becomes an additional factor of the second fraction, and the denominator of the second fraction 6 becomes an additional factor of the first fraction:
this way. The denominator of the first fraction 2 becomes an additional factor of the second fraction, and the denominator of the second fraction 6 becomes an additional factor of the first fraction:
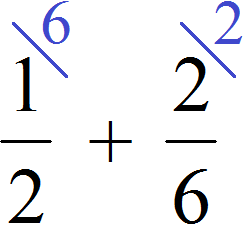
Then multiply the numerator and denominator of each fraction by its additional multiplier and calculate:
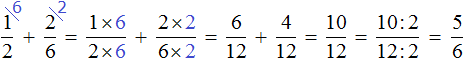
The advantage of this method is that it is not necessary to find the LCM of the denominators of both fractions. In the process of calculation, everything aligns itself. The only disadvantage is that the expression becomes longer and sloppier.
Compare the expressions that we calculated first by the first method and then by the second method:
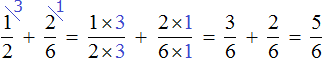
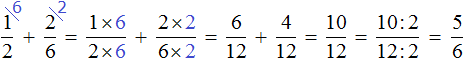
An expression calculated by the first method is much neater and shorter than the second.
We will use the second method when studying algebra. In algebra we have to work with letter expressions more often than with number expressions.
For example, if we are to reduce the alphabetic expression ![]() to a common denominator, we will have no choice but to use the "crosswise" method, that is, the second method, which we have just considered:
to a common denominator, we will have no choice but to use the "crosswise" method, that is, the second method, which we have just considered:
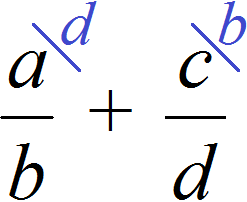
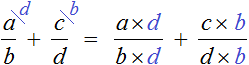
Finding fractions from a number
To find a fraction of a number, we divide the number by the denominator of the fraction and multiply the result by the numerator of the fraction.
For example, to find ![]() of 10 centimeters, you need to divide 10 by 5, and multiply the result by 2.
of 10 centimeters, you need to divide 10 by 5, and multiply the result by 2.
10 : 5 = 2
2 × 2 = 4
The answer is 4. So ![]() of ten centimeters is 4 centimeters. Schematically it looks like this:
of ten centimeters is 4 centimeters. Schematically it looks like this:
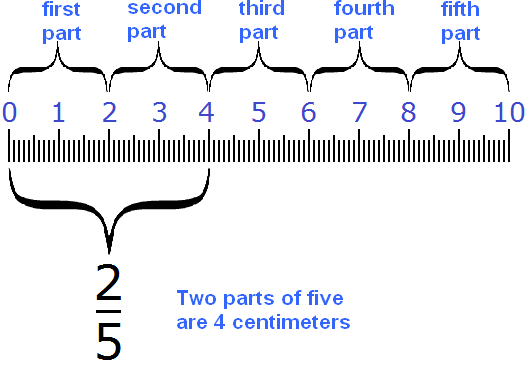
To find ![]() of ten centimeters, just multiply 10 by
of ten centimeters, just multiply 10 by ![]() . Then we get the same result as last time, but we get it in one step:
. Then we get the same result as last time, but we get it in one step:
![]()
Therefore, we can take note of the following rule for finding a fraction of a number:
To find a fraction of a number, multiply the number by the fraction you are looking for.
Example 2. Find ![]() of two hours.
of two hours.
Two hours is 120 minutes. To find ![]() of 120 minutes, multiply 120 by a fraction of
of 120 minutes, multiply 120 by a fraction of ![]()
![]()
So ![]() of two hours is 80 minutes.
of two hours is 80 minutes.
Finding a number with a fraction
To find the whole number by its fraction, we divide the number by the numerator of the fraction and multiply the result by the denominator of the fraction.
For example, knowing that ![]() of the tape measure is 12 cm, we can find the length of the entire tape measure. To do this, divide 12 by 2, and multiply the result by 3.
of the tape measure is 12 cm, we can find the length of the entire tape measure. To do this, divide 12 by 2, and multiply the result by 3.
12 : 2 = 6
6 × 3 = 18
We got 18. So the length of the whole tape measure is 18 cm.
But there is a second version of the solution. To find the length of the whole tape measure, just divide 12 by a fraction of ![]() . Then we get the same result as last time, but we get it in one step:
. Then we get the same result as last time, but we get it in one step:
![]()
Therefore, you may want to take note of the following rule for finding a number by a fraction:
To find a number by a fraction, divide the number by the fraction.
Example 2. ![]() of the whole path is 6 km. Find the length of the entire path.
of the whole path is 6 km. Find the length of the entire path.
To find the length of the entire path, simply divide 6 by the fraction ![]() .
.
![]()
The answer is 15. So the length of the entire path is 15 kilometers.
Decimal point in decimals
In other countries (non-English-speaking) they put a comma instead of a dot in the decimal, and this should not bother you - it's the same thing.
The decimal point is used to increase or decrease a fraction by a factor of 10, 100, 1000 or more. When you multiply a decimal by 10,100,1000...., the decimal point moves to the right, and when you divide it by 10,100,1000..., it moves to the left.
Example 1. Multiply the decimal 6.3 by 10.
If you want to multiply the decimal 6.3 by 10, just move the decimal point to the right by one digit to get 63.
Example 2. Divide a decimal 6.3 by 10.
If you want to divide a decimal 6.3 by 10, just move the decimal point to the left by one digit, we get 0.63
To answer the question "How do I know how many digits to move the decimal point?", you need to look at how many times the decimal increases (or decreases).
- If the decimal is to be multiplied (or divided) by a ten, the decimal point is moved by one digit.
- If the decimal is to be multiplied (or divided) by one hundred, the decimal point is shifted by two digits.
- If the decimal is to be multiplied (or divided) by one thousand, the decimal point is shifted by three digits.
In general, it all depends on the number of zeros in the multiplier.
For example, If you want to multiply a decimal by a factor of ten, that means to multiply it by 10. We remember that in order to multiply a decimal by 10, we need to move the decimal point to the right by one digit in the decimal (since there is one zero in number 10). Now there is no need to memorize such rules. This multiplication can easily be done by moving the decimal point.
Example 3. Multiply the decimal 6.3 by one thousand.
To increase the decimal 6.3 a thousand times, just move the decimal point to the right by three digits, we obtain 6300. If there are not enough digits after the decimal point, then instead of the missing digits write zeros, which is what we did.
Example 4. Divide the decimal 12.5 by one hundred .
To reduce a decimal 12.5 by a hundred times, just move the decimal point to the left by two digits, we obtain 0.125
The decimal point can be used not only in decimals. It can be used with common integers too.
For example, take an integer 325 and put a dot at the end of it, we get 325 with a dot. We will use the dot this time, as it is easier to represent in the figure:

Let's try to reduce this number by a factor of ten. To do this, just move the point to the left by one digit, we get 32.5

Let's try to increase the number 123 a thousand times. To do this, just move the decimal point three digits to the right, we get 123000.
Let's try to reduce the number 123 by a thousand times. To do this, just move the decimal point three digits to the left, we get 0.123
Let's try to reduce the number 65 by a thousand times. To do this, just move the decimal point three digits to the left, we get 0.065
Let's try to increase the number 65 by a hundred times. To do this, just move the decimal point two digits to the right, we get 6500.
Adding, subtracting, multiplying, and dividing several fractions
There are problems in which you need to calculate an expression composed of several fractions. For example,
![]()
Such an expression is calculated according to the order of operations. In this case the calculation will be performed sequentially from left to right:
![]()
If you subtract ![]() pizza from
pizza from ![]() pizza, then add
pizza, then add ![]() pizza, then subtract
pizza, then subtract ![]() pizza, that leaves
pizza, that leaves ![]() pizza
pizza

If you have trouble understanding this example, try to solve it on paper, making appropriate drawings for each fraction.
Example 2. Find the value of the expression ![]()
In this example, multiply first, then add and subtract
![]()
![]()
If ![]() pizza is doubled, you get one whole pizza
pizza is doubled, you get one whole pizza
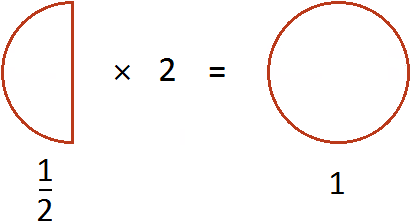
Then if you add this whole pizza to ![]() pizza and then subtract
pizza and then subtract ![]() pizzas from the result, you get
pizzas from the result, you get ![]() pizza
pizza
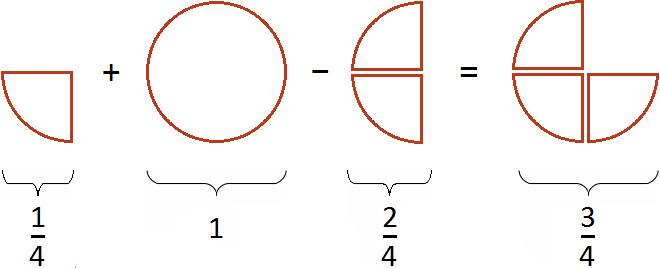
Example 3. Find the value of the expression ![]()
First, it is desirable to calculate the expressions in the numerators of both fractions, namely the expressions 2-1 and 1+1,
![]()
Further calculation is not very difficult ![]() +
+ ![]() =
= ![]()
![]()
Of course, you could write the expressions in the numerators of both fractions in the same numerator. This would not change the answer:
![]()
But in some cases, there may be some catch, especially if one fraction is subtracted from another fraction. The following example demonstrates this.
Example 4. Find the value of the expression ![]()
Calculate the expressions in the numerators of both fractions, namely the expressions 2+1 and 2-1
![]()
And it is not hard to guess that ![]() equals
equals ![]() or
or ![]() (assuming that the fraction
(assuming that the fraction ![]() is reduced by 2)
is reduced by 2)
![]()
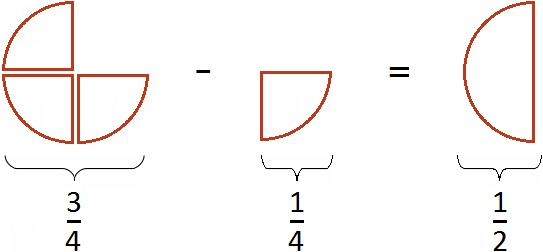
It all makes sense. If you subtract ![]() pizza from
pizza from ![]() pizza, you get
pizza, you get ![]() pizza.
pizza.
Now let's try to solve this example by writing both expressions in the numerators of both fractions in the same numerator:
![]()
That's not the right answer at all. This answer is not correct. Let's see what the expression ![]() is.
is.
To begin with, write it down as follows:
![]()
Now let's try to trace the whole process of calculating this expression. Suppose there were ![]() pizzas
pizzas

Another ![]() pizza was added to it.
pizza was added to it.
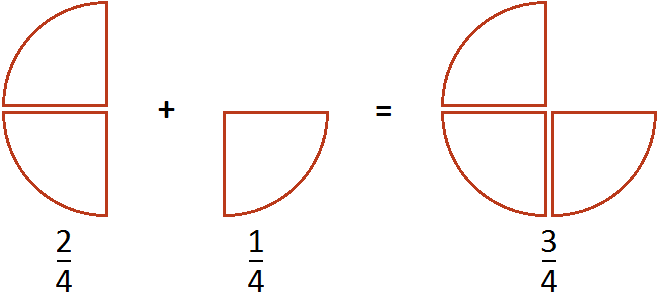
Then ![]() of the pizza is subtracted from the resulting
of the pizza is subtracted from the resulting ![]()
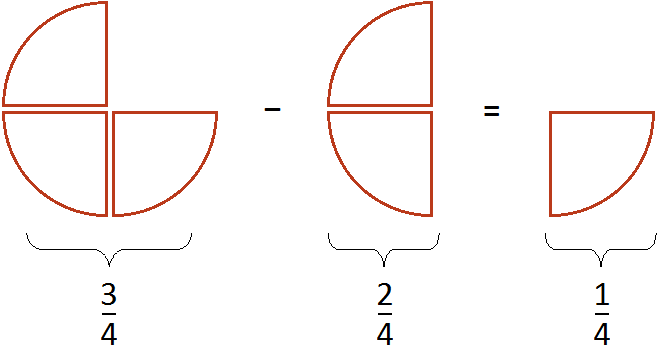
Then subtract another ![]() pizza from the resulting
pizza from the resulting ![]() pizza
pizza
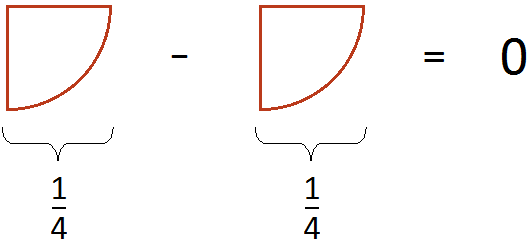
The result is 0, which means that the pizza is gone. But we know there should have been ![]() of a pizza left. So you should be careful when calculating fractional expressions, especially when subtracting expressions that have other expressions in the numerator.
of a pizza left. So you should be careful when calculating fractional expressions, especially when subtracting expressions that have other expressions in the numerator.
If you want to save time and write both expressions in the numerator of both fractions, the second numerator should be in parentheses. This will save you from making a mistake:
![]()
Example 5. Find the value of the expression ![]()
Calculate the expressions in the numerators of both fractions:
![]()
Let's reduce these fractions to a common denominator and calculate the resulting expression as usual:
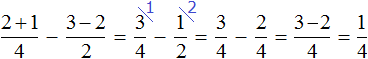
If you subtract ![]() pizza from
pizza from ![]() , you get
, you get ![]() pizza
pizza

Example 6. Find the value of the expression ![]()
The first thing to do is to perform multiplication:
![]()
Next, the addition is performed:
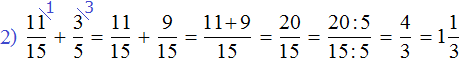
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.