In this lesson we will study multiplication. Let me recall that the multiplication table is designed to multiply small numbers. Be sure to learn it by heart, because any multiplication of large numbers eventually consist of multiplication of small numbers.
Single and multi-digit numbers
First, let's introduce two new concepts: single-digit and multi-digit numbers.
Definition. A single-digit number is a number that consists of one digit. For example, the following numbers are single digits:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The word "single digits" speaks for itself. One-digit means it consists of a single digit (a digit is sometimes called a sign).
Definition. A multi-digit number is a number that consists of two or more digits. For example, the following digits are multi-digit numbers:
10, 11, 15, 255, 350, 1000, 12500
There are an infinite number of multi-digit numbers. They cannot be counted. In addition, they are divided into the following types:
- two-digit numbers that consist of two digits (e.g., 25);
- three-digit numbers that consist of three digits (for example, 563);
- four-digit numbers that consist of four digits (e.g., 1400)
and so on, depending on how many digits are in the number.
Multiplication of single-digit numbers
One-digit numbers are easy to multiply. All you need to know is the multiplication table. Examples:
5 x 5 = 25
3 x 5 = 15
7 x 6 = 42
5 x 8 = 40
If for some reason you can't remember the multiplication table, you can use addition. After all, multiplication is nothing more than multiple addition operations.
To multiply, for example, the number 4 by the number 3, you need to add 4 three times:

Multiplication by 10, 100, 1000
To multiply any number by 10, 100 or 1000, just add to the first multiplier the number of zeros from the 10/100/1000.
For example, to multiply 12 by 10, you need to add zero from the multiplier 10 to the multiplier 12. The answer is 120

More examples:
12 x 100 = 1200 (two zeros were added to 12 because there are two zeros in the number 100)
12 x 1000 = 12000 (add three zeros to 12, because there are three zeros in the number 1000)
15 x 100 = 1500 (two zeros were added to 15, because there are two zeros in number 100)
320 x 100 = 32000 (two zeros were added to 320, because there are two zeros in 100)
If it is not the multiplier that ends with zero, but the other one, then you should add zero after the second multiplier in order to get the answer.
For example, to multiply 10 by 12, you should write in the answer the multiplier 12 and add one zero at the end:
10 x 12 = 120
Multiplication of numbers that end with zeros
If both numbers end with zeros, then multiply those digits that are not zeros, then add all zeros from both numbers to the result.
Example 1. multiply 20 by 30.
20 x 30
We see that both numbers contain zero. First we multiply the digits that are not zeros. These are the digits two and three. Two multiplied by three is six:
20 x 30 = 6
Now add all zeros from both numbers to the result, that is, to the number 6. Number 20 has one zero, number 30 also has one zero. Total two zeros. We add two zeros to number 6
20 x 30 = 600
Example 2. Multiply 40 by 300
First multiply the digits that are not zeros. These are the digits 4 and 3. Four times three is twelve:
40 x 300 = 12
Now add all zeros from both numbers to the result, that is, to the number 12. Number 40 has one zero, number 300 has two zeros. Total three zeros. We add three zeroes to number 12
40 x 300 = 12000
Example 3. Multiply 600 by 3000
First multiply the digits that are not zeros. These are the digits 6 and 3. Six multiplied by three is eighteen:
600 x 3000 = 18
Now add all zeros from both numbers to the result, that is, to the number 18. Number 600 has two zeros, number 3000 has three zeros. That makes five zeros. We add five zeroes to number 18
600 x 3000 = 1800000
Multiplication of a multi-digit number by a single-digit number
To multiply a multi-digit number by a single-digit number, multiply each digit of the multi-digit number by that single-digit number. For example, find the value of the expression 12 x 3. Write this expression in a column, with the ones under the ones. All this is connected by the multiplication sign ( x )
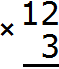
Next, each digit of a multi-digit number is multiplied by 3. We start multiplying from the digit one, that is, from the digit 2. Two multiplied by three is six. Write the digit 6 in the units division of our answer:
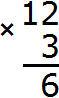
Now multiply 1 by 3 to get 3. Write the number 3 in the tens place of our answer:
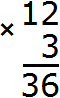
The answer is 36.
In this example, the multiplier was 12 and the multiplier was 3. The number 12 is two ones and one tens. Our problem was to increase these two ones and one tens by a factor of 3. Then, solving this example, we could reason as follows:
Increase two units by a factor of three: 2 x 3 = 6. We have six units. Write the number 6 in the units division of the new number
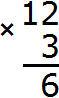
Let's increase one tens by three times: 1 x 3 = 3. We have three tens. Write the number 3 in the tens division of the new number:
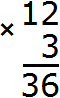
Sometimes multiplying one digit of a multi-digit number by a single-digit number results in a multi-digit number. In this case, first write down one digit from the units digit, and transfer the remaining digits to the next digit to which they will be added after the calculation.
For example, find the value of the expression 23 x 6
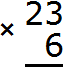
Multiply each digit of 23 by 6. We start with a 3: 3 x 6 = 18. Eighteen does not fit in the unit digit of our answer, so 8 is written first, and 1 is carried over to the next digit. This unit will be added to the result of multiplying 2 by 6.

Now multiply 2 by 6 to get 12, plus the one that came from the previous multiplication. In the figure this unit is highlighted in blue. Calculate (2 x 6) + 1 = 13
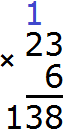
The answer is 138. In this example, the multiplier was 23 and the multiplier was 6. The number 23 is three ones and two tens.. Our problem was to increase these three units and two tens by a factor of 6. Then, solving this example, we could reason as follows:
Let's increase three units six times: 3 x 6 = 18. We got eighteen units. There is a digit overflow in the ones place value. Eighteen is eight ones and one tenth. Write 8 ones in the units category of the new number, and 1 tens in the tens category. We will add this tens when we increase two tens six times:

Let's increase two tens 6 times: 2 x 6 = 12. We have twelve tens. Add one tens left over from number 18.
Twelve tens plus one tenth is 13. Write 13 in the place of tens of the new number, forming the final answer:
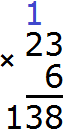
Example 3. Find the value of the expression 326 x 5
Write the expression in columns:
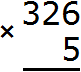
Multiply each digit of 326 by 5. We start with a six: 6 x 5 = 30. The number 30 does not fit in the units digit of our answer, so we write 0 first, and carry the three to the next digit:
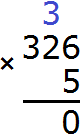
Now multiply 2 by 5, and we get 10 plus the three that came from the previous operation: (2 x 5) + 3 = 13. We obtain the number 13, which does not fit in the digit of tens of our answer. Therefore, we write down 3 first, and carry the one to the next digit:
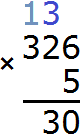
Now multiply the last three by 5, plus add the one that came from the previous operation: (3 x 5) + 1 = 16. We obtained 16. Write down this number in its entirety, forming the final answer:
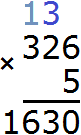
Multiplication of multi-digit numbers by multi-digit numbers
Multiplying multi-digit numbers by multi-digit numbers is done in the same way as multiplying multi-digit numbers by single-digit numbers. Each digit of a multi-digit number is multiplied by each digit of another multi-digit number. The only difference is that at the end there is a kind of staircase of answers that must be added up. Let's look at a few examples to get a good understanding of this.
Example 1. Find the value of the expression 12 x 14
Write down this expression in a column - ones under ones, tens under tens:
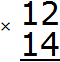
Now multiply each digit of 12 by each digit of 14. You should do this one by one, starting with four. As a result of these actions, we come to the multiplication of a multi-digit number by a single-digit number, which we studied earlier:
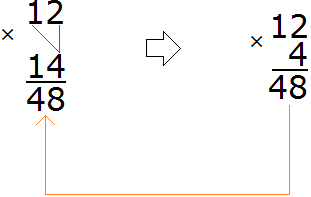
By multiplying 12 by 4, we got the number 48, which we wrote down so that the unit digit of this number is under the four by which we multiplied 12.
Now multiply 12 by 1:
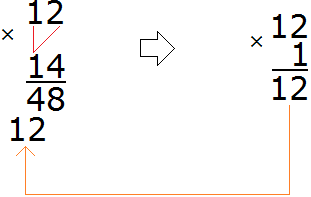
We multiplied 12 by 1 to get the number 12 and wrote it down so that the unit digit of this number is below the unit by which we multiplied 12.
We got the staircase of answers 48 and 12, which should be added. We add it up and get the answer 168.
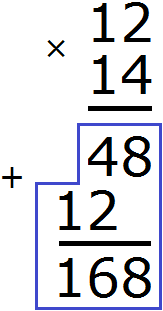
In this example, the factor 14 is four ones and one tenth. Then multiplying 12 by 14 can be understood as multiplying 12 by a factor of four and a factor of ten. This explains the appearance of the staircase at the end of the solution. Let's see how it looks at each step:
Let's multiply the number 12 by a factor of four and get the number 48.
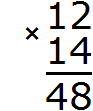
Increase the number 12 ten times, and you get the number 120. Write 120 so that the units of this number can be added to the units of 48, and the tens of 120 can be added to the tens of 48
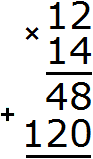
Now add up the resulting staircase of answers. We add ones to ones, tens to tens, and hundreds to hundreds. The result is the final answer:
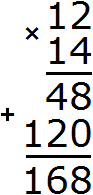
But most often the multiplier is not grouped with digits, and multiplication is done by multiplying each digit of the multiplier by each digit of the multiplier.
Example 2. Find the value of the expression 25 x 36
Write this expression in columns
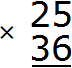
Multiply each digit of 25 by each digit of 36.
Multiply 25 by 6:
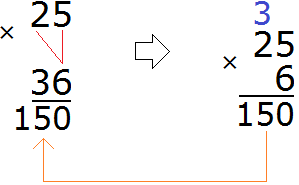
Multiply 25 by 3:

Now fold the resulting ladder:
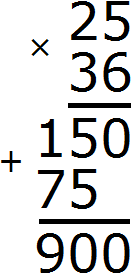
We got an answer of 900.
Consider a large and complicated multiplication example: 12305 x 5641. We will stick to the rules we learned earlier.
First, write down the expression in column
Now start multiplying. The number 12305 must be multiplied by each digit of the number 5641.
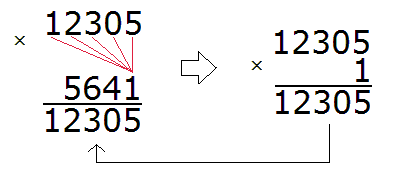
By multiplying 12305 by 1, we get 12305 and write this number so that the unit digit of this number is below the unit by which we multiplied 12305.
Now we multiply 12305 by the next digit 4:
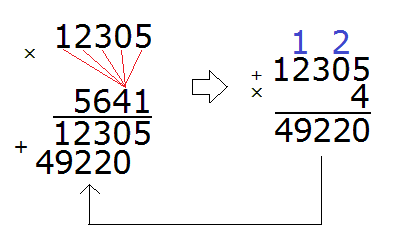
We multiply 12305 by the next number 6:
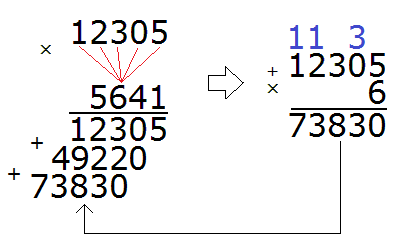
By multiplying 12305 by 6, we get 73830, and we write this number down so that the unit digit of this number is below the six by which we multiplied 12305.
Now multiply 12305 by the last digit of 5:
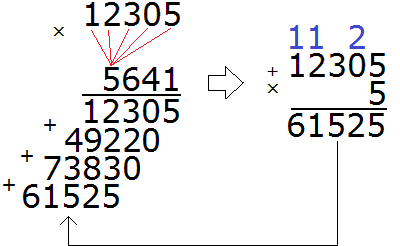
By multiplying 12305 by 5, we got 61525, and we wrote down this number so that the unit digit of this number is under the five by which we multiplied 12305.
The result is a large ladder, which must be added up. We add up:
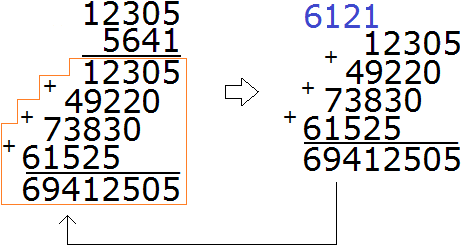
The final answer is 69412505.
If you understood this example, we can say that you learned multiplication of large numbers very well.
That concludes the lesson on multiplication. Be sure to practice by solving some of the examples given below.
It is important to note that it is not customary to draw all these arrows and detailed solutions as in pictures in "combat conditions". You need to be able to write down the answers right away, doing all the calculations in your mind.
The exception is if a person hasn't done math for a long time or has never done math before. In this case, you can draw arrows and other auxiliary diagrams for a good assimilation of the material.
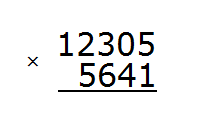
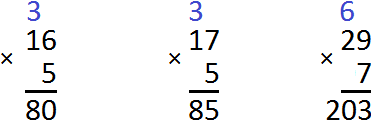
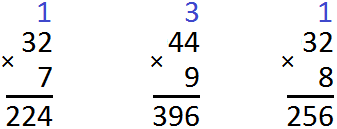
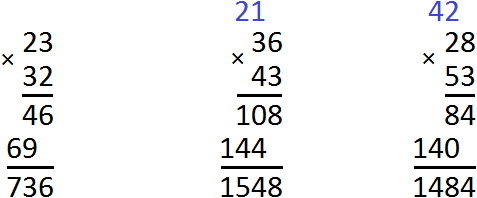
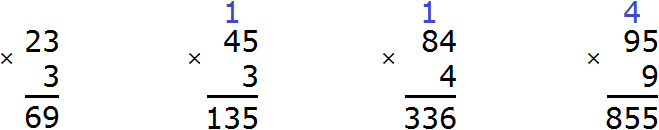
Comments