We have already said that fractions can be regular and decimal. At this point, we've learned a little bit about regular fractions. We have learned that fractions can be proper or improper. We also learned that fractions can be simplified, added, subtracted, multiplied, and divided. We also learned that there are so-called mixed numbers which consist of whole and fractional parts.
We haven't fully explored common fractions yet. There are many subtleties and details to talk about, but today we will begin to study decimals, since ordinary and decimal fractions quite often have to be combined. That is, you have to work with both kinds of fractions when solving problems.
This lesson may seem complicated and incomprehensible. This is quite normal. These kinds of lessons require that they be studied, not looked at superficially.
Expressing values as fractions
Sometimes it is convenient to show something in fractional form. For example, one tenth of a decimeter is written like this:
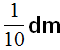
This expression means that one decimeter was divided into ten equal parts, and one part was taken from those ten parts. And one part of ten in this case is equal to one centimeter:
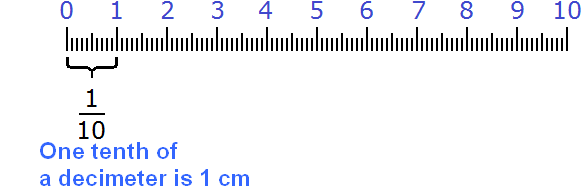
Consider the following example. Suppose we need to show 6 cm and another 3 mm in centimeters in fractional form.
So we already have 6 whole centimeters:

But there are still 3 millimeters left. How do you show these 3 millimeters in centimeters? Fractions come to the rescue. One centimeter is ten millimeters. Three millimeters is three parts of ten. And three parts of ten are written as ![]() cm
cm
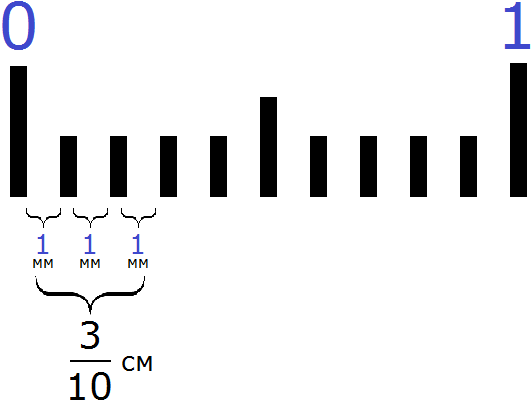
The expression ![]() cm means that one centimeter was divided into ten equal parts, and three parts were taken from these ten parts.
cm means that one centimeter was divided into ten equal parts, and three parts were taken from these ten parts.
The result is six whole centimeters and three tenths of a centimeter:
![]()
The number 6 indicates the number of whole centimeters, and the fraction ![]() indicates the number of fractions. This fraction reads "six whole and three tenths centimeters".
indicates the number of fractions. This fraction reads "six whole and three tenths centimeters".
Fractions with numbers 10, 100, 1000 in the denominator can be written without a denominator. First write the whole part and then the numerator of the fractional part. The whole part is separated from the numerator of the fractional part by a decimal point.
For example, write down ![]() without the denominator. First we write down the whole part. The whole part is 6
without the denominator. First we write down the whole part. The whole part is 6
6
The whole part is written down. Immediately after writing the whole part, put a dot:
6.
And now write down the numerator of the fractional part. In the mixed number ![]() , the numerator of the fractional part is 3. Write a 3 after the decimal point:
, the numerator of the fractional part is 3. Write a 3 after the decimal point:
6.3
Any number that is represented in this form is called a decimals.
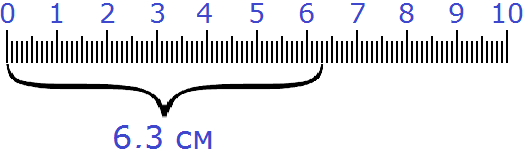
Therefore, you can show 6 cm and another 3 mm in centimeters with a decimal:
6.3 cm
It will look like this:
In fact, decimals are the same as regular fractions and mixed numbers. The peculiarity of such fractions is that the denominator of their fractional part contains numbers 10, 100, 1000 or 10000.
Like a mixed number, a decimal has a whole part and a fractional part. For example, in the mixed number ![]() , the whole part is 6 and the fractional part is
, the whole part is 6 and the fractional part is ![]() .
.
In the decimal 6.3, the whole part is the number 6, and the fractional part is the numerator of the fraction ![]() , that is, the number 3.
, that is, the number 3.
It also happens that ordinary fractions with numbers 10, 100, 1000 in the denominator are given without a whole part. For example, the fraction ![]() is given without the whole part. To write such a fraction as a decimal, first write 0, then put a decimal point and write the numerator of the fractional part. The fraction
is given without the whole part. To write such a fraction as a decimal, first write 0, then put a decimal point and write the numerator of the fractional part. The fraction ![]() without the denominator would be written as follows:
without the denominator would be written as follows:
0,5
It reads "zero point five".
Converting mixed numbers to decimals
When we write mixed numbers without a denominator, we convert them to decimals. When converting regular fractions into decimals, there are a few things we need to know, which we will talk about in a moment.
After the whole part is written, be sure to count the number of zeros in the denominator of the fractional part, because the number of zeros in the fractional part and the number of digits after the decimal point in the decimal must be the same. What does this mean? Consider the following example: Convert the mixed number ![]() into a decimal.
into a decimal.
First write down the whole part and put a dot:
3.
And you could immediately write down the numerator of the fractional part and the decimal is ready, but you have to count how many zeros are contained in the denominator of the fractional part.
So, let's calculate the number of zeroes in the fractional part of the mixed number ![]() . We see that the denominator of the fractional part is one zero. So the decimal will have one digit after the decimal point, and this digit will be the numerator of the fractional part of the mixed number
. We see that the denominator of the fractional part is one zero. So the decimal will have one digit after the decimal point, and this digit will be the numerator of the fractional part of the mixed number ![]() , that is, the number 2
, that is, the number 2
3.2
Thus, the mixed number ![]() when converted to a decimal is converted to 3.2. This decimal is read as follows:
when converted to a decimal is converted to 3.2. This decimal is read as follows:
«Three point two-tenths»
"Tenths" because the fractional part of the mixed number ![]() contains the number 10.
contains the number 10.
Example 2. Convert the mixed number ![]() into a decimal.
into a decimal.
Write down the whole part and put a dot:
5.
And we could just write the numerator of the fractional part and get a decimal 5.3, but the rule says that there must be as many digits after the decimal point as there are zeroes in the denominator of the fractional part of a mixed number ![]() . And we see that there are two zeros in the denominator of the fractional part of
. And we see that there are two zeros in the denominator of the fractional part of ![]() . So our decimal must have two digits after the decimal point, not one.
. So our decimal must have two digits after the decimal point, not one.
In such cases, the numerator of the fractional part should be slightly modified: add a zero before the numerator, that is, before the number 3
![]()
Now you can finish the job. Write the numerator of the fractional part after the decimal point:
5.03
We see that the number of digits after the point and the number of zeroes in the denominator of the fractional part of the mixed ![]() number are the same.
number are the same.
The decimal 5.03 reads like this:
«Five point three hundredths»
"Hundredths" because the denominator of the fractional part of the mixed number ![]() contains the number 100.
contains the number 100.
Example 3. Convert the mixed number ![]() into a decimal.
into a decimal.
From the previous examples, we learned that to successfully convert a mixed number to a decimal, the number of digits in the numerator fractional part and the number of zeros in the denominator fractional part must be the same.
Before converting a mixed ![]() number into a decimal, its fractional part should be slightly modified, namely, to make the number of digits in the numerator fractional part and the number of zeroes in the denominator fractional part be the same.
number into a decimal, its fractional part should be slightly modified, namely, to make the number of digits in the numerator fractional part and the number of zeroes in the denominator fractional part be the same.
First, we look at the number of zeros in the denominator of the fractional part. We see that there are three zeros:
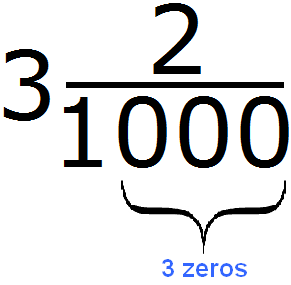
Our task is to organize three digits in the numerator of the fractional part. We already have one digit - the digit 2. We need to add two more digits. They are two zeros. We add them before number 2. As a result, the number of zeros in the denominator and the number of digits in the numerator will be the same:

Now you can do the translation of this mixed number into a decimal. First write down the whole part and put a dot:
3.
and immediately write the numerator of the fractional part
3.002
We see that the number of digits after the decimal point and the number of zeroes in the denominator of the fractional part of the mixed ![]() number are the same.
number are the same.
The decimal 3.002 reads like this:
«Three point two thousandths»
"Thousands" because the denominator of the fractional part of a mixed ![]() number contains the number 1000.
number contains the number 1000.
Converting fractions to decimal
Ordinary fractions with 10, 100, 1000 or 10000 in the denominator can also be converted to decimals. Since a fraction has no whole part, first write down 0, then put a dot and write down the numerator of the fractional part.
Here too, the number of zeros in the denominator and the number of digits in the numerator must be the same. Therefore, you should be careful.
Example 1. Convert an ordinary fraction ![]() into a decimal.
into a decimal.
The whole part is missing, so first write 0 and put a dot:
0.
Now look at the number of zeros in the denominator. We see that there is one zero. And there is one digit in the numerator. So we can safely continue the decimal by writing the number 5 after the point
0.5
In the resulting 0.5 decimal, the number of digits after the dot and the number of zeroes in the denominator of the fraction ![]() are the same. So the fraction is converted correctly.
are the same. So the fraction is converted correctly.
The decimal 0.5 reads like this:
«Zero point five»
Example 2. Convert an ordinary fraction ![]() into a decimal.
into a decimal.
The whole part is missing. Write 0 first and put a dot:
0.
Now look at the number of zeros in the denominator. We see that there are two zeros. And there is only one digit in the numerator. To make the number of digits and the number of zeros the same, we add one zero before number 2 in the numerator. Then the fraction will look like ![]() . Now the number of zeros in the denominator and the number of digits in the numerator are the same. So we can continue the decimal:
. Now the number of zeros in the denominator and the number of digits in the numerator are the same. So we can continue the decimal:
0.02
In the resulting decimal 0.02, the number of digits after the point and the number of zeroes in the denominator of the fraction ![]() are the same. So the fraction is translated correctly.
are the same. So the fraction is translated correctly.
The decimal 0.02 reads like this:
«Zero point two hundredths».
Example 3. Convert an ordinary fraction ![]() into a decimal.
into a decimal.
Write 0 and put a dot:
0.
Now count the number of zeroes in the denominator of the fraction ![]() . We see that there are five zeros, and only one digit in the numerator. To make the number of zeros in the denominator and the number of digits in the numerator the same, we need to add four zeros before the number 5 in the numerator:
. We see that there are five zeros, and only one digit in the numerator. To make the number of zeros in the denominator and the number of digits in the numerator the same, we need to add four zeros before the number 5 in the numerator:
![]()
Now you can continue the decimal. Write the numerator of the fraction ![]() after the point
after the point
0.00005
In the resulting decimal 0.00005, the number of digits after the decimal point and the number of zeroes in the denominator of the fraction ![]() are the same. So the fraction is converted correctly.
are the same. So the fraction is converted correctly.
The decimal 0.00005 reads like this:
«Zero point five one hundred thousand».
Conversion of improper fractions to decimal
An improper fraction is a fraction with a numerator greater than the denominator.
There are improper fractions that have 10, 100, 1000 or 10000 in the denominator. Such fractions can be converted to decimals. However, before converting to a decimal, the whole part of the fraction must be extracted.
Example 1. Convert an improper fraction ![]() into a decimal.
into a decimal.
Fraction ![]() is an improper fraction. To convert such a fraction into a decimal, you must first select the whole part of the fraction. Recall how to select the whole part of improper fractions. If you forget, we suggest that you go back to this topic and study it thoroughly.
is an improper fraction. To convert such a fraction into a decimal, you must first select the whole part of the fraction. Recall how to select the whole part of improper fractions. If you forget, we suggest that you go back to this topic and study it thoroughly.
So, let us distinguish the whole part in the improper fraction ![]() . Recall that a fraction means division, in this case dividing 112 by 10. The division must be done with a remainder:
. Recall that a fraction means division, in this case dividing 112 by 10. The division must be done with a remainder:
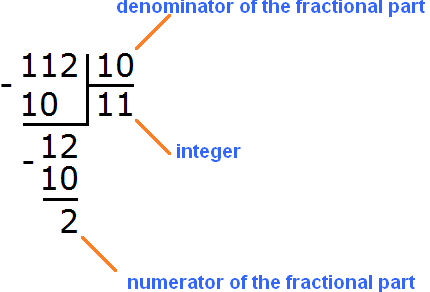
Let's look at this picture and assemble a new mixed number, like a children's construction set. The quotient 11 is the whole part, the remainder 2 is the numerator of the fractional part, and the divisor 10 is the denominator of the fractional part:
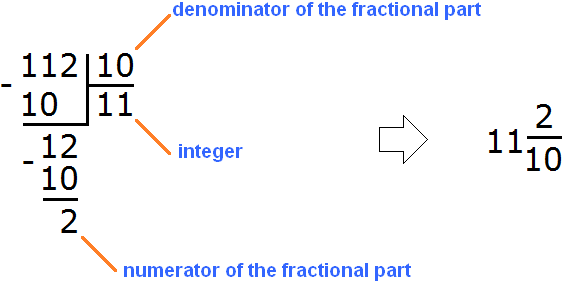
We got a mixed number of ![]() . We will convert it to a decimal. And we already know how to convert such numbers to decimals. First, we write down the whole part and put a dot:
. We will convert it to a decimal. And we already know how to convert such numbers to decimals. First, we write down the whole part and put a dot:
11.
Now count the number of zeros in the denominator of the fractional part. We see that there is one zero. And there is one digit in the numerator of the fractional part. So the number of zeros in the denominator of the fractional part and the number of digits in the numerator of the fractional part are the same. This allows us to write the numerator of the fractional part right after the point:
11.2
So the wrong fraction ![]() when converted to decimal converts to 11.2
when converted to decimal converts to 11.2
The decimal 11.2 reads like this:
«Eleven point two-twenty».
Example 2. Convert an improper fraction ![]() into a decimal.
into a decimal.
This is an improper fraction because the numerator is larger than the denominator. But it can be converted to a decimal because the denominator contains the number 100.
First of all, isolate the whole part of this fraction. To do this, divide 450 by 100:
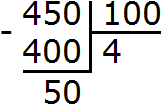
Let's put together a new mixed number - we get ![]() . Now convert it to a decimal. Write down the whole part and dot it:
. Now convert it to a decimal. Write down the whole part and dot it:
4.
Now count the number of zeros in the denominator of the fractional part and the number of digits in the numerator of the fractional part. We see that the number of zeros in the denominator and the number of digits in the numerator are the same. This allows us to write the numerator of the fractional part after the dot:
4.50
So the wrong fraction ![]() when converted to decimal converts to 4.50
when converted to decimal converts to 4.50
When solving problems, if there are zeros at the end of a decimal, they can be discarded. Let's discard the zero in our answer, too. Then we get 4.5
This is one of the interesting features of decimals. It consists in the fact that zeros that stand at the end of the fraction do not give any weight to the fraction. In other words, the decimal 4.50 and 4.5 are equal and you can put an equal sign between them:
4.50 = 4.5
This begs the question, "Why is this the case?" After all, 4.50 and 4.5 look different fractions. The whole secret lies in the basic property of fractions, which we studied earlier. We will try to prove why the decimals 4.50 and 4.5 are equal, but after studying the next topic, which is called "converting a decimal to a mixed number".
Converting decimals to mixed numbers
Any decimal can be converted back to a mixed number. To do this, all you need to know is how to read decimals.
For example, let's convert 6.3 to a mixed number. 6.3 is six integers and three tenths. Let's write down six integers first:
6
and next to three tenths:
![]()
Example 2. Convert a decimal 3.002 to a mixed number
3.002 is three integers and two thousandths. We first write down three integers
3
and next to it write down two thousandths:
3 ![]()
Example 3. Convert a decimal 4.50 to a mixed number
4.50 is four whole and fifty hundredths. Write down four integers
4
and next to fifty hundredths:
![]()
By the way, let's recall the last example from the previous thread. We said that the decimals 4.50 and 4.5 are equal. We also said that zero can be discarded. Let us prove that decimals 4.50 and 4.5 are equal. To do this, convert both decimals to mixed numbers.
After converting to a mixed number, the decimal 4.50 is converted to ![]() , and the decimal 4.5 is converted to
, and the decimal 4.5 is converted to ![]()
We have two mixed numbers ![]() and
and ![]() . Convert these mixed numbers into improper fractions:
. Convert these mixed numbers into improper fractions:
![]()
![]()
Now we have two fractions ![]() and
and ![]() . Now remember the basic property of fractions, which says that when you multiply (or divide) the numerator and denominator of a fraction by the same number, the value of the fraction does not change.
. Now remember the basic property of fractions, which says that when you multiply (or divide) the numerator and denominator of a fraction by the same number, the value of the fraction does not change.
Let's divide the numerator and denominator of the first fraction ![]() by the number 10
by the number 10
![]()
We got ![]() , and this is the second fraction. So
, and this is the second fraction. So ![]() and
and ![]() are equal to each other and equal to the same value:
are equal to each other and equal to the same value:
![]() =
= ![]()
Try using a calculator to first divide 450 by 100 and then 45 by 10. It's a funny thing to do.
Converting decimal to fractions
Any decimal can be converted back to a regular fraction. Again, to do this, it is enough to know how to read decimals. For example, translate 0.3 into an ordinary fraction. 0.3 is zero point three. Write down zero integers first:
0
and next to three tenths 0![]() . Zero is traditionally not written down, so the final answer is not 0
. Zero is traditionally not written down, so the final answer is not 0![]() , but just
, but just ![]() .
.
Example 2. Convert a decimal 0.02 into an ordinary fraction.
0.02 is zero integers and two hundredths. We do not write down zero, so we write down two hundredths
![]()
Example 3. Convert 0.00005 to a fraction
0.00005 is zero integers and five hundred thousandths. We do not write down zero, so we immediately write down five hundred thousandths
![]()
Example 4. Convert 3.5 to a fraction
First, convert the given decimal to a mixed number:
![]()
Now convert the mixed number ![]() to an improper fraction:
to an improper fraction:
![]()
Example 5. Convert 1.25 to a fraction
First, convert the given decimal to a mixed number:
![]()
Now convert the mixed number ![]() to an improper fraction:
to an improper fraction:
![]()
Comments