We know that if we want to convert a mixed number into an improper fraction, we need to multiply the integer part by the denominator of the fractional part and add it to the numerator of the fractional part. The resulting number will be the numerator of the new fraction, and the denominator remains the same.
For example, let's convert the mixed number ![]() to an improper fraction
to an improper fraction
Multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part:
(2 × 2) + 1
Let's calculate this expression:
(2 × 2) + 1 = 4 + 1 = 5
The resulting number 5 will be the numerator of the new fraction, and the denominator will remain the same:
![]()
This procedure is written in full as follows:
![]()
To return the original mixed number, just highlight the integer part in the fraction ![]()
![]()
But this method of converting a mixed number into an improper fraction is applicable only if the mixed number is positive. For a negative number, this method will not work.
Consider the fraction ![]() . We distinguish the integer part of the fraction. We get
. We distinguish the integer part of the fraction. We get ![]()
![]()
To return the original fraction ![]() , we need to convert the mixed number
, we need to convert the mixed number ![]() into an improper fraction. But if we use the old rule, which is to multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part to the resulting number, we get the following contradiction:
into an improper fraction. But if we use the old rule, which is to multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part to the resulting number, we get the following contradiction:
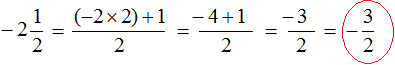
We got a fraction of ![]() , and we should have gotten a fraction of
, and we should have gotten a fraction of ![]() .
.
We conclude that the mixed number ![]() is incorrectly converted into an improper fraction:
is incorrectly converted into an improper fraction:
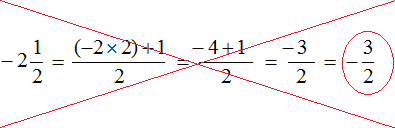
To convert a negative mixed number into an improper fraction correctly, multiply the integer part by the denominator of the fractional part, and subtract the numerator of the fractional part from the resulting number. In this case, everything will fall into place
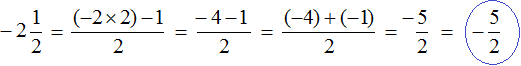
The negative mixed number ![]() is the opposite of the mixed number
is the opposite of the mixed number ![]() . If the positive mixed number
. If the positive mixed number ![]() is on the right side and looks like this
is on the right side and looks like this

then the negative mixed number ![]() will be located in the left part symmetrically
will be located in the left part symmetrically ![]() relative to the origin
relative to the origin

And while ![]() reads "two integers and one second,"
reads "two integers and one second," ![]() reads "minus two and a half". Because the numbers -2 and
reads "minus two and a half". Because the numbers -2 and ![]() are on the left side of the coordinate line, they are both negative.
are on the left side of the coordinate line, they are both negative.
Any mixed number can be written in expanded form. A positive mixed number ![]() is written as
is written as ![]() in expanded form.
in expanded form.
And a negative mixed number ![]() is written as
is written as ![]()
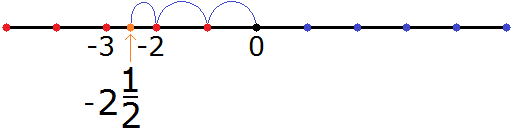
Now we can understand why the mixed number ![]() is located on the left side of the number line. The minus before the two indicates that we moved from zero two steps to the left, as a result we are at the point where the number -2
is located on the left side of the number line. The minus before the two indicates that we moved from zero two steps to the left, as a result we are at the point where the number -2
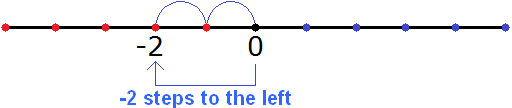
Then, starting from the number -2, we move another ![]() step to the left. And since the value of
step to the left. And since the value of ![]() is -0.5, our step is half of the full step.
is -0.5, our step is half of the full step.

We end up in the middle between the numbers -3 and -2
Example 2. Select the integer part of an improper fraction ![]() , then convert the resulting mixed number back to an improper fraction
, then convert the resulting mixed number back to an improper fraction
Let's do the first part of the assignment, namely, isolate the integer part in the improper fraction ![]()
![]()
Perform the second part of the problem, namely, convert the resulting mixed number ![]() to an improper fraction. To do this, multiply the integer part by the denominator of the fractional part and subtract the numerator of the fractional part from the resulting number:
to an improper fraction. To do this, multiply the integer part by the denominator of the fractional part and subtract the numerator of the fractional part from the resulting number:
![]()
If you don't want to get confused and get used to the new rule, you can put the mixed number in parentheses and leave the minus behind the parentheses. Then you can apply the good old rule: multiply the integer part by the denominator of the fractional part and add the numerator of the fractional part to the resulting number.
Let's perform the previous task in this way, namely, to convert the mixed number ![]() into an improper fraction
into an improper fraction
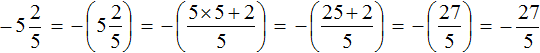
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.