Algebraic expressions are an expressions built up from integer constants, variables, and the algebraic operations.
For example, the following expression is a algebraic expression:
a + b + 4
You can use algebraic expressions to write laws, formulas, equations. The ability to manipulate algebraic expressions is the key to a good knowledge of algebra and higher mathematics.
Any serious problem in math comes down to solving equations. And to be able to solve equations, you need to be able to work with algebraic expressions.
To work with algebraic expressions, you need to learn basic arithmetic: addition, subtraction, multiplication, division, the basic laws of mathematics, fractions, actions with fractions, and proportions. And not just learn, but understand thoroughly.
Variables
The letters that are contained in algebraic expressions are called variables.
For example, in the expression a + b + 4, the letters a and b are variables. If any numbers are substituted for these variables, the algebraic expression a + b + 4 will turn into a numeric expression whose value can be found.
Numbers that are substituted for variables are called variable values.
Variable value - a constant, which is a number that is expressed as.
For example, change the values of variables a and b. The equals sign is used to replace variables by their values.
a = 2, b = 3
The variable a has been assigned a value of 2, and the variable b has been assigned a value of 3. As a result, the algebraic expression a + b + 4 turns into the usual numeric expression 2 + 3 + 4, the value of which can be found:
2 + 3 + 4 = 9
When variables are multiplied, they are written together.
For example, writing ab means the same thing as writing a × b. If we substitute numbers 2 and 3 for variables a and b, we get 6
2 × 3 = 6
You can also write the multiplication of a number by an expression in parentheses.
For example, instead of a × (b + c) you can write a(b + c). Applying the distributive law of multiplication, we obtain a(b + c) = ab + ac.
Coefficients
In algebraic expressions, you often see a notation where a number and a variable are written together, such as '3a'. This is actually a short notation of multiplying the number 3 by the variable a and this notation looks like 3 × a.
In other words, the expression 3a is the product of the number 3 and the variable a. The number 3 in this product is called the coefficient. This coefficient shows how many times the variable a will be increased. This expression can be read as " three times 'a' ", or "increase the value of 'a' three times".
For example, if the variable a is 5, then the value of the expression 3a is 15.
3 × 5 = 15
Simply put, a quotient is a number in front of a variable (in front of a letter).
There can be several variables, for example 5abc. Here the coefficient is the number 5. This coefficient shows that the product of the variables abc increases by five. This expression can be read as "five times abc".
If we substitute numbers 2, 3, and 4 for the variables abc, then the value of the expression 5abc will be 120
5 × 2 × 3 × 4 = 120
You can mentally imagine first multiplying the numbers 2, 3, and 4, and the resulting value multiplied by a factor of five:
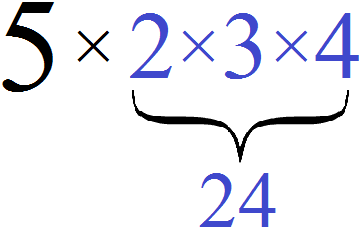
The coefficient sign refers only to the coefficient, and does not refer to variables!
Consider the expression -6b. The minus in front of the coefficient 6 refers only to the coefficient 6, and does not refer to the variable b. Understanding this fact will help you not to make mistakes with signs in the future.
Example 1. Find the value of the expression -6b when b = 3.
-6b is a short form of -6 × b. For clarity, let us write the expression -6b in expanded form and substitute the value of the variable b
−6b = −6 × b = −6 × 3 = −18
Example 2. Find the value of the expression -6b when b = -5
Let us write the expression -6b in expanded form
−6b = −6 × b
and then substitute the value of the variable b
−6b = −6 × b = −6 × (−5) = 30
Example 3. Find the value of the expression -5a + b if a = 3 and b = 2
-5a + b is a short form of -5 × a + b, so for clarity we write the expression -5 × a + b in expanded form and substitute the values of the variables a and b
−5a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13
Sometimes variables are written without a coefficient, for example a or ab. In this case the coefficient is 1:
1a, 1ab
but the one is usually not written down, so they just write a or ab.
If the variable is preceded by a minus, the coefficient is the number -1.
For example, the expression -a actually looks like -1a. It is the product of minus one and the variable a. It is obtained as follows:
−1 × a = −1a
There is a small catch here. In the -a expression, the minus in front of the a variable actually refers to the invisible unit, not to the a variable. So you should be careful when solving problems.
For example, if an expression -a is given and we are asked to find its value for a = 2, at school we used to substitute two for the variable a and got the answer -2, not really thinking about how it happened. In fact, we multiplied minus one by the positive number 2.
−a = −1 × a
−1 × a = −1 × 2 = −2
If an expression -a is given and we want to find its value for a = -2, we substitute -2 for the variable a
−a = −1 × a
−1 × a = −1 × (−2) = 2
To avoid mistakes, the first time invisible units can be written explicitly.
Example 4. Evaluate the expression abc for a=2, b=3 and c=4
The expression abc is a short form of 1×a×b×c. For clarity, let us write abc in expanded form and substitute values of variables a, b, and c
1 × a × b × c = 1 × 2 × 3 × 4 = 24
Example 5. Evaluate the expression abc for a=-2, b=-3 and c=-4
Write the expression abc in expanded form and substitute the values of the variables a, b, and c
1 × a × b × c = 1 × (−2) × (−3) × (−4) = −24
Example 6. Evaluate the expression -abc for a=3, b=5, and c=7
The expression -abc is a short form of -1×a×b×c. For clarity, write the expression -abc in expanded form and substitute the values of the variables a, b and c
−abc = −1 × a × b × c = −1 × 3 × 5 × 7 = −105
Example 7. Evaluate the expression -abc for a=-2, b=-4 and c=-3
Write the expression -abc in expanded form:
−abc = −1 × a × b × c
Let's substitute the values of the variables a, b, and c
−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24
How to calculate the coefficient
Sometimes you need to solve a problem in which you want to calculate the coefficient of an expression. In principle, this problem is very simple. It is enough to know how to multiply numbers correctly.
To calculate the quotient of an expression, multiply the numbers in the expression separately and multiply the variables separately. The resulting numerical multiplier will be the coefficient.
Example 1. Calculate the coefficient in the expression: 7m×5a×(-3)×n
An expression consists of several factors. This can be clearly seen if we write the expression in expanded form. That is, write the products 7m and 5a in the form 7×m and 5×a
7 × m × 5 × a × (−3) × n
Apply the associative law of multiplication, which allows us to multiply the multipliers in any order. Namely, multiply numbers separately and multiply letters (variables) separately:
−3 × 7 × 5 × m × a × n = −105man
The coefficient is equal to -105. After completion, it is desirable to arrange the variable part in alphabetical order:
−105amn
Example 2. Calculate the coefficient in the expression: -a×(-3)×2
Let's multiply the numbers and variables separately:
−a × (−3 ) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a
The coefficient is 6.
Example 3. Calculate the coefficient in the expression: ![]()
Let's multiply the numbers and variables separately:
![]()
The coefficient is equal to -1. Note that the one is not written, because it is customary not to write the coefficient 1.
These seemingly simple tasks can play a very cruel trick on us. Often it turns out that the sign of the quotient is wrong: either a minus sign is missing or, on the contrary, it is put there in vain. To avoid these unfortunate mistakes, the topic of multiplication of integers must be studied at a good level.
The summands in algebraic expressions
When you add several numbers, you get the sum of the numbers. The numbers that are added are called summands. There may be more than one summand, for example:
1 + 2 + 3 + 4 + 5
When an expression consists of summands, it is much easier to calculate because adding is easier than subtracting. But an expression may contain not only addition but also subtraction, for example:
1 + 2 − 3 + 4 − 5
In this expression, the numbers 3 and 5 are subtractors, not summands. But nothing prevents us from replacing subtraction with addition. Then we again get an expression consisting of summands:
1 + 2 + (−3) + 4 + (−5)
It does not matter that the numbers -3 and -5 now have a minus sign. The main thing is that all the numbers in this expression are connected by an addition sign, that is, the expression is a sum.
Both expressions 1 + 2 - 3 + 4 - 5 and 1 + 2 + (-3) + 4 + (-5) are equal to the same value - minus one:
1 + 2 − 3 + 4 − 5 = −1
1 + 2 + (−3) + 4 + (−5) = −1
Thus, the value of the expression will not be affected if we substitute addition for subtraction somewhere.
You can also substitute addition for subtraction in algebraic expressions. For example, consider the following expression:
7a + 6b − 3c + 2d − 4s
Replace subtraction with addition where possible:
7a + 6b + (−3c) + 2d + (−4s)
For any value of the variables a, b, c, d, and s, the expressions 7a + 6b - 3c + 2d - 4s and 7a + 6b + (-3c) + 2d + (-4s) will equal the same value.
You should be prepared for the fact that a teacher at school or a teacher at an institute may call even those numbers (or variables) that are not addends.
For example, if the difference a - b is written on the board, the teacher will not say that a is the minuend and b is the subtrahend. He will call both variables by one common word - addends. This is because the mathematician sees an expression of the form a - b as the sum of a + (-b). In this case, the expression becomes a sum, and the variables a and (-b) become addends.
Like terms
Like terms (Similar Terms) are terms that have the same variables.
For example, consider the expression 7a + 6b + 2a. The summands 7a and 2a have same variables - the variable a. So the summands 7a and 2a are like.
Usually, like terms are added to simplify an expression or to solve an equation. This action is called a combining like terms.
To combine like terms, sum all coefficients of these terms, and multiply the result by the same variable part.
For example, combine like terms in the expression 3a + 4a + 5a. In this case all the summands are like. Add their coefficients and multiply the result by the common variable part - by the variable a
3a + 4a + 5a = (3 + 4 + 5)×a = 12a
Such terms are usually combined in the mind and the result is written down at once:
3a + 4a + 5a = 12a
Also, you can reason as follows:
There were 3 variables a, added 4 more variables a and 5 more variables a. The result was 12 variables a
Let's look at some examples on combining like terms. Given that this topic is very important, at first we will write down every detail in detail. Despite the fact that everything here is very simple, most people make a lot of mistakes. Mostly through inattention rather than ignorance.
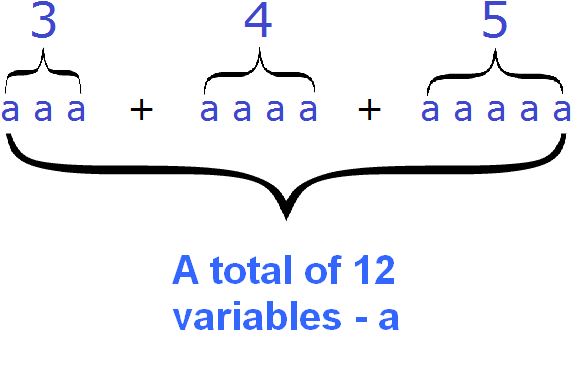
Example 1. Combine like terms in the expression 3a + 2a + 6a + 8a
Add the coefficients in this expression and multiply the result by the same variable part:
3a + 2a + 6a + 8a= (3 + 2 + 6 + 8) × a = 19a
The construction (3 + 2 + 6 + 8) × a may not be written down, so we write down the answer immediately
3a + 2a + 6a + 8a = 19a
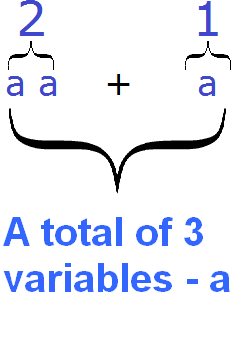
Example 2. Combine like terms in the expression 2a + a
The second summand a is written without a coefficient, but in fact it is preceded by a coefficient of 1, which we do not see because it is not written down. Therefore, the expression looks as follows:
2a + 1a
Now let's combine like terms. That is, add up the coefficients and multiply the result by the total variable part:
2a + 1a = (2 + 1) × a = 3a
Let's write down the solution shortly:
2a + a = 3a
Combining like terms in the expression 2a+a, it is possible to reason in a different way:
There were 2 variables a, we added another variable a, so we ended up with 3 variables a.
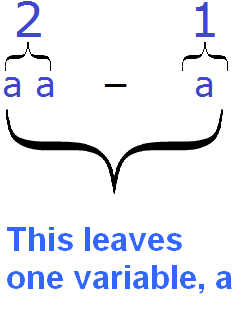
Example 3. Combine like terms in the expression 2a − a
Replace subtraction with addition:
2a + (−a)
The second term (-a) is written without a coefficient, but it actually looks like (-1a). The coefficient -1 is again invisible because it is not written down. Hence, the expression looks like this:
2a + (−1a)
Now let's combine like terms. Add up the coefficients and multiply the result by the equal variable part:
2a + (−1a) = (2 + (−1)) × a = 1a = a
Usually they write it down shorter:
2a − a = a
Combining like terms in the expression 2a−a, it is possible to reason in a different way:
There were 2 variables a, subtracted one variable a, leaving one single variable a
Example 4. Combine like terms in the expression 6a − 3a + 4a − 8a
Replace subtraction with addition where possible:
6a − 3a + 4a − 8a = 6a + (−3a) + 4a + (−8a)
Now let's combine like terms. Add up the coefficients and multiply the result by the equal variable part
(6 + (−3) + 4 + (−8)) × a = −1a = −a
Let's write down the solution shortly:
6a − 3a + 4a − 8a = −a
There are expressions that contain several different like terms.
For example, 3a + 3b + 7a + 2b. The same rules are valid for such expressions as for the others, namely, adding the coefficients and multiplying the result by the common variable part. But to avoid mistakes, it is convenient to underline different groups of summands with different lines.
For example, in the expression 3a + 3b + 7a + 2b, those terms that contain the variable a can be underlined with one line, and those terms that contain the variable b can be underlined with two lines:
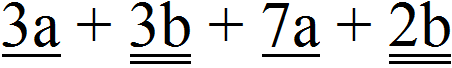
Now let's combine like terms. That is, add up the coefficients and multiply the result by the common variable part. Do this for both groups of summands: for the summands containing variable a and for the summands containing variable b.
3a + 3b + 7a + 2b = (3+7)×a + (3 + 2)×b = 10a + 5b
Again, the expression is uncomplicated, and like terms can be combined in the mind:
3a + 3b + 7a + 2b = 10a + 5b
Example 5. Combine like terms in the expression 5a − 6a −7b + b
Replace subtraction with addition where possible:
5a − 6a −7b + b = 5a + (−6a) + (−7b) + b
Let's underline like terms with different lines. Underline the terms containing variables a with one line, and underline the terms containing variables b with two lines:
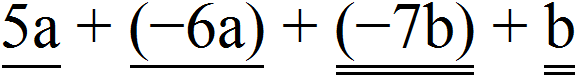
Now let's combine like terms. Add up the coefficients and multiply the result by the common variable part:
5a + (−6a) + (−7b) + b = (5 + (−6))×a + ((−7) + 1)×b = −a + (−6b)
If the expression contains regular numbers without any variable factors, they are added separately.
Example 6. Combine like terms in the expression 4a + 3a − 5 + 2b + 7
Replace subtraction with addition where possible:
4a + 3a − 5 + 2b + 7 = 4a + 3a + (−5) + 2b + 7
Now let's combine like terms. The numbers -5 and 7 have no literal factors, but they are like terms - you just have to add them up. And the term 2b will remain unchanged because it is the only term in the expression that has a literal factor b, and there is nothing to add it to:
4a + 3a + (−5) + 2b + 7 = (4 + 3)×a + 2b + (−5) + 7 = 7a + 2b + 2
Let's write down the solution shortly:
4a + 3a − 5 + 2b + 7 = 7a + 2b + 2
The terms can be ordered so that those terms that have the same variable part are in the same part of the expression.
Example 7. Combine like terms in the expression 5t+2x+3x+5t+x
Since an expression is a sum of several terms, this allows us to calculate it in any order. Therefore, we can write the terms containing the variable t at the beginning of the expression, and the terms containing the variable x at the end of the expression:
5t + 5t + 2x + 3x + x
It is now possible to combine like terms:
5t + 5t + 2x + 3x + x = (5+5)×t + (2+3+1)×x = 10t + 6x
Let's write down the solution shortly:
5t + 2x + 3x + 5t + x = 10t + 6x
The sum of the opposite numbers is zero. This rule works for algebraic expressions as well. If an expression contains identical summands, but with opposite signs, you can get rid of them at the stage of combining the like terms. In other words, simply cross them out of the expression, since their sum is zero.
Example 8. Combine like terms in the expression 3t − 4t − 3t + 2t
Replace subtraction with addition where possible:
3t − 4t − 3t + 2t = 3t + (−4t) + (−3t) + 2t
The terms 3t and (-3t) are opposite. The sum of the opposite terms is zero. If we remove this zero from the expression, the value of the expression will not change, so we will remove it. And we remove it by simply crossing out the summands 3t and (-3t)
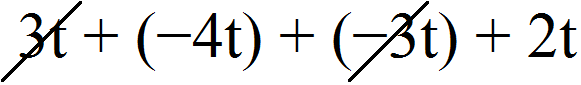
As a result, we are left with the expression (-4t) + 2t. In this expression we can combine like terms and get the final answer:
(−4t) + 2t = ((−4) + 2)×t = −2t
Let's write down the solution shortly:
![]()
Simplifying expressions
Often you will see an assignment that says "simplify an expression" and then gives the expression you want to simplify. Simplify an expression means to make it simpler and shorter.
In fact, we were already simplifying expressions when we reduced fractions. After reduction, the fraction becomes shorter and easier to understand.
Consider the following example. Simplify the expression ![]() .
.
This assignment can literally be understood as: "Apply any possible actions to this expression, but make it simpler".
In this case, you can reduce the fraction, namely, divide the numerator and denominator of the fraction by 2:
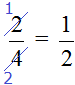
What else can be done? We can calculate the resulting fraction ![]() . Then we get a decimal of 0.5
. Then we get a decimal of 0.5
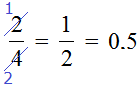
As a result, the fraction ![]() was simplified to 0.5.
was simplified to 0.5.
The first question you should ask yourself when dealing with tasks like this should be: "what can be done?" Because there are actions that can be done, and there are actions that cannot be done.
Another important thing to keep in mind is that the value of the expression must not change after simplifying the expression. Let's return to the expression ![]() . This expression is a division that can be performed. By performing this division, we get the value of this expression, which is 0.5
. This expression is a division that can be performed. By performing this division, we get the value of this expression, which is 0.5
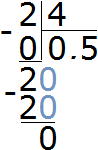
But we simplified the expression ![]() and got a new simplified expression
and got a new simplified expression ![]() . The value of the new simplified expression is still 0.5
. The value of the new simplified expression is still 0.5
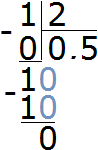
Thus, no matter how we simplify an expression, the value of the resulting expressions is still 0.5. So the simplification was performed correctly at each step. This is what we should strive for when simplifying expressions - the value of the expression should not be affected by our actions.
It is often necessary to simplify variable expressions. The same simplification rules apply to them as to numeric expressions. Any permissible actions can be performed as long as the value of the expression does not change.
Let's look at a few examples.
Example 1. Simplify the expression 5.21s × t × 2.5
To simplify this expression, you can multiply the numbers separately and multiply the variables separately. This task is very similar to the one we looked at when we were learning how to determine the coefficient:
5.21s × t × 2.5 = 5.21 × 2.5 × s × t = 13.025 × st = 13.025st
Thus, the expression 5.21s × t × 2.5 is simplified to 13.025st.
Example 2. Simplify the expression -0.4 × (-6.3b) × 2
The second product (-6,3b) can be translated into a form we can understand, namely, to write in the form (-6,3)×b, then multiply the numbers separately and multiply the variables separately:
−0.4 × (−6.3b) × 2 = −0.4 × (−6.3) × b × 2 = 5.04b
Thus, the expression -0.4 × (-6.3b) × 2 is simplified to 5.04b
Example 3. Simplify the expression 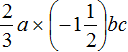
Let's break down this expression in more detail to see clearly where the numbers are and where the variables are:
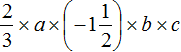
Now multiply the numbers separately and multiply the variables separately:

Thus, the expression 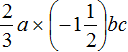 is simplified to -abc. This solution can be written in shorter form:
is simplified to -abc. This solution can be written in shorter form:
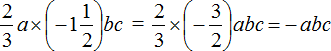
When simplifying expressions, fractions can be reduced in the process of solving them, not at the very end as we did with regular fractions.
For example, if we come across an expression like ![]() while solving it, it is not necessary to calculate the numerator and denominator and do something like this:
while solving it, it is not necessary to calculate the numerator and denominator and do something like this:
![]()
Fractions can be reduced by choosing a factor in the numerator and a factor in the denominator and reducing those factors by their greatest common divisor. In other words, use a short version of fraction reduction in which we do not describe in detail what the numerator and denominator were divided by.
For example, in the numerator a multiplier of 12 and in the denominator a multiplier of 4 can be reduced by 4. We keep the four in mind, and after dividing 12 and 4 by this four, we write the answers next to these numbers, crossing them out beforehand
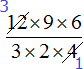
Then in the numerator the factor 9 and in the denominator the factor 3 can be reduced by 3
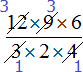
Then in the numerator the factor 6 and in the denominator the factor 2 can be reduced by 2

Now you can multiply the resulting small multipliers. In this case they are few and can be multiplied in mind:
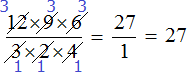
Over time you may find that by solving this or that problem, expressions begin to "get shorter", so it is desirable to get used to quick calculations. What you can calculate in your head, you should calculate in your head. What can be reduced quickly must be reduced quickly.
Example 4. Simplify the expression ![]()
Let's multiply the numbers separately and the variables separately:
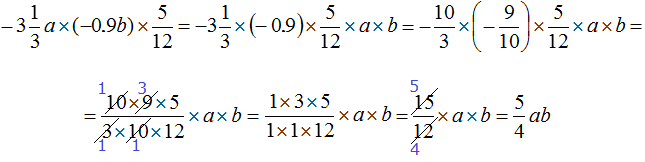
Thus, the expression ![]() is simplified to
is simplified to ![]()
Example 5. Simplify the expression 
Let's multiply the numbers separately and the variables separately:
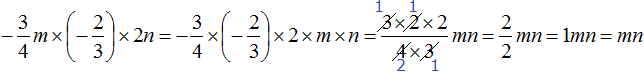
Thus, the expression  is simplified to mn.
is simplified to mn.
Example 6. Simplify the expression 
Let's write down this expression in more detail in order to see clearly where the numbers are and where the variables are:
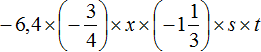
Now multiply the numbers separately and the variables separately. For convenience, the decimal -6.4 and the mixed number ![]() can be converted into fractions:
can be converted into fractions:

Thus, the expression  is simplified to -6.4stx
is simplified to -6.4stx
The solution for this example can be written in a much shorter form. It would look as follows:

Example 7. Simplify the expression ![]()
Multiply numbers andvariables separately. For convenience, the mixed number ![]() and decimals 0.1 and 0.6 can be converted into fractions:
and decimals 0.1 and 0.6 can be converted into fractions:
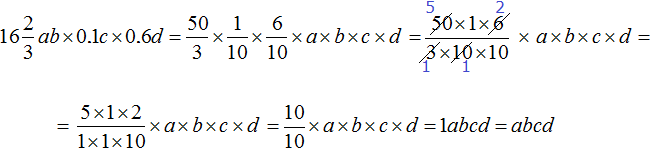
Thus, expression ![]() is simplified to abcd. If we skip the details, this solution can be written much shorter:
is simplified to abcd. If we skip the details, this solution can be written much shorter:
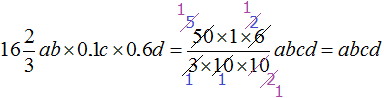
Note how the fraction is reduced. New multipliers that result from the reduction of previous multipliers are also allowed to be reduced.
Now let's talk about what we should not do. When simplifying expressions, you absolutely cannot multiply numbers andvariables if the expression is a sum and not a product.
For example, if you want to simplify the expression 5a + 4b, you cannot write as follows:

This is equivalent to if we were asked to add two numbers and we multiplied them instead of adding them.
By substituting any values of the variables a and b, the expression 5a +4b turns into an ordinary numeric expression. Suppose that the variables a and b have the following values:
a = 2, b = 3
Then the value of the expression will be 22
5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22
First the multiplication is performed, and then the results are added up. And if we tried to simplify this expression by multiplying the numbers and variables, we would get the following:
5a + 4b = 5 × 4 × a × b = 20ab
20ab = 20 × 2 × 3 = 120
It turns out a completely different value of the expression. In the first case it is 22, in the second case it is 120. This means that the simplification of the expression 5a + 4b was done incorrectly.
After simplifying an expression, its value should not change with the same values of the variables. If substituting any values of the variables into the original expression yields one value, then after simplifying the expression, the value should be the same as before the simplification.
You can't really do anything with the expression 5a + 4b. It is not simplified.
If an expression contains like terms, they can be added if our goal is to simplify the expression.
Example 8. Simplify the expression 0.3a-0.4a+a
To simplify this expression, you can combine like terms:
0.3a − 0.4a + a = 0.3a + (−0.4a) + a = (0.3 + (−0.4) + 1)×a = 0.9a
or shorter: 0,3a − 0.4a + a = 0.9a
Thus, the expression 0.3a-0.4a+a is simplified to 0.9a
Example 9. Simplify the expression −7.5a − 2.5b + 4a
To simplify this expression, you can combine like terms:
−7.5a − 2.5b + 4a = −7.5a + (−2.5b) + 4a = ((−7.5) + 4)×a + (−2.5b) = −3.5a + (−2.5b)
or shorter: −7.5a − 2.5b + 4a = −3.5a + (−2.5b)
The summand (-2.5b) remained unchanged because there was nothing to add to it.
Example 10. Simplify the expression ![]()
To simplify this expression, you can combine like terms:
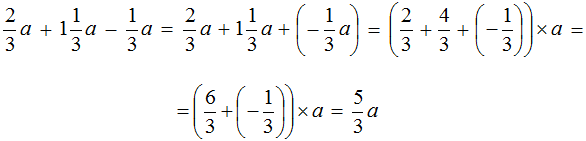
The coefficient of ![]() was converted to an improper fraction for ease of calculation.
was converted to an improper fraction for ease of calculation.
Thus, the expression ![]() is simplified to
is simplified to ![]()
Example 11. Simplify the expression ![]()
To simplify this expression, you can combine like terms:
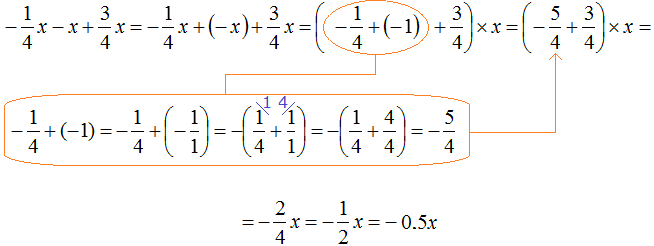
Thus, the expression ![]() is simplified to
is simplified to ![]() .
.
In this example, it would be more reasonable to add the first and last coefficients first. In this case we would get a short solution. It would look like this:
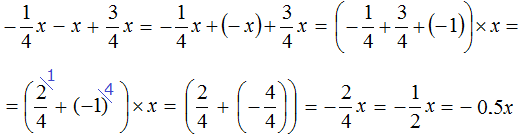
Example 12. Simplify the expression ![]()
To simplify this expression, you can combine like terms:

Thus, the expression ![]() is simplified to
is simplified to 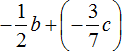 .
.
The summand 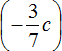 remained unchanged because there was nothing to add to it.
remained unchanged because there was nothing to add to it.
This solution can be written in a much shorter form. It would look as follows:
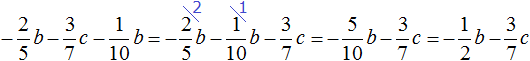
The short solution omits the steps of replacing subtraction with addition and a detailed record of how fractions were reduced to a common denominator.
Another difference is that in the detailed solution the answer looks like 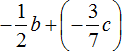 , and in the short solution it looks like
, and in the short solution it looks like ![]() . In fact, it is the same expression. The difference is that in the first case, the subtraction has been replaced by the addition, because in the beginning, when we wrote down the solution in the detailed form, we replaced the subtraction with the addition wherever possible, and this replacement is retained for the answer.
. In fact, it is the same expression. The difference is that in the first case, the subtraction has been replaced by the addition, because in the beginning, when we wrote down the solution in the detailed form, we replaced the subtraction with the addition wherever possible, and this replacement is retained for the answer.
Identity. Equivalent Expressions
After we simplify an expression, it becomes simpler and shorter. To check if an expression is simplified correctly, just substitute any values of the variables first into the previous expression to be simplified and then into the new expression that has been simplified. If the value in both expressions is the same, it means that the expression is simplified correctly.
Consider a simple example. Let the expression 2a × 7b be simplified. To simplify this expression, we can multiply the numbers and variables separately:
2a × 7b = 2 × 7 × a × b = 14ab
Let's check if we have simplified the expression correctly. To do this, substitute any values of variables a and b first into the first expression that we wanted to simplify, and then into the second expression that we simplified.
Let the values of variables a, b be as follows:
a = 4
b = 5
Substitute them into the first expression 2a × 7b
2a × 7b = 2 × 4 × 7 × 5 = 280
Now substitute the same values of the variables in the expression that results from simplifying the expression 2a × 7b, namely, in the expression 14ab
14ab = 14 × 4 × 5 = 280
We see that when a = 4 and b = 5, the value of the first expression 2a × 7b and the value of the second expression 14ab are equal
2a × 7b = 2 × 4 × 7 × 5 = 280
14ab = 14 × 4 × 5 = 280
The same will happen for any other values. For example, let a = 1 and b = 2
2a × 7b = 2 × 1 × 7 × 2 = 28
14ab = 14 × 1 × 2 = 28
Thus, the expressions 2a × 7b and 14ab are equal to the same value for all values of the variables. Such expressions are called equivalent expressions.
We conclude that between the expressions 2a × 7b and 14ab we can put an equal sign, because they are equal to the same value:
2a × 7b = 14ab
An equality is any expression that is joined by an equal sign (=).
An equality of the form 2a × 7b = 14ab is called an identity equasion.
An identity is an equality that is true for all values of the variables.
Other examples of identities:
a + b = b + a
a(b + c) = ab + ac
a(bc) = (ab)c
Yes, the laws of mathematics we studied are identities.
True numerical equations are also identities. For example:
2 + 2 = 4
3 + 3 = 5 + 1
10 = 7 + 2 + 1
When solving a complex problem, in order to simplify the calculation, a complex expression is replaced by a simpler expression that is identically equal to the previous one.
For example, we simplified the expression 2a × 7b, and obtained a simpler expression 14ab. This simplification can be called an identity transformation.
You will often see an assignment that says "prove equality of an equation", followed by the equality you want to prove. Usually this equality consists of two parts: the left and the right parts of the equality. Our task is to perform identity transformations with one part of the equality and get the other part. Or perform identity transformations on both parts of the equality and make both parts of the equality have the same expressions.
For example, prove that the equality 0.5a × 5b = 2.5ab is an identity.
Simplify the left part of this equality. To do this, multiply the numbers and variables separately:
0.5 × 5 × a × b = 2.5ab
2.5ab = 2.5ab
As a result of a small identity transformation, the left part of the equality became equal to the right part of the equality. So we proved that the equality 0.5a × 5b = 2.5ab is an identity.
From identity transformations we have learned to add, subtract, multiply and divide numbers, reduce fractions, add like terms, and simplify some expressions.
But these are not all of the identity transformations that exist in mathematics. There are many more identical transformations. We will see more than once in the future.
Exercises:


- multiply a by three, and from that product subtract fifteen
- multiply t by nine, and add thirty-five to the product.
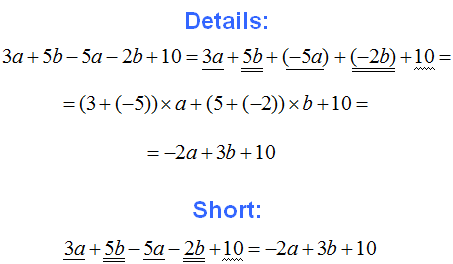

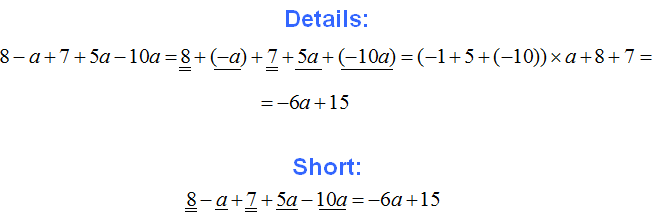

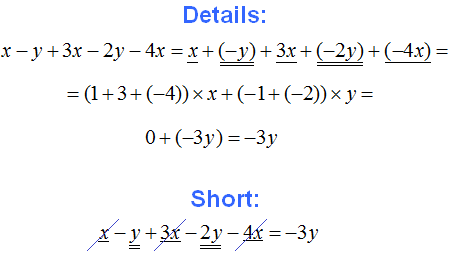
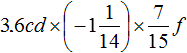
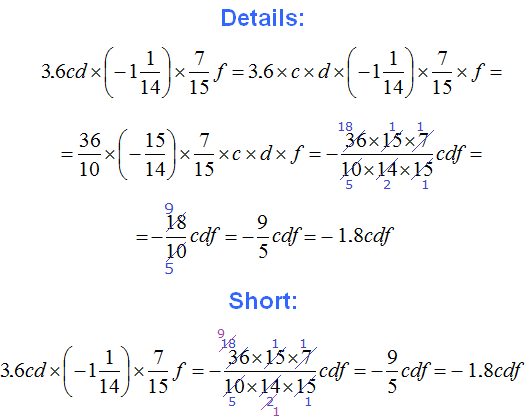
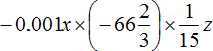

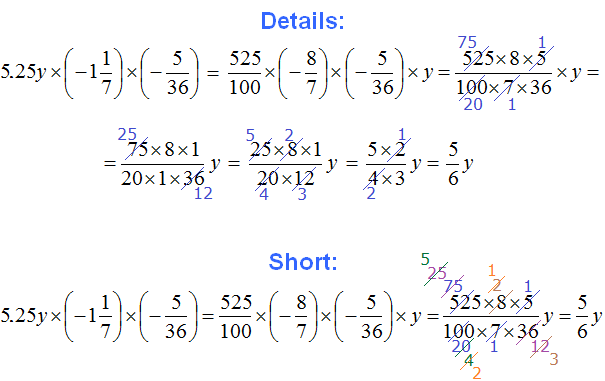
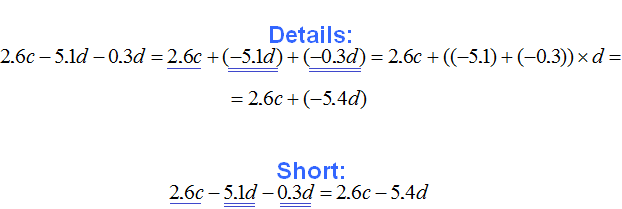
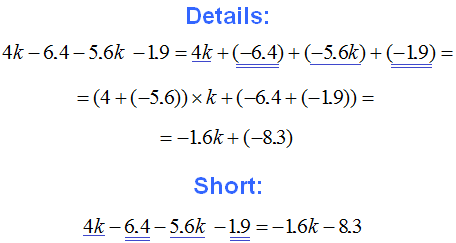

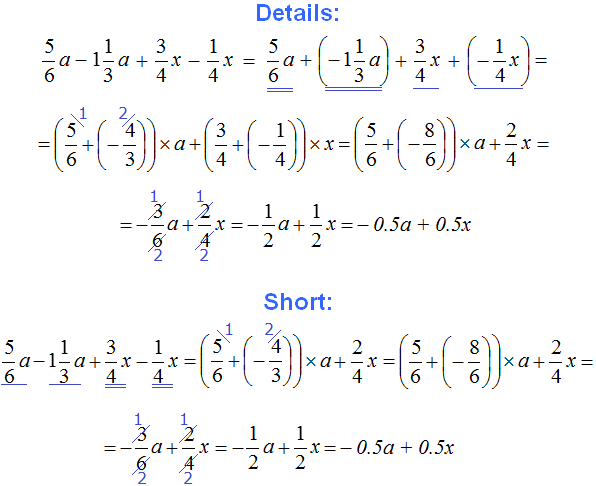
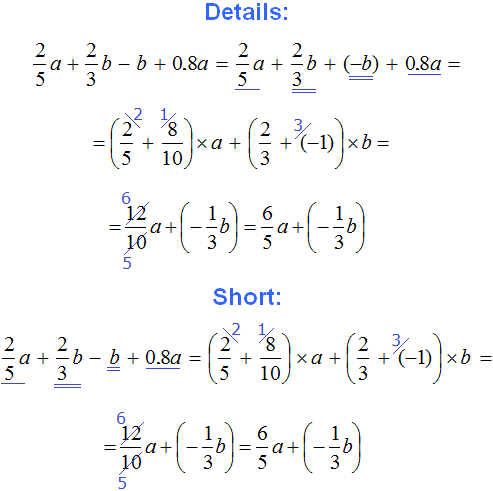
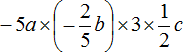
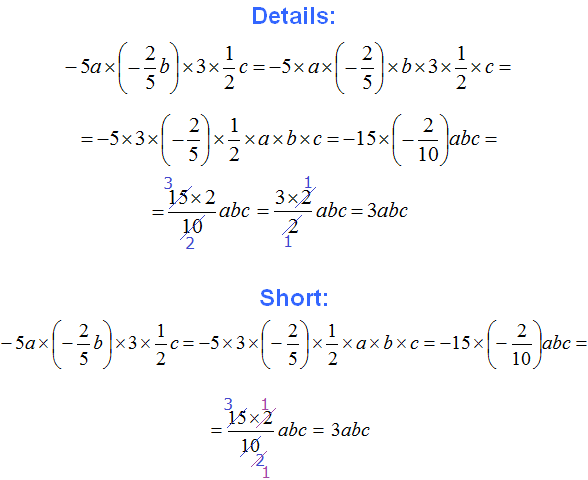
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.