Solving a task usually consists of finding the value of some quantity by logical reasoning and calculations. For example, find the speed, time, distance, mass of an object, or amount of something.
Such a task can be solved by using an equation. To do this, the desired value is denoted by a variable, then by logical reasoning the equation is composed and solved. After solving the equation, you check to see if the solution to the equation satisfies the conditions of the task.
Writing expressions containing the unknown
The solution of the task is accompanied by the composition of the equation to this task. At the initial stage of studying tasks it is desirable to learn to make up letter expressions describing this or that situation in life. This stage is not complicated and can be studied in the process of solving the task itself.
Consider a few situations that can be written down using a mathematical expression.
Task 1. The father is x years old. Mom is two years younger. The son is three times younger than the father. Write the age of each using expressions.
Solution:
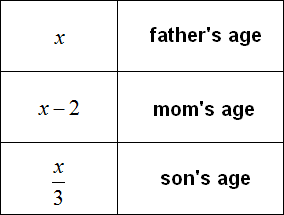
Task 2. Father is x years old, mother is 2 years younger than father. Son is 3 times younger than father, daughter is 3 times younger than mother. Write the age of each using expressions.
Solution:
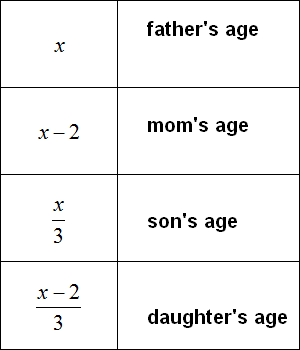
Task 3. Father is x years old, mother is 3 years younger than father. The son is 3 times younger than the father, the daughter is 3 times younger than the mother. How old are each of them if the total age of the father, mother, son, and daughter is 92?
Solution:
In this task, in addition to writing down the expressions, we need to calculate the age of each family member.
First, write down the age of each family member using expressions. We will take the age of the father as the variable x, and then use that variable to make the rest of the expressions:
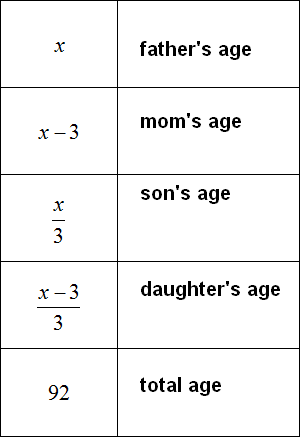
Now let's determine the age of each family member. To do this, we need to make and solve an equation. We have all the components of the equation ready. The only thing left to do is to put them together.
The total age of 92 was obtained by adding the ages of the father, mother, son and daughter:
father + mother + son + daughter = 92
For each age, we made up a mathematical expression. These expressions will be the components of our equation. Let's assemble our equation according to this diagram and the table above. That is, replace the words father, mother, son, daughter with their corresponding expression in the table:
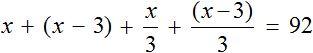
The expression corresponding to mom's age x - 3 was put in brackets for clarity.
Now let's solve the resulting equation. To begin with, you can open the brackets where you can:
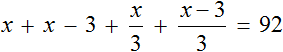
To free the equation from fractions, multiply both parts by 3
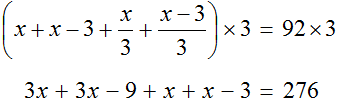
Solve the resulting equation using the known identity transformations:
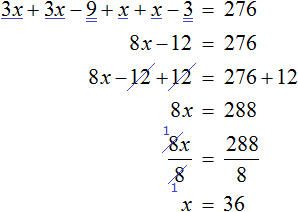
We found the value of variable x. This variable was responsible for the age of the father. So the age of the father is 36 years old.
Knowing the age of the father, we can calculate the ages of the other family members. To do this, substitute the value of variable x in those expressions that correspond to the age of a particular family member.
The task said that my mother is 3 years younger than my father. We denoted her age by the expression x - 3. The value of the variable x is now known, and to calculate mom's age, substitute the found value 36 instead of x in the expression x - 3
x - 3 = 36 - 3 = 33 years old mom.
The age of the other family members is determined similarly:
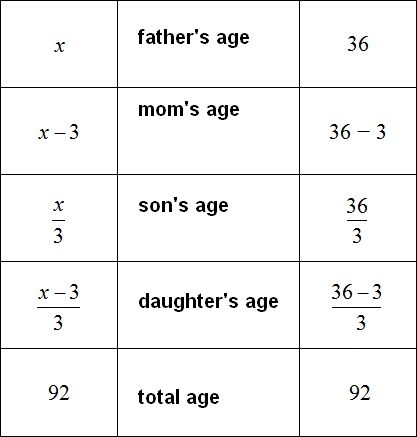
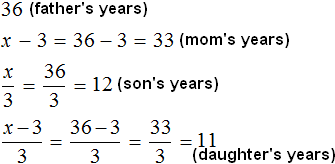
Checking:
![]()
Task 4. A kilogram of caviar costs x dollars. Write an expression that calculates how many kilograms of caviar you can buy for $300.
Solution:
If a kilogram of caviar costs x dollars, then you can buy ![]() kilograms of caviar for $300.
kilograms of caviar for $300.
Example. A kilogram of caviar costs 50 dollars. Then for 300 dollars you can buy ![]() , that is 6 kilograms of caviar.
, that is 6 kilograms of caviar.
Task 5. x dollars was used to buy 5 kilograms of strawberries. Write an expression that calculates how many dollars one kilogram of strawberries costs.
Solution:
If x dollars was paid for 5 kg of strawberries, then one kilogram will cost ![]() dollars
dollars
Example. Five kilos of strawberries were bought for $300. Then one kilogram of strawberries will cost ![]() , i.e. $60.
, i.e. $60.
Task 6. Tom, John, and Leo went to the cafeteria during recess and bought a large pizza and a glass of fresh juice. The large pizza cost x dollars and the coffee cost $15. Determine the cost of the pizza if you know that $120 was paid for everything?
Solution:
Of course, this task is simple and can be solved without resorting to an equation. To do this, subtract the cost of three glasses of juice from $120 (15 × 3), and divide the result by 3
![]()
But our goal is to make an equation to the task and solve this equation. So, the cost of a large pizza is x dollars. Only three of them were bought. So if we increase the cost by three times, we get an expression describing how many dollars were paid for the three large pizzas.
3x — the cost of three large pizzas
And the cost of three glasses of juice can be written as 15 × 3. 15 is the cost of one glass of juice, and 3 is the multiplier (Tom, John, and Leo) that triples that cost.
Under the terms of the task, $120 is paid for everything. We already have an approximate scheme of what needs to be done:
Cost of three large pizzas + cost of three glasses of fresh juice = $120
The expressions describing the cost of three pizzas and three glasses of juice are ready. These are expressions 3x and 15 × 3. Use the scheme to make an equation and solve it:
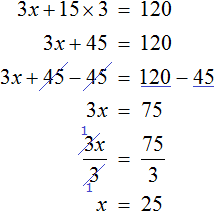
So, the cost of one large pizza is $25.
The task is solved correctly only if the equation to it is written correctly. Unlike ordinary equations by which we learn to find the roots, problem-solving equations have their own specific application. Each component of such an equation can be described in verbal form. When making an equation, it is imperative that we understand why we are including one component or another and why it is needed.
You must also remember that after solving the equation, the left-hand side will have to equal the right-hand side. The equation composed must not contradict this idea.
Let's imagine that the equation is a scale with two bowls and a screen showing the state of the scale.
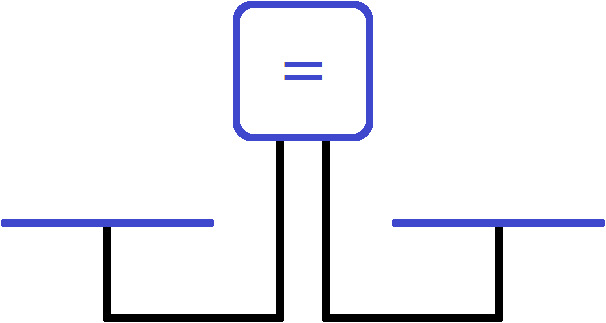
At this point, the screen shows an equal sign. It is clear why the left bowl is equal to the right bowl - there is nothing on the scales. The state of the scales and the absence of anything on the bowls will be recorded with the following equality:
0 = 0
Put a watermelon on the left side of the scale:
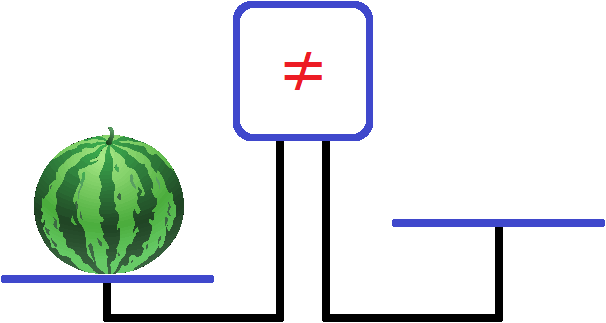
The left bowl outweighed the right bowl and the screen sounded an alarm, showing a not equal sign ( ≠ ). This sign indicates that the left bowl is not equal to the right bowl.
Now let's try to solve the problem. Let's find out how much the watermelon on the left bowl weighs. But how can we find this out? Our scales are only for checking if the left bowl is equal to the right one.
Equations come to the rescue. Recall that an equation contains a variable whose value must be found. The scale in this case is the equation itself, and the mass of the watermelon is the variable, the value of which needs to be found. Our goal is to get this equation right. That is, to align the scales so that we can calculate the mass of the watermelon.
To level the scales, we can put some heavy object on the right-hand bowl. For example, let's put a weight of 7 kilograms there.
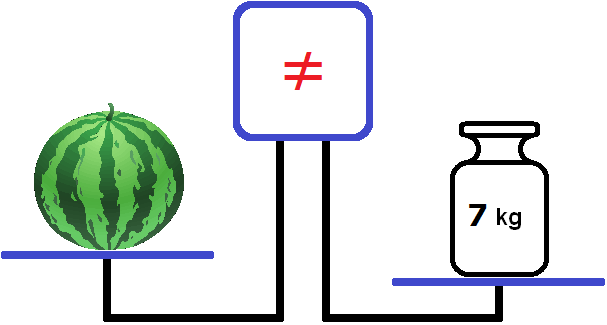
Now the right bowl outweighs the left bowl. The screen still shows that the bowls are not equal.
Let's try to put a weight of 4 kg on the left bowl
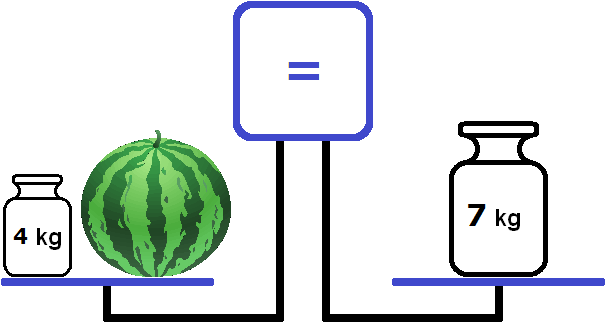
Now the scales are aligned. In the picture you can see that the left bowl is at the level of the right bowl. And the screen shows an equal sign. This sign says that the left bowl is equal to the right bowl.
So we got an equation - an equality that contains the unknown. The left bowl is the left side of the equation, consisting of the components 4 and the variable x (watermelon mass), and the right bowl is the right side of the equation, consisting of the component 7.
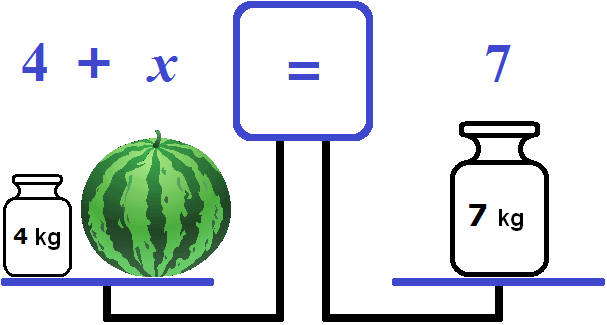
Well, it's not hard to guess that the root of the equation 4 + x = 7 is 3. So the mass of the watermelon is 3 kg.
The same is true for the other tasks. To find some unknown value, various elements are added to the left or right side of the equation: terms, multipliers, expressions. In school tasks, these elements may already be given. All that remains is to structure them correctly and construct the equation. In this example, we were trying weights of different weights to calculate the mass of the watermelon.
Naturally, the data given in the task must first be reduced to a form in which they can be included in the equation.
Consider the following task. The father's age is equal to the age of the son and daughter together. The son is twice as old as the daughter and twenty years younger than the father. How old are each?
The daughter's age can be denoted by x. If the son is twice as old as the daughter, his age will be denoted by 2x. The condition of the problem says that together the age of the daughter and the son are equal to the age of the father. So the father's age will be denoted by the sum x + 2x

In the expression x + 2x you can give like terms. Then the age of the father will be denoted as 3x
Now let's make an equation. We need to get an equation where we can find the unknown x. Let's use weights. On the left hand side put the age of the father (3x), and on the right hand side put the age of the son (2x)
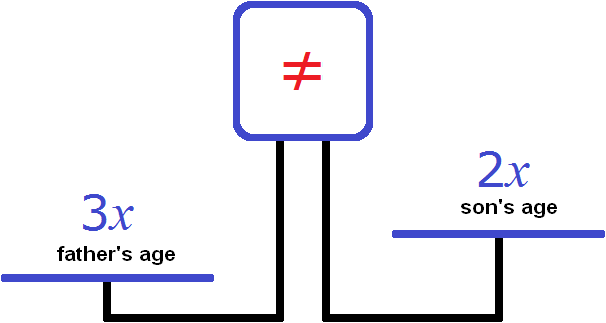
It is clear why the left bowl outweighs the right and why the screen shows the sign ( ≠ ). After all, it is logical that the age of the father is greater than the age of the son.
But we need to equalize the scales to be able to calculate the unknown x. To do this we need to add some number to the right-hand scale. What exact number is given in the task. The condition said that the son is 20 years younger than his father. So 20 years is the number to put on the scale.
The scales will even out if we add these 20 years to the right side of the scale. In other words, raise the son to the age of the father.
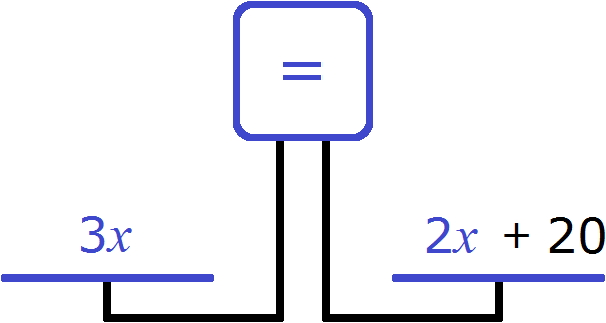
Now the scales are aligned. We got the equation 3x = 2x + 20, which is easy to solve:
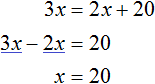
At the beginning of this task, we used the variable x to represent our daughter's age. Now we found the value of this variable. The daughter is 20 years old.
Next, it was said that the son is two years older than the daughter, so the son is (20 × 2), that is, 40 years old.
Finally, let's calculate the age of the father. It was said in the problem that he is equal to the sum of the ages of the son and daughter, that is, (20 + 40) years old.

Let's return to the middle of the task and note one point. When we put the age of the father and the age of the son on the scale, the left cup outweighed the right

But we solved this problem by adding another 20 years to the right-hand scale. As a result, the scales aligned and we got the equality 3x = 2x + 20

But we could not add those 20 years to the right cup, but subtract them from the left. We would have obtained equality and in that case
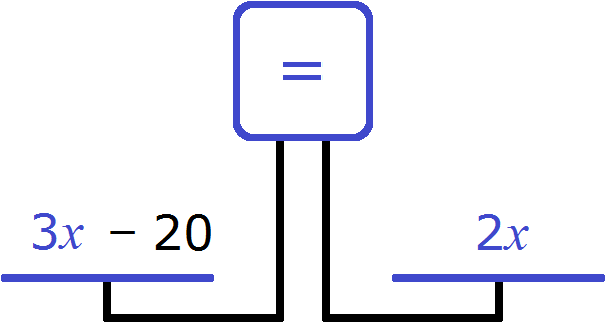
This time you get the equation 3x -20 = 2x. The root of the equation is still 20
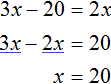
That is, the equations 3x = 2x + 20 and 3x -20 = 2x are equipotent. And we remember that equal equations have the same roots. If you look closely at these two equations, you can see that the second equation is obtained by moving the number 20 from the right side to the left side with the opposite sign. And this action, as stated in the previous lesson, does not change the roots of the equation.
Also note that at the beginning of the task, the ages of each family member could be given by other expressions.
Say the age of the son is x, and since he is two times older than the daughter, the age of the daughter is ![]() (make her half as old as her son). And the age of the father, since it is the sum of the ages of the son and daughter, denote by the expression
(make her half as old as her son). And the age of the father, since it is the sum of the ages of the son and daughter, denote by the expression ![]() . And finally, to build a logically correct equation, add 20 to the age of the son, because the father is twenty years older. The result is a very different equation
. And finally, to build a logically correct equation, add 20 to the age of the son, because the father is twenty years older. The result is a very different equation
![]() .
.
Let's solve this equation
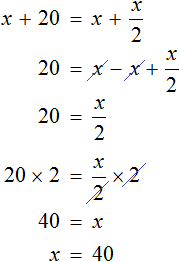
As you can see, the answers to the task have not changed. The son is still 40 years old. The daughter is still ![]() years old, and the father is 40 + 20 years old.
years old, and the father is 40 + 20 years old.
In other words, the task can be solved by different methods. So you should not be discouraged if you cannot solve a particular problem. But you should keep in mind that there are the easiest ways to solve the problem. It is possible to get to the city center by different routes, but there is always the most convenient, fastest and safest route.
Examples of problem solving
Task 1. There are a total of 30 notebooks in two packs. If two notebooks were moved from the first stack to the second stack, the first stack would contain twice as many notebooks as the second stack. How many notebooks were in each pack?
Solution:
Denote by x the number of notebooks that were in the first stack. If the total number of notebooks was 30, and the variable x is the number of notebooks in the first stack, then the number of notebooks in the second stack will be denoted by the expression 30 - x. That is, from the total number of notebooks we subtract the number of notebooks in the first stack, and thus we obtain the number of notebooks in the second stack.

Further it is said that if you move two notebooks from the first pack to the second pack, there will be twice as many notebooks in the first pack. So let's remove two notebooks from the first stack
![]()
and add these two notebooks to the second pack
![]()
The expressions from which we will compose the equation now take the following form:

Let's try to make an equation out of the available expressions. Put both stacks of notebooks on the scales
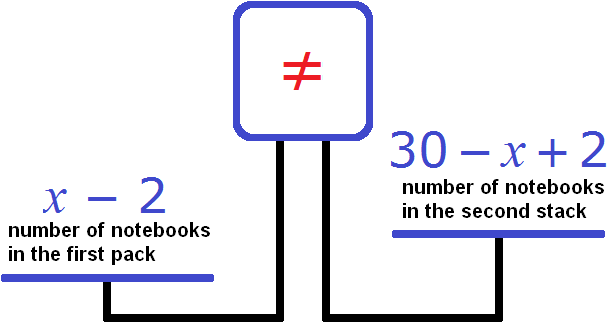
The left bowl is heavier than the right one. This is because the problem statement says that after taking two notebooks from the first stack and putting them into the second stack, the number of notebooks in the first stack became twice as many as in the second stack.
To equalize the scales and get the equation, let's double the right-hand side. To do this, multiply it by 2
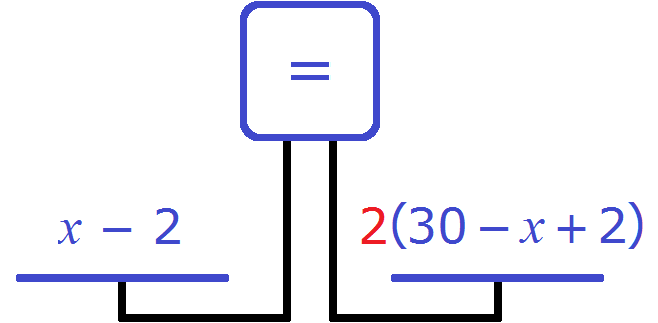
We obtain the equation x-2 = 2(30 - x +2). Solve this equation:
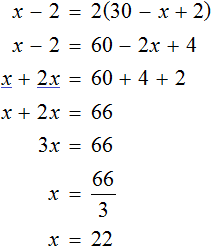
We denoted the first packet by the variable x. Now we have found its value. The variable x is 22. So there were 22 notebooks in the first stack.
And we denoted the second tutu by the expression 30 - x, and since the value of the variable x is now known, we can calculate the number of notebooks in the second tutu. It is equal to 30 - 22, i.e. 8 pieces.
Task 2. Two people were peeling potatoes. One peeled two potatoes per minute and the other peeled three potatoes. Together they peeled 400 pieces. How long did each work, if the second worked 25 minutes longer than the first?
Solution:
Denote by x the time the first person worked. Since the second person worked 25 minutes longer than the first person, his time will be denoted by x + 25
The first worker peeled 2 potatoes per minute, and since he worked x minutes, he peeled a total of 2x potatoes.
The second person peeled three potatoes per minute, and since he worked x + 25 minutes, he peeled a total of 3(x + 25) potatoes.
Together they peeled 400 potatoes

From the available components let us make and solve the equation. The left side of the equation will be the potatoes peeled by each person, and the right side will be their sum:
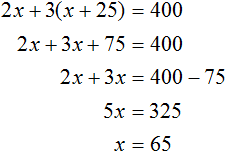
At the beginning of this task, we used the variable x to denote the working time of the first person. Now we found the value of this variable. The first person worked for 65 minutes.
And the second person worked x + 25 minutes, and since the value of the variable x is now known, we can calculate the working time of the second person - it is 65 + 25, that is, 90 minutes.
The task from the Russian algebra textbook. (Their currency is rubles and kopecks (like dollars and cents))
Of the varieties of tea is a mixture of 32 kg. A kilogram of the first grade costs 8 rubles, and the second grade 6 rubles. 50 kop. How many kilos of both varieties, if a kilo of mixture costs (no profit and loss) 7 rubles. 10 kop.
Solution:
Denote by x the mass of first grade tea. Then the mass of second grade tea will be denoted by the expression 32 - x
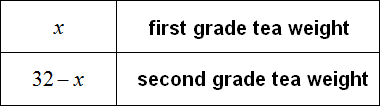
A kilogram of first grade tea costs 8 rubles. If you multiply these eight rubles by the number of kilograms of first grade tea, you can find out how many rubles it cost x kilograms of first grade tea.
A kg of second class tea costs 6 roubles. 50 kopecks. If the price is 6 rubles. 50 kopecks times 32 - x, we will find out how much it cost 32 - x kg of tea of the second sort.
The condition says that a kilogram of mixture costs 7 rubles. 10 kopecks. All in all 32 kg of the mixture were produced. Multiply 7 rubles. 10 kopecks by 32 we can find out how much 32 kg of the mixture costs.
The expressions from which we will make the equation now take the following form:

Let's try to make an equation out of the available expressions. Let's put the cost of mixtures of first and second grade teas on the left scale, and on the right scale let's put the cost of 32 kg of mixture, i.e. the total cost of the mixture, which includes both varieties of tea:
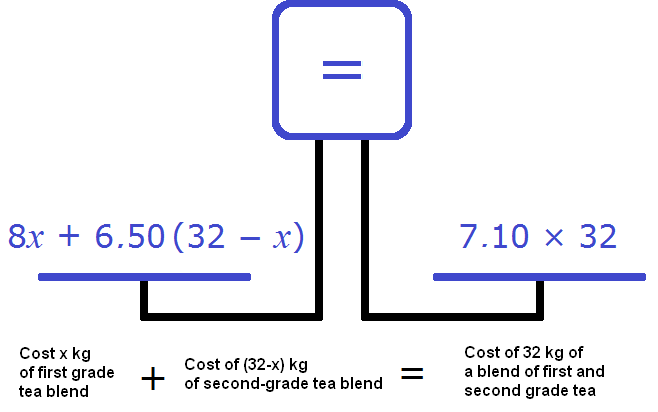
We get the equation 8x + 6.50(32 - x) = 7.10 * 32. Let's solve it:
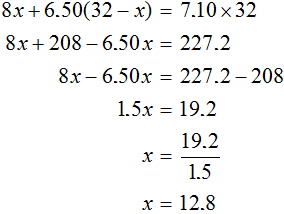
At the beginning of this task, we used the variable x to denote the mass of the first grade tea. Now we have found the value of this variable. The variable x is 12.8. This means that 12.8 kg of first grade tea was used to make the mixture.
We have used the expression 32 - x to represent the mass of second-grade tea, and since the value of the variable x is now known, we can calculate the mass of second-grade tea. It is 32 - 12.8, i.e. 19.2. This means that 19.2 kg of second grade tea were used to prepare the mixture.
Task 3. A cyclist rode some distance at a speed of 8 km/h. He had to return by another road, which was 3 km longer than the first road, and although he rode back at a speed of 9 km/h, he spent ![]() minutes more time. How long were the roads?
minutes more time. How long were the roads?
Solution:
Some tasks may involve topics that a person may not have studied. This task is one of those tasks. It touches on the concepts of distance, speed, and time. Accordingly, to solve such a problem, it is necessary to have an idea of the things mentioned in the problem. In our case, it is necessary to know what represents distance, speed and time.
In the task we need to find the distances of the two roads. We have to make an equation that will allow us to calculate these distances.
Let's remember how distance, speed, and time are interrelated. Each of these quantities can be described using a letter equation:
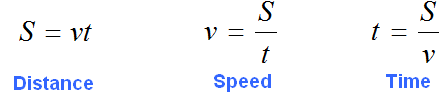
We will use the right side of one of these equations to make our own equation. To find out which one, go back to the text of the problem and pay attention to the following point:
...he spent ![]() minutes more time...
minutes more time...
Note the point where the cyclist spent ![]() minutes more on the way back. This clue tells us that we can use the equation
minutes more on the way back. This clue tells us that we can use the equation ![]() , namely its right-hand side. This will allow us to make an equation that contains the variable S.
, namely its right-hand side. This will allow us to make an equation that contains the variable S.
So we denote the length of the first road by S. The cyclist traveled this distance at a speed of 8 km/h. The time it took him to travel this distance is denoted by the expression ![]() , since time is the ratio of the distance traveled to the speed
, since time is the ratio of the distance traveled to the speed
The first distance traveled in ![]() hours
hours
The way back for the cyclist was longer by 3 km. Therefore its distance will be denoted by the expression S + 3. The cyclist rode this road at a speed of 9 km/h. Therefore, the time it took the cyclist to travel that distance is denoted by ![]() .
.
In ![]() the second distance is traveled
the second distance is traveled
Now let's make an equation out of the available expressions
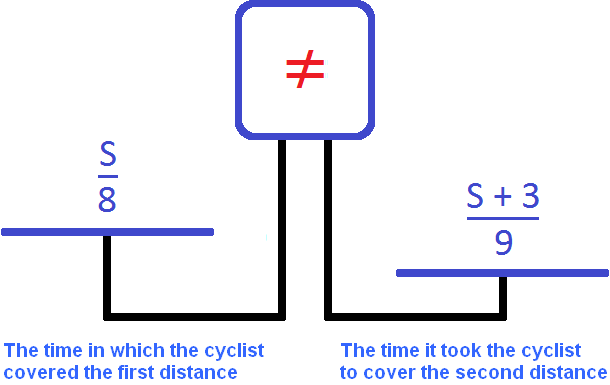
The right bowl is heavier than the left bowl. This is because the task says that the cyclist spent ![]() more time on the way back.
more time on the way back.
To balance the scales, we add these ![]() minutes to the left side. But first let's convert the minutes to hours, since the speed in the task is measured in kilometers per hour, not meters per minute.
minutes to the left side. But first let's convert the minutes to hours, since the speed in the task is measured in kilometers per hour, not meters per minute.
To convert ![]() minutes into hours, divide them by 60
minutes into hours, divide them by 60
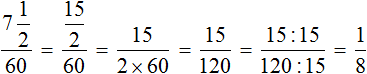
![]() minutes is
minutes is ![]() hours. Add these
hours. Add these ![]() hours to the left side of the equation:
hours to the left side of the equation:
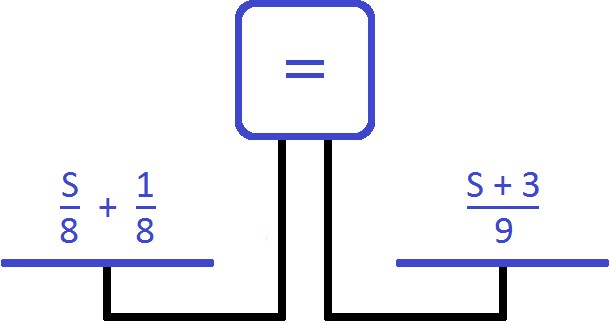
We obtain the equation ![]() . Let's solve this equation. To get rid of fractions, both parts can be multiplied by 72. Next, using the known identity transformations, find the value of the variable S
. Let's solve this equation. To get rid of fractions, both parts can be multiplied by 72. Next, using the known identity transformations, find the value of the variable S

Through the variable S we denoted the distance of the first road. Now we have found the value of this variable. The variable S is 15. So the distance of the first road is 15 km.
And the distance of the second road is S + 3. Since the value of the variable S is now known, we can calculate the distance of the second road. This distance is equal to the sum of 15 + 3, that is 18 km.
Task 4. Two cars walk along the highway at the same speed. If the first increases the speed by 10 km/h, and the second decreases the speed by 10 km/h, then the first car will pass the same distance in 2 h as the second car did in 3 h. At what speed are the cars traveling?
Solution:
Denote by v the speed of each car. Further in the problem there are hints: increase the speed of the first car by 10 km/h, and decrease the speed of the second car by 10 km/h. Let us use this hint
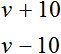
Further it is said that at such speeds (increased and decreased by 10 km/h) the first car will cover the same distance in 2 hours as the second car did in 3 hours. The phrase "as much" can be understood as "the distance traveled by the first car will be equal to the distance traveled by the second car".
The distance, as we remember, is determined by the formula S = vt. We are interested in the right part of this letter equation - it will allow us to make an equation containing the variable v.
So, at speed v + 10 km/h, the first car will travel 2(v+10) km and the second car will travel 3(v - 10) km. Under this condition, the cars will travel the same distance, so it is sufficient to connect the two expressions with an equal sign to obtain the equation. Then we obtain the equation 2(v+10) = 3(v - 10). Solve it:
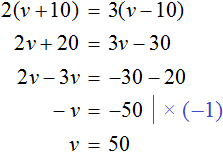
In the task condition it was said that the cars go at the same speed. We denoted this speed by the variable v. Now we have found the value of this variable. The variable v is 50. So the speed of both cars was 50 km/h.
Task 5. In 9 hours along the river the ship travels the same distance as in 11 hours against the stream. Find the boat's own speed if the speed of the river flow is 2 km/h.
Solution:
Denote by v the boat's own speed. The speed of the river flow is 2 km/h. The speed of the ship along the river will be v + 2 km/h, and against the current - (v - 2) km/h.
The statement of the task says that the boat takes the same distance in 9 hours upstream as it took 11 hours upstream. The phrase "the same distance" can be understood as "the distance traveled by the ship upstream in 9 hours is equal to the distance traveled by the ship against the river in 11 hours". That is, the distances will be the same.
The distance is determined by the formula S = vt. Let's use the right part of this letter equation to make our own equation.
So, the boat will travel 9(v + 2) km in 9 hours upstream, and 11(v - 2) km in 11 hours upstream. Since both expressions describe the same distance, let's equate the first expression to the second one. The resulting equation is 9(v + 2) = 11(v - 2)
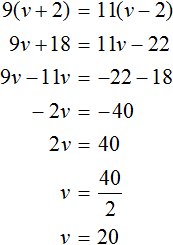
So the proper speed of the motorboat is 20 km/h.
When solving tasks, it is a useful habit to determine in advance on which set the solution is sought.
Suppose that in the task we needed to find the time in which the pedestrian travels the specified path. We denoted the time by the variable t, then made an equation containing this variable and found its value.
We know from practice that the time of motion of an object can take both integer and fractional values, for example 2 h, 1.5 h, and 0.5 h. Then we can say that the solution of this problem is searched for on the set of rational numbers Q, because each value of 2 h, 1.5 h, 0.5 h can be represented as a fraction.
So after you denote an unknown quantity by a variable, it is useful to specify which set this quantity belongs to. In our example, time t belongs to the set of rational numbers Q
t ∈ Q
You can also introduce a restriction for the variable t, stating that it can only take positive values. Indeed, if an object has spent a certain amount of time on the path, then this time cannot be negative. Therefore next to the expression t ∈ Q we specify that its value must be greater than zero:
t ∈ R, t > 0
If by solving the equation we get a negative value for the variable t, then we can conclude that the problem is solved incorrectly, because this solution will not satisfy the condition t ∈ Q, t > 0.
Another example. If we were solving a task that required us to find the number of people to do a particular job, we would denote this number by the variable x. In such a task the solution would be searched for on the set of natural numbers
x ∈ N
Indeed, the number of people is a whole number, e.g., 2 people, 3 people, 5 people. But not 1.5 (one whole person and half a person) or 2.3 (two whole persons and three tenths of a person).
Here we could specify that the number of people must be greater than zero, but the numbers included in the set of natural numbers N are themselves positive and greater than zero. In this set there are no negative numbers and no number 0. Therefore the expression x > 0 can be omitted.
Task 6. A team of 2.5 times as many painters as carpenters arrived to repair a school. Soon the foreman added four more painters to the brigade, and transferred two carpenters to another site. As a result, there were four times as many painters as carpenters in the brigade. How many painters and how many carpenters were in the brigade originally
Solution:
Denote by x the carpenters who arrived initially for repairs.
The number of carpenters is an integer greater than zero. Therefore let us specify that x belongs to the set of natural numbers
x ∈ N
There were 2.5 times more painters than carpenters. Therefore, the number of painters will be denoted as 2.5x.
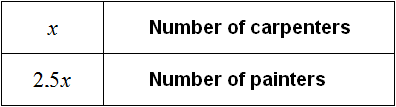
It goes on to say that the foreman included four more painters in the crew, and transferred two carpenters to another site. Let's do the same for our expressions. Reduce the number of carpenters by 2
![]()
And the number of painters will increase by 4
![]()
Now the number of carpenters and painters will be denoted by the following expressions:
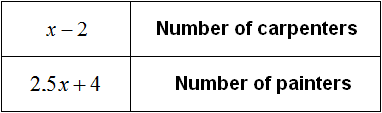
Let's try to make an equation out of the available expressions:
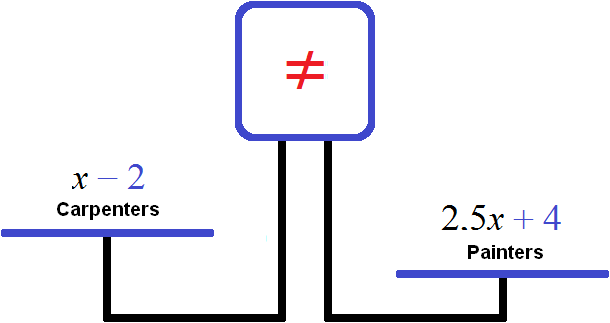
The right bowl is larger because after adding four more painters to the brigade and moving two carpenters to another site, the number of painters in the brigade is 4 times more than the number of carpenters. To equalize the scales, you need to quadruple the left bowl:
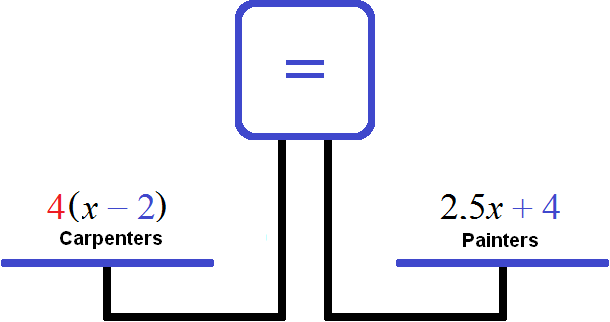
We got the equation ![]()
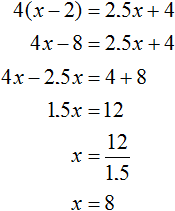
The variable x was used to represent the original number of carpenters. Now we have found the value of this variable. The variable x is equal to 8. So there were 8 carpenters in the team originally.
The number of painters was expressed as 2.5x, and since the value of the variable x is now known, we can calculate the number of painters, which is 2.5 × 8, that is, 20.
Go back to the beginning of the task and make sure that the condition x ∈ N is satisfied. The variable x is 8, and the elements of the set of natural numbers N are all numbers starting with 1, 2, 3 and so on to infinity. The same set includes the number 8, which we found.
8 ∈ N
The same can be said of the number of painters. The number 20 belongs to the set of natural numbers:
20 ∈ N
To understand the essence of the task and to correctly compose the equation, it is not necessary to use the model of scales with bowls. You can use other models: segments, tables, diagrams. You can come up with your own model, which would describe the essence of the task well.
Task 9. 30% of the milk was poured out of the can. This left 14 liters of milk in the can. How many liters of milk was in the can originally?
Solution:
We need to find the original number of liters in the can. Let's represent the number of liters as a line and sign this line as X

It is said that 30% of the milk was poured out of the beaker. Let's draw an approximate figure of 30%
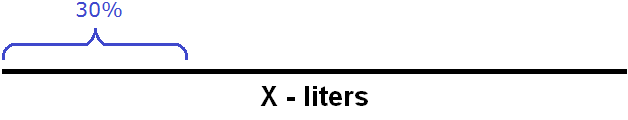
A percentage is, by definition, one hundredth of something. If 30% of the milk is poured, the other 70% is left in the can. This 70% is the 14 liters in the problem. Let's draw a picture of the remaining 70%
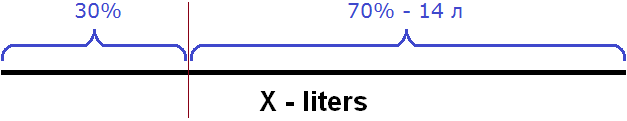
Now you can make an equation. Recall how to find the percentage of a number. To do this, the total amount of something is divided by 100 and the result is multiplied by the number of percentages you are looking for. Note that 14 liters, which is 70 percent, can be obtained in the same way: the original number of liters X divided by 100 and the result multiplied by 70. Equate all this to the number 14
![]()
Or get a simpler equation: write 70% as 0.70, then multiply by X and equate that expression to 14
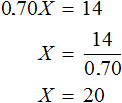
So originally there were 20 liters of milk in the can.
Task 9. Two alloys of gold and silver are taken. One has the quantity of these metals in the ratio of 1 : 9, and the other 2 : 3. How much of each alloy do you need to take to get 15 kg of a new alloy in which the gold and silver would be 1 : 4?
Solution:
Let's first try to find out how much gold and silver will be contained in 15 kg of the new alloy. The task says that the content of these metals should be 1 : 4, that is, one part of the alloy should contain gold, and four parts should contain silver. Then the total number of parts in the alloy will be 1 + 4 = 5, and the mass of one part will be 15 : 5 = 3 kg.
Let's determine how much gold is contained in 15 kg of the alloy. To do this, multiply 3 kg by the number of parts of gold:
3 kg × 1 = 3 kg
Let's determine how much silver will be contained in 15 kg of alloy:
3 kg × 4 = 12 kg
So an alloy with a mass of 15 kg will contain 3 kg of gold and 12 kg of silver. Now let's go back to the original alloys. We have to use each of them. Denote by x the mass of the first alloy, and the mass of the second alloy can be denoted by 15 - x

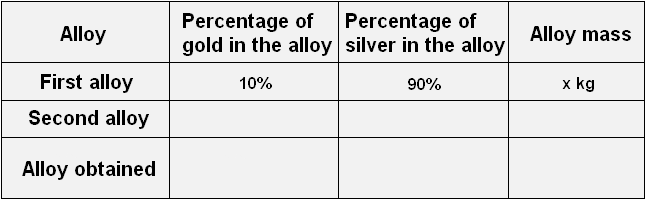
Express in percentages all the ratios given in the problem and fill in the following table with them:
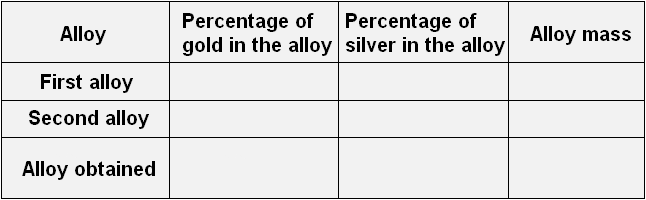
In the first alloy, gold and silver are in the ratio of 1 : 9. Then the total parts are 1 + 9 = 10. Of these, the gold is ![]() and the silver
and the silver ![]()
Let's transfer these data to the table. Let's enter 10% in the first line in the column "percentage of gold in the alloy", 90% in the first line in the column "percentage of silver in the alloy", and in the last column "mass of the alloy" we will enter the variable x, because that is how we designated the mass of the first alloy:
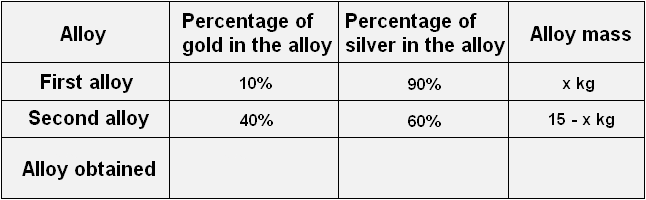
Do the same with the second alloy. Gold and silver in it are in the ratio of 2: 3. Then the total parts are 2 + 3 = 5. Of these, the gold is ![]() and the silver is
and the silver is ![]() .
.
Let's transfer these data to the table. Let's enter 40% in the second line in the column "percentage of gold in the alloy", 60% in the second line in the column "percentage of silver in the alloy", and in the last column "mass of the alloy" let's enter the expression 15 - x, because that is how we denoted the mass of the second alloy:
Let's fill in the last line. The resulting 15 kg alloy will contain 3 kg of gold, which is ![]() alloy, and silver will be
alloy, and silver will be ![]() alloy. In the last column write down the mass of the obtained alloy 15
alloy. In the last column write down the mass of the obtained alloy 15
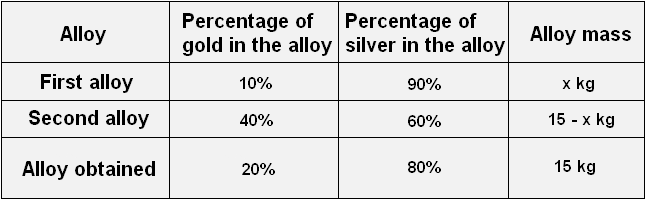
Now you can use this table to make equations. Recall the tasks of concentration, alloys, and mixtures. If we separately add up the gold of both alloys and equate this sum to the mass of gold of the resulting alloy, we can find out what the value of x equals.
Further, for convenience we will express percentages in decimals.
The first alloy had 0.10x gold and the second alloy had 0.40(15 - x) gold. Then the mass of gold in the resulting alloy will be the sum of the masses of gold of the first and second alloys and this mass is 20% of the new alloy. And 20% of the new alloy is 3 kg of gold, calculated earlier. The resulting equation is 0.10x + 0.40(15 - x) = 3. Let us solve this equation:
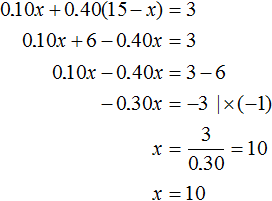
Initially we denoted by x the mass of the first alloy. Now we have found the value of this variable. The variable x is 10. And the mass of the second alloy we denoted by 15 - x, and since the value of the variable x is now known, we can calculate the mass of the second alloy, it is equal to 15 - 10 = 5 kg.
So in order to obtain a new alloy with a mass of 15 kg in which gold and silver would be 1 : 4, we would have to take 10 kg of the first alloy and 5 kg of the second alloy.
The equation could also be made using the second column of the resulting table. Then we would get the equation 0.90x + 0.60(15 - x) = 12. The root of this equation is also 10.
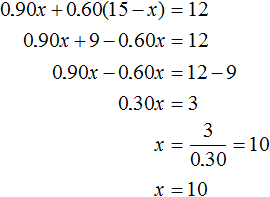
Task 10. There is an ore from two layers with copper grades of 6% and 11%. How much poor ore must be taken to get 20 tons with a copper content of 8% when mixed with the rich ore?
Solution:
Denote by x the mass of poor ore. Since 20 tons of ore are to be obtained, 20 - x will be taken from the rich ore. Since the copper content in the poor ore is 6%, x tons of ore will contain 0.06x tons of copper. The rich ore has a copper content of 11%, and 20 - x tons of rich ore will contain 0.11(20 - x) tons of copper.
The resulting 20 tons of ore should have a copper content of 8%. This means that 20 tons of ore will contain 20 × 0.08 = 1.6 tons of copper.
Add 0.06x and 0.11(20 - x) and equate the sum to 1.6. We obtain the equation 0.06x + 0.11(20 - x) = 1.6
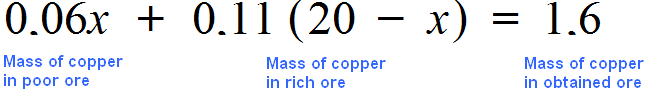
Let's solve this equation:
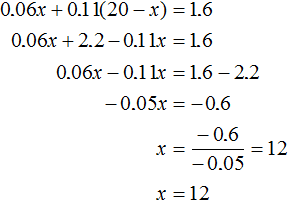
So, to get 20 tons of ore with 8% copper content, you need to take 12 tons of poor ore. The rich ore will be taken 20 - 12 = 8 tons.
Task 11. By increasing the average speed from 250 to 300 meters/minute, the athlete began to run the distance 1 minute faster. What is the length of the distance?
Solution:
The length of the course (or distance of the course) can be described by the following letter equation:
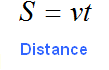
Let's use the right side of this equation to make our own equation. Initially, the athlete ran the distance at a speed of 250 meters per minute. At this speed, the length of the course would be described by the expression 250t
Then, the athlete increased her speed to 300 metres per minute. At this speed, the length of the course would be described by the expression 300t
Note that the length of the course is a constant. Whether the athlete increases her speed or decreases it, the length of the distance will remain the same.
This allows us to equate 250t with 300t, since both describe the same length.
250t = 300t
But the problem says that at a speed of 300 meters per minute, the athlete began to run the distance 1 minute faster. In other words, at 300 meters per minute, the running time will decrease by one. Therefore, in the equation 250t = 300t on the right hand side, the time should be reduced by one:
![]()
We get the simplest equation. Let's solve it:
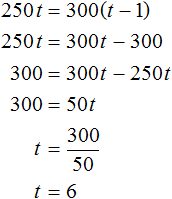
At a speed of 250 meters per minute, the athlete runs the distance in 6 minutes. Knowing the speed and time, you can determine the length of the course:
S = 250 × 6 = 1500 m
And at 300 meters per minute, the athlete runs the distance in t - 1, that is, in 5 minutes. As stated earlier, the length of the distance does not change:
S = 300 × 5 = 1500 m
Task 12. A rider catches up with a pedestrian 15 km ahead of him. In how many hours will the rider catch up with the pedestrian, if the first rides 10 km every hour and the second rides only 4 km?
Solution:
This task is a motion task. It can be solved by determining the speed of approach and dividing the initial distance between the rider and the pedestrian by that speed.
The speed of convergence is determined by subtracting the slower speed from the faster speed:
10 km/h - 4 km/h = 6 km/h (approach speed)
With each hour, the distance of 15 kilometers will decrease by 6 kilometers. To find out when it is completely shortened (when the rider catches up with the pedestrian), divide 15 by 6
15 : 6 = 2,5 h
2.5 hours is two whole hours and a half hour. And half an hour is 30 minutes. So the rider will catch up with the pedestrian in two hours and 30 minutes.
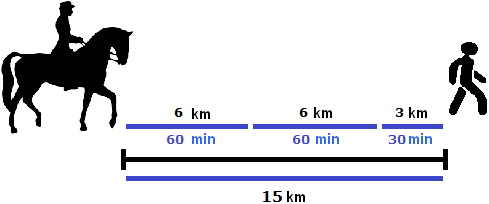
Let's solve this problem using an equation.
Assume that the pedestrian and the rider set out from the same place. The pedestrian left before the rider and managed to cover 15 km
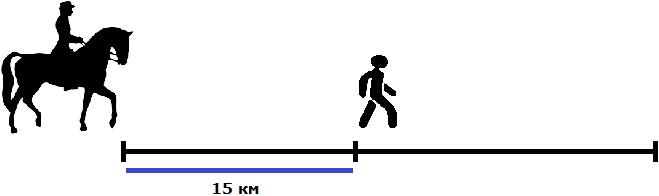
After that, the rider followed him on the road at a speed of 10 km/h. The speed of the pedestrian is only 4 km/h. This means that in some time the rider will catch up with the pedestrian. We need to find this time.
When the rider catches up with the pedestrian it will mean that they have traveled the same distance together. The distance traveled by the rider and the pedestrian is described by the following equation:
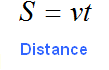
Let us use the right side of this equation to make our own equation.
The distance traveled by the rider will be described by the expression 10t. Since the pedestrian went ahead of the rider and managed to cover 15 km, the distance traveled by him will be described by the expression 4t + 15.
By the time the rider catches up with the pedestrian, they have both traveled the same distance. This allows us to equate the distances traveled by the rider and the pedestrian:
![]()
We get the simplest equation. Let's solve it:
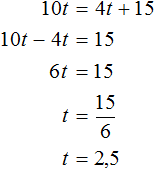
Tasks for independent decision
Solution
Train speeds in this problem are measured in kilometers per hour. Therefore, convert the 45 min specified in the problem to hours. 45 min is 0.75 h
![]()
Denote the time it takes for the freight train to arrive in the city by the variable t. Since the passenger train arrives in this city 0.75 h faster, its travel time will be denoted by the expression t − 0,75
The passenger train covered 48(t-0.75) km, and the freight train 36t km. Since we are talking about the same distance, let us equate the first expression with the second one. The resulting equation is 48(t - 0.75) = 36t. Solve it:
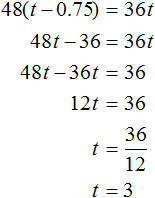
Now calculate the distance between the cities. To do this, multiply the speed of the freight train (36 km/h) by its travel time t. The value of the variable t is now known - it is equal to three hours
36 × 3 = 108 km
You can also use the speed of the passenger train to calculate the distance. But in this case the value of the variable t should be reduced by 0.75 because the passenger train spent 0.75 h less time
48 × (3 − 0,75) = 144 − 36 = 108 km
Answer: The distance between the cities is 108 km.
Solution
Let t be the time after which the cars meet. Then the first car at the time of the meeting will have traveled 65t km, and the second 60t km. Add these distances and equate them to 150. We get the equation 65t + 60t = 150
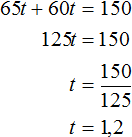
The value of the variable t is 1.2. So the cars met after 1.2 hours.
Answer: the cars met after 1.2 hours.
Solution
Let x be the number of workers in the first workshop. The second workshop had three times as many workers as the first workshop, so the number of workers in the second workshop can be denoted by the expression 3x. The third workshop had 15 fewer workers than the second workshop. Therefore, the number of workers in the third workshop can be denoted by the expression 3x - 15.
The task says that the total number of workers was 685. Therefore we can add the expressions x, 3x, 3x - 15 and equate that sum to the number 685. The result is x + 3x + (3x - 15) = 685
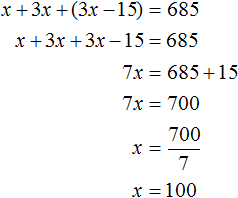
The variable x was used to denote the number of workers in the first workshop. Now we have found the value of this variable, it is 100. So there were 100 workers in the first workshop.
The second workshop had 3x workers, so 3 × 100 = 300. And the third workshop had 3x - 15, so 3 × 100 - 15 = 285
Answer: In the first shop there were 100 workers, in the second - 300, in the third - 285.
Solution
Let x motors be repaired by the first workshop. Then the second workshop had to repair 18 - x motors.
Since the first workshop fulfilled its plan by 120%, that means it repaired 1.2x motors . And the second repair shop fulfilled its plan by 125%, so it repaired 1.25(18 - x) motors.
The problem says that 22 motors were repaired. Therefore we can add the expressions 1.2x and 1.25(18 - x) , then equate that sum to the number 22. The resulting equation is 1.2x + 1.25(18 - x) = 22
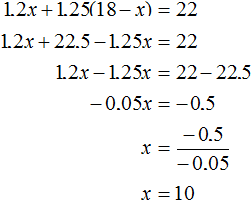
The variable x was used to denote the number of motors to be repaired by the first workshop. Now we have found the value of this variable, it is 10. So the first workshop had to repair 10 motors.
The expression 18 - x represents the number of motors to be repaired by the second workshop. So the second workshop had to repair 18 - 10 = 8 motors.
Answer: The first workshop was to repair 10 engines and the second workshop was to repair 8 engines..
Solution
Let x dollars was the price of the product before the price increase. If the price increased by 30%, it means that it increased by $0.30x dollars. After the price increase, the product began to cost $91. Add x to 0.30x and equate that sum to 91. As a result we get the equation x + 0.30x = 91
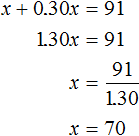
So before the price increase, the product cost $70.
Answer: Before the price increase, the product cost $70.
Solution
Let x be the initial number. Increase it by 25%. We obtain the expression x + 0.25x. Given the like terms, we obtain x + 0.25x = 1.25x.
Find what part of the original number x is from the new number 1.25x
![]()
If the new number 1.25x is 100%, and the original number x is 80% of it, then reducing the new number by 20% you can get the original number x>
![]()
Answer: to get the original number, the new number must be reduced by 20%.
Solution
Let x be the original number. Increase it by 20%. We obtain the expression x + 0.20x. Equate this sum to the number 144, so we obtain the equation x + 0.20x = 144
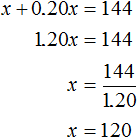
Answer: the original value of the number is 120.
Solution
Let x be the original number. Decrease it by 10%. We obtain the expression x - 0.10x. Equate this difference to the number 45, so we get the equation x - 0.10x = 45
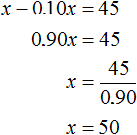
Answer: the original value of the number is 50.
Solution
Let x be the original price of the album. Decrease this price by 15%, we get x - 0.15x. Reduce the price by another $15, so we get x - 0.15x - 15. After these reductions, the album now costs $19. Equate the expression x - 0.15x - 15 to the number 19, we get the equation x - 0.15x - 15 = 19
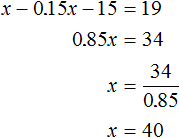
Answer: The original album price is $40.
Solution
If 80% of the mass is lost, the remaining 20% will account for 4 tons of hay. Let x tons of grass be required to produce 4 tons of hay. If 4 tons will account for 20% of the grass, then we can make the equation:
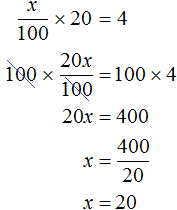
Answer: to get 4 tons of hay, you need to cut 20 tons of grass.
Solution
Let x kg of 20% salt solution be added to 1 kg of 10% salt solution.
1 kg of 10% salt solution contains 0.1 kg of salt. And x kg of 20% salt solution contains 0.20x kg of salt.
After adding x kg of the 20% solution, the new solution will contain 0.12(1 + x) kg of salt. We add 0.1 and 0.20x, then equate that sum to 0.12(1 + x). The resulting equation is 0.1 + 0.20x = 0.12(1 + x)
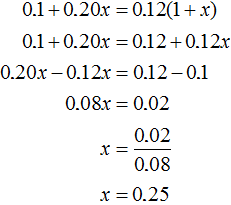
Answer: to get a 12% salt solution, you need to add 0.25 kg of 20% solution to 1 kg of 10% solution.
Solution
Let x kg of the first solution be taken. Since 25 kg of solution must be prepared, the mass of the second solution can be denoted by the expression 25 - x.
The first solution will contain 0.20x kg of salt, and the second solution will contain 0.30(25 - x) kg of salt. The resulting solution contains 25 × 0.252 = 6.3 kg of salt. Add the expressions 0.20x and 0.30(25 - x), then equate that sum to 6.3. The resulting equation is
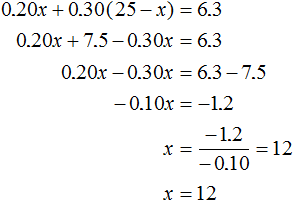
So the first solution should take 12 kg, and the second 25 - 12 = 13 kg.
Answer: the first solution should take 12 kg, and the second 13 kg.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.