Fractions is a topic that half of the world's population having difficulties with. You can't blame these people. Fractions is not an easy topic. It requires a lot of patience and attention, especially if you are studying it for the first time.
But there are good news. If you have mastered fractions, we assure you that further study of mathematics will be easy and interesting.
And if you studied the previous lesson, called division, you can be sure that you are already halfway done with fractions.
What is a fraction?
Definition. In simple terms, a fraction is a part of something. This "something" can be anything - food, money, a number. The word "fraction" also speaks for itself - it means a division.
Let's look at an example from life. We bought a pizza to eat during the day. Let's say we decide to divide it into four pieces so that we eat one piece at a time.

Look at this picture. Imagine that this is our pizza divided into four slices. Each slice of pizza is a fraction, because each slice individually is part of the pizza.
Let's say we ate one slice. How do we write it down? First a little line is drawn:
![]()
The bottom of this line records how many slices the pizza was divided into. The pizza was divided into four slices. So at the bottom of the line you write four:
![]()
And on top of this line is written how many pieces of pizza were eaten. One slice was eaten, so at the top of this line we write one:
![]()
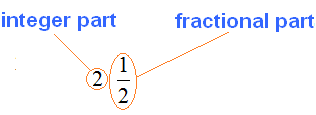
These constructions are called fractions. A fraction consists of a numerator and a denominator.
The number that is written on top is called the numerator of the fraction.
The number that is written at the bottom is called the denominator of the fraction.
In this example, the numerator of the fraction is one and the denominator of the fraction is a four. This fraction can be read as "one fourth" or "one-fourth fraction" or "one-quarter" - all of which are synonyms.
Now imagine that we ate another slice of the same pizza, which was divided into four slices. How do we write down such a fraction?
Very simple. At the top, we write 2 (since two slices have been eaten), and at the bottom, we write 4 (since there were four slices total):

This fraction reads "two fourths" or "two fourths of a fraction".
Now imagine that we didn't divide the pizza into four pieces, but into three.

Suppose we ate one slice of this pizza. How do we write down a fraction like that?
Very simple. Again a small line is drawn. At the bottom of this line we write the number 3, because the pizza is divided into three parts, and at the top of this line we write the number 1, because we ate one slice:
![]()
This fraction reads like this: "One third" or "One slice of three" or "One-third share".
If we eat two slices of pizza, this fraction is called "two thirds" and is written as follows:
![]()
Now imagine that we have divided the pizza into two parts, or as they say popularly: "In half":

Suppose we ate one of the two slices. How do we write down such a fraction?
Again we draw a line. At the bottom of this line we write the number 2, because the pizza is divided into two pieces, and at the top we write the number 1, because one piece was eaten:
![]()
This fraction reads "one half" or "one half fraction".
The slices we have now considered are called the fractions.
Definition. In general, there are two kinds of fractions: the regular fractions and decimal fractions. At this point we are looking at regular fractions. An ordinary fraction is a fraction that consists of a numerator and a denominator. We will look at decimal fractions a little later.
The denominator of a fraction is a number that shows how many equal parts something can be divided into. Let's go back to our pizza. This pizza can be divided equally into 2 parts, 3 parts, 4 parts, 5 parts, and 6 parts. Depending on how many parts we divide the pizza into, the denominator will change.
The following figure shows three pizzas that are divided differently. The first pizza has a denominator of 2. The second pizza has a denominator of 3. The third pizza has a denominator of 4.
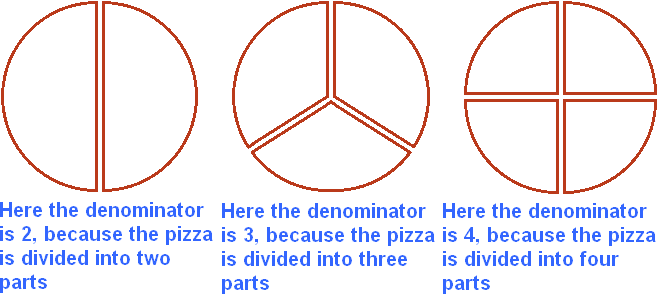
The numerator shows how many parts are taken from something. For example, if we divide a pizza into two parts, as in the first picture, and take one part for the meal, we take ![]() (one part of two), or as they say "half" of the pizza.
(one part of two), or as they say "half" of the pizza.
Using variables, the fraction can be written as follows:
![]() where a - is the numerator and b - is the denominator.
where a - is the numerator and b - is the denominator.
Definition.The next thing that is important to know is that fractions can be proper and improper.
A proper fraction is a fraction whose numerator is smaller than the denominator. For example, the following fractions are proper:
![]()
Why are these fractions called proper fractions? Recall that a fraction is a part of something. After all, it makes more sense if the fraction is smaller than where the fraction was taken from. For example, if the pizza is divided into four parts, and we take ![]() (one fourth), then our slice will be smaller than all four slices combined (than one whole pizza). This is why such fractions are called proper fractions.
(one fourth), then our slice will be smaller than all four slices combined (than one whole pizza). This is why such fractions are called proper fractions.
With an improper fraction, it's exactly the opposite. An improper fraction is a fraction where the numerator is larger than the denominator. For example, the following fractions are improper:
 You can see that these fractions have a numerator greater than the denominator. Why are these fractions called improper fractions? Recall that a fraction is a part of something. The denominator shows how many parts of something are divided into. The numerator shows how much of something was taken.
You can see that these fractions have a numerator greater than the denominator. Why are these fractions called improper fractions? Recall that a fraction is a part of something. The denominator shows how many parts of something are divided into. The numerator shows how much of something was taken.
Now take the improper fraction ![]() for example and apply it to our pizza. The denominator is 2, so the pizza is divided into two pieces, and the numerator is 9. So we took nine slices out of two. But how can you take nine slices if there are only two? The answer is no way. Therefore, such fractions are called improper fractions.
for example and apply it to our pizza. The denominator is 2, so the pizza is divided into two pieces, and the numerator is 9. So we took nine slices out of two. But how can you take nine slices if there are only two? The answer is no way. Therefore, such fractions are called improper fractions.
Fractions where the numerator and denominator are the same are also called improper. For example:
In general, such fractions should not even be called fractions. And here's why. Consider, for example, the fraction ![]() . Apply it to our pizza.
. Apply it to our pizza.
Let's say we want to eat ![]() pizzas. The denominator is 2, so the pizza is divided into two parts. And in the numerator is 2, so two parts are taken. In fact, the whole pizza is taken, and if we eat this
pizzas. The denominator is 2, so the pizza is divided into two parts. And in the numerator is 2, so two parts are taken. In fact, the whole pizza is taken, and if we eat this ![]() pizza, we are not eating part of the pizza, but the whole pizza. In other words, eat not a fraction, but a whole fraction of a pizza. Therefore, a fraction with the same numerator and denominator is called an improper fraction.
pizza, we are not eating part of the pizza, but the whole pizza. In other words, eat not a fraction, but a whole fraction of a pizza. Therefore, a fraction with the same numerator and denominator is called an improper fraction.
Fraction means division
The line in the fraction that separates the numerator from the denominator means division. It says that the numerator can be divided by the denominator.
For example, consider the fraction![]() . The fractional line says that a four can be divided by a two. We know that four divided by two is two. Put an equal sign (=) and write down the answer:
. The fractional line says that a four can be divided by a two. We know that four divided by two is two. Put an equal sign (=) and write down the answer:

We can conclude that any division of numbers can be written using fractions. For example:

These are the simplest examples. You can see that they don't have a remainder. The remainder is a little more complicated, but it is more interesting. Let's talk about this in the next topic, which is called "calculating the whole part of a fraction.
Calculating the whole part of a fraction
Calculate the fraction![]() . Five divided by two will be two and one in the remainder:
. Five divided by two will be two and one in the remainder:
5 : 2 = 2 (1 in the remainder)
Verification: (2 × 2) + 1 = 4 + 1 = 5
But now we are dealing with fractions, so we have to answer in fractional form. To get a good understanding of how to do this, let's look at an example from life.
Imagine you have five apples and decide to share them with your friend. And share them fair and square, so that everyone gets the same. How do you divide these five apples?
Obviously, each of you will get two apples, and you will cut the remaining one apple in half with a knife and divide it among yourselves as well:
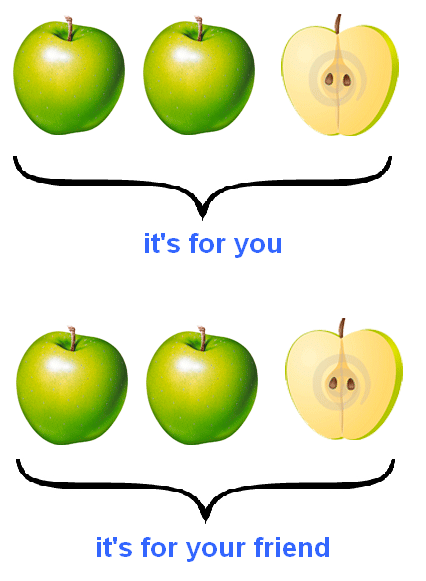
Look carefully at this picture. It shows how the five apples are divided between you and your friend. Obviously, everyone got two whole apples and a half of an apple.
Now go back to the fraction ![]() and answer her question. Whats the result of division? We look at our picture and answer: if five apples are divided by two, each of them will get two whole apples and a half of an apple. Let's write it down this way:
and answer her question. Whats the result of division? We look at our picture and answer: if five apples are divided by two, each of them will get two whole apples and a half of an apple. Let's write it down this way:

Schematically it looks like this:
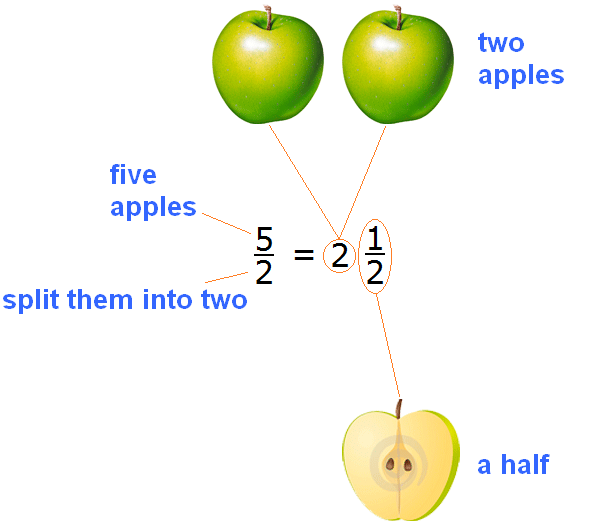
The procedure we have just performed is called the extraction of the whole part of the fraction.
In our example, we extracted the whole part of the fraction ![]() and got a new fraction
and got a new fraction ![]() . Definition. Such a fraction is called a mixed fraction. A mixed fraction is a fraction that has an whole part and a fractional part.
. Definition. Such a fraction is called a mixed fraction. A mixed fraction is a fraction that has an whole part and a fractional part.
In our example, the whole part is 2 and the fractional part is![]()
Be sure to memorize these concepts! Better yet, write them down in your workbook.
The whole part can only be extracted from improper fractions. Recall that an improper fraction is a fraction with a numerator greater than the denominator. For example, the following fractions are improper and have the whole part highlighted:

To isolate the whole part, it is enough to know how to divide numbers by an long division method. For example, select the whole part of a fraction ![]() . Write this expression in the corner and solve it:
. Write this expression in the corner and solve it:

After solving the example is completed, the new fraction is assembled like a child's constructor. It is important to understand where to put the fraction. The quotient goes to the whole part, the remainder goes to the numerator of the fractional part, and the divisor goes to the denominator of the fractional part.
In principle, if you know the multiplication table well, and can quickly perform elementary calculations in your head, you can do without writing in the corner. In schools, by the way, this is exactly what they require - that students should not waste time on simple operations, but immediately write down the answers.
But if you're just starting to learn math, we advise you to write down every little detail.
Consider another example of whole part extraction. Suppose we need to select the whole part of a fraction ![]()
Write this expression in the corner and solve it. Then we assemble the mixed fraction:

Got it: 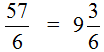
Conversion of a mixed number into an improper fraction
Any mixed number is the result of isolating the whole part in an improper fraction. For example, consider an improper fraction ![]() . If you isolate the whole part of it, you get
. If you isolate the whole part of it, you get ![]()
![]()
But the reverse process is also possible: any mixed number can be converted into an improper fraction. To do this, multiply the whole part by the denominator of the fractional part and add the result to the numerator of the fractional part. The result will be the numerator of the new fraction, and the denominator will remain unchanged.
For example, let's convert a mixed number ![]() into an improper fraction. Multiply the whole part of 2 by the denominator of the fractional part:
into an improper fraction. Multiply the whole part of 2 by the denominator of the fractional part:
2 × 3 = 6
Then add the numerator of the fractional part to 6:
6 + 1 = 7
The resulting seven will be the numerator of the new fraction, and the denominator 3 will remain unchanged:
![]()
The detailed solution looks like this:
![]()
And with the help of variables, the convertion of a mixed number into an improper fraction can be written as follows:
![]()
Example 2. Convert a mixed number ![]() into an improper fraction.
into an improper fraction.
Multiply the whole part of the mixed number by the denominator of the fractional part and add to the numerator of the fractional part, and leave the denominator unchanged:
![]()
Basic property of fractions
Definition. The basic property of fractions is that if the numerator and denominator of a fraction are multiplied or divided by the same number, so the fraction will be equal to it. This means that the value of the fraction will not change.
For example, consider a fraction ![]() . Multiply its numerator and denominator by the same number, for example number 2
. Multiply its numerator and denominator by the same number, for example number 2
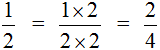
We got a new fraction ![]() . If we believe the basic property of fractions, then fractions
. If we believe the basic property of fractions, then fractions ![]() and
and ![]() are equal to each other. Is this true? Let's check by drawing these fractions as slices of pizza:
are equal to each other. Is this true? Let's check by drawing these fractions as slices of pizza:

Look closely at these two pictures. The first figure illustrates a fraction ![]() (one piece of two), and the second illustrates the fraction
(one piece of two), and the second illustrates the fraction ![]() (two pieces of four). If you take a good look at these pieces, you will see that they are the same size. The only difference is that they are cut differently. The first pizza was cut into two slices and one slice was taken from it. The second pizza was cut into four slices and two slices were taken from it.
(two pieces of four). If you take a good look at these pieces, you will see that they are the same size. The only difference is that they are cut differently. The first pizza was cut into two slices and one slice was taken from it. The second pizza was cut into four slices and two slices were taken from it.
Therefore, we can put an equal sign (=) between fractions ![]() and
and ![]() because they are equal to the same value:
because they are equal to the same value:
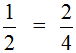
Now let's test the basic property of fractions by dividing the numerator and denominator by the same number.
Consider a fraction ![]() . Let's divide its numerator and denominator by the same number, for example the number 2
. Let's divide its numerator and denominator by the same number, for example the number 2
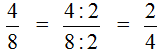
We got a new fraction ![]() . If we believe the basic property of fractions, then fractions
. If we believe the basic property of fractions, then fractions ![]() and
and ![]() are equal to each other. Is this true? Let's check by drawing these fractions as slices of pizza:
are equal to each other. Is this true? Let's check by drawing these fractions as slices of pizza:

Look closely at these two pictures. The first figure illustrates a fraction ![]() (four pieces out of eight), and the second illustrates the fraction
(four pieces out of eight), and the second illustrates the fraction ![]() (two pieces of four). If you take a good look at these pieces, you will see that they are the same size. The only difference is that they are cut differently. The first pizza was cut into eight slices, and four slices were taken from it. The second pizza was cut into four slices and two slices were taken from it.
(two pieces of four). If you take a good look at these pieces, you will see that they are the same size. The only difference is that they are cut differently. The first pizza was cut into eight slices, and four slices were taken from it. The second pizza was cut into four slices and two slices were taken from it.
Therefore, we can put an equal sign (=) between fractions ![]() and
and ![]() because they are equal to the same value:
because they are equal to the same value:
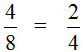
Now we have fully tested how the basic property of fractions works, and we are convinced that it works great.
The number by which the numerator and denominator are multiplied is called the additional multiplier. Make sure you remember that!
Simplifying fractions
Fractions can be simplified. To reduce means to make a fraction shorter and easier to understand. For example, a fraction![]() looks much simpler and prettier than
looks much simpler and prettier than ![]() .
.
If you get a big fraction when you solve the examples, you should try to reduce it.
Fraction reduction relies on the basic property of fractions. Therefore, before learning how to reduce fractions, be sure to learn the basic property of fractions.
Dividing the numerator and denominator by their greatest common divisor is called fraction reduction or simplification.
Example 1. Simplify a fraction ![]()
So, we need to divide the numerator and denominator of the fraction![]() on the greatest common divisor of 2 and 4.
on the greatest common divisor of 2 and 4.
In this case, the fraction is simple and its GCD is easy to find. The GCD of 2 and 4 is 2. Therefore, the numerator and denominator of the fraction ![]() must be divided by 2
must be divided by 2
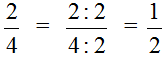
As a result, the fraction ![]() has become a simpler fraction
has become a simpler fraction ![]() . The value of the original fraction did not change, because reduction involves dividing the numerator and denominator by the same number. And this action, as stated earlier, does not change the value of the fraction.
. The value of the original fraction did not change, because reduction involves dividing the numerator and denominator by the same number. And this action, as stated earlier, does not change the value of the fraction.
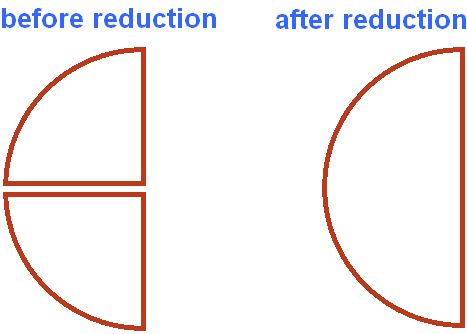
The figure shows fractions ![]() and
and ![]() as slices of pizza. Before the reduction and after the reduction they have the same size. The only difference is that they are cut differently.
as slices of pizza. Before the reduction and after the reduction they have the same size. The only difference is that they are cut differently.
Example 2. Let's reduce the fraction ![]()
To reduce the fraction![]() , you need to divide the numerator and denominator of this fraction by the greatest common divisor of the numbers 20 and 40.
, you need to divide the numerator and denominator of this fraction by the greatest common divisor of the numbers 20 and 40.
The GCD of 20 and 40 is 20. Therefore, divide the numerator and denominator of fraction![]() by 20
by 20
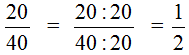
Example 3. Let's reduce the fraction ![]()
To reduce the fraction![]() , you need to divide the numerator and denominator of this fraction by the greatest common divisor of 32 and 36.
, you need to divide the numerator and denominator of this fraction by the greatest common divisor of 32 and 36.
The GCD of 32 and 36 is number 4. Therefore, divide the numerator and denominator of the fraction ![]() by 4
by 4
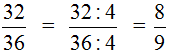
If there are prime numbers in the numerator and denominator, the fraction cannot be reduced - it is not reduced. Such fractions are called irreducible. For example, the following fractions are irreducible:
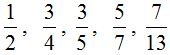
Recall that prime numbers are numbers that are divided only by one and themselves.
The second way to reduce fractions
The second method is a short version of the first method. Its essence is that a detailed explanation of what the numerator and denominator were divided into is omitted.
For example, let's return to fractions ![]() . We reduced this fraction by 4, that is, we divided the numerator and denominator of this fraction by the number 4
. We reduced this fraction by 4, that is, we divided the numerator and denominator of this fraction by the number 4
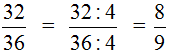
Now imagine that this expression does not contain the construction ![]() , and immediately recorded the answer
, and immediately recorded the answer ![]() . You get the following expression:
. You get the following expression:
![]()
The point is that the number by which the numerator and denominator are divided is kept in mind. In our case, the numerator and denominator divide by 4 - this is the number we will store in our mind.
First divide the numerator by the number 4. The answer is written next to the numerator, crossing it out:
![]()
Then divide the denominator by 4 in the same way. Write the answer next to the denominator, crossing it out beforehand:
![]()
Then we assemble a new fraction. In the numerator we send a new number 8 instead of 32, and in the denominator we send a new number 9 instead of 36
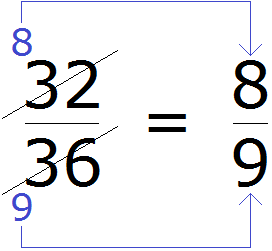
A kind of replacement of one fraction with another takes place. The value of the new fraction equals the value of the previous fraction, because the basic property of fractions works, which says that if the numerator and denominator of a fraction are multiplied or divided by the same number, we get a fraction equal to it.
Also, fractions can be reduced by first decomposing the numerator and denominator into prime factors.
For example, let's reduce a fraction ![]() , by first decomposing the numerator and denominator into prime factors:
, by first decomposing the numerator and denominator into prime factors:
![]()
So, we decomposed the numerator and denominator of the fraction ![]() into multipliers. Now we apply the second method of reduction. In the numerator and in the denominator select a factor and divide the selected factors by the GCD of these factors.
into multipliers. Now we apply the second method of reduction. In the numerator and in the denominator select a factor and divide the selected factors by the GCD of these factors.
Let's reduce each triplet in the numerator and denominator. To do this, divide these triples by 3 (by their greatest common divisor). We obtain the following expression:

You can also cut down on the three in the numerator and denominator:

There is nothing else to reduce. The last three in the denominator cannot be simply reduced, because there is no factor in the numerator that can be reduced together with this three.
Write a new fraction with new multipliers in the numerator and denominator.
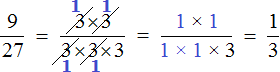
We got the answer ![]() . So, when reducing a fraction
. So, when reducing a fraction ![]() you get a new fraction
you get a new fraction ![]() .
.
It is not recommended to use the second method of reduction of fractions and the method of expansion into simple multipliers of the numerator and denominator, if a person is just beginning to learn mathematics. Practice shows that this proves to be difficult at first stages.
So if you have trouble using the second method, use the good old method of reduction: divide the numerator and denominator of the fraction by their greatest common divisor. The expression in this case is simple, clear, and beautiful. For example, the previous example can be solved the old way and will look like this:
![]()
Compare this expression with the expression we got when we used the second method:
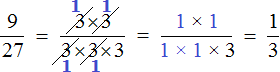
The first expression is much clearer, neater, and shorter. Isn't it?
Exercises
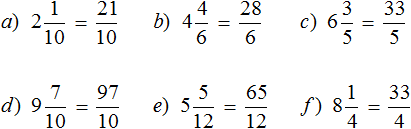










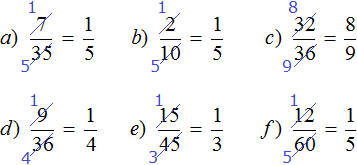













Comments
You might also want to consider hiding what’s further down the page as for some people when they see too much in front that can be too depressing to get started. Breaking the learning into smaller steps where you only see and tackle the immediate step in front of you becomes easier to remain motivated.
Hope this helps.