In previous lessons, it was said that a fraction consisting of a whole part and a fractional part is called a mixed number.
All fractions that have a whole part and a fraction part have one common name: mixed numbers.
Mixed numbers can be added, subtracted, multiplied, and divided, just like proper fractions. In this lesson we will look at each of these operations separately.
Adding whole number to a fraction
You may encounter problems in which you need to add a whole number and a fraction. For example, add a number 2 and a fraction 
. To solve this example, you need to represent the number 2 as a fraction 
. Then add fractions with different denominators:
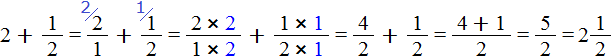
Now look carefully at this example. Let's look at the beginning and the end of it. Its beginning looks like this: 
, and the end is this: 
. The difference is that in the first case the number 2 and the fraction are joined by an addition sign, and in the second case they are written together. In fact, this is the same thing. The point is that is a convolute form of a mixed number, and is an expanded form.
When we have a mixed number of the form in front of us, we must realize that the addition sign is omitted.
What conclusion can be drawn? If you need to add a number to a proper fraction, you can omit the plus sign and write the whole number and fraction together.
So the value of the expression is
If you add half a pizza to two whole pizzas, you get two whole pizzas and half a pizza:
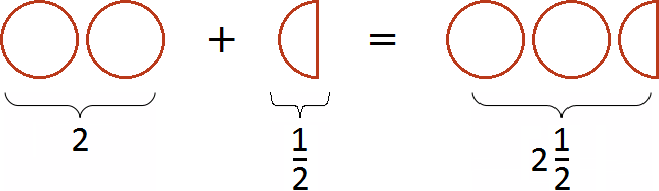
Example 2. Find the value of the expression 
Let's represent the number 3 as a fraction of 
. Then add fractions with different denominators:
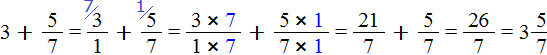
This is the first way. The second way is much easier. You can put an equal sign and write the whole part and the fractional part together. That is, omit the addition sign:
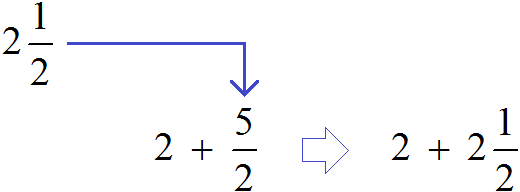
Example 3. Find the value of the expression 
You can write the number 2 and the fraction 
together, but that answer will not be final because you can separate the whole part in the fraction .
Therefore, in this example, you must first isolate the whole part in the fraction . Five second fractions are two integers and one second:
Now, in the main expression we write the mixed number instead of the fraction
We have a new expression 
. In this expression, write the mixed number in expanded form:
Apply the combinative law of addition. If we add two twos, we get 4:
Now let's roll up the resulting mixed number:
This is the final answer. The detailed solution of this example can be written as follows:
Adding mixed numbers
There are problems in which you need to add mixed numbers. For example, to find the value of the expression 
. To solve this example, you need to add the whole and fractional parts separately.
First, let's write down the mixed numbers in expanded form:
Apply the combinative law of addition. Group the whole and fractional parts separately:
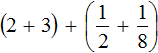
Let's calculate the integers: 2 + 3 = 5. In the main expression, replace the expression in parentheses (2 + 3) with the resulting five:
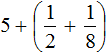
Now let's calculate the fractional parts. This is the addition of fractions with different denominators. We already know how to add such fractions:
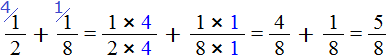
We got 
. Now in the main expression 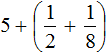replace the fractional parts with the resulting fraction .
Now let's collapse the resulting mixed number:
Thus, the value of the expression is 
. Let's try to represent this solution in the form of a picture. If you add three whole pizzas and an eighth to two whole pizzas and a half, you get five whole pizzas and five eighths of pizzas:
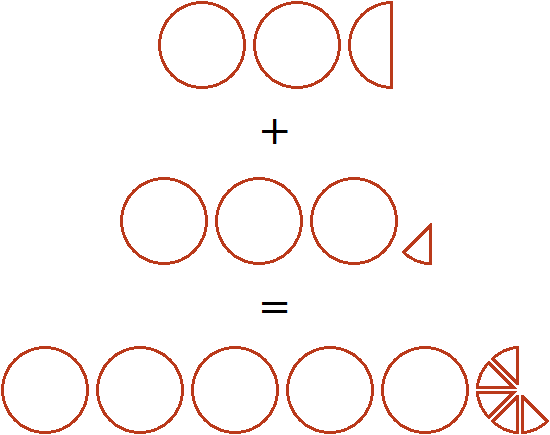
Examples like this need to be solved quickly, without stopping for details. If we were in school, we would have to write down the solution to this example as follows:
If you see such a short solution in the future, don't be frightened. You already understand where it came from.
Example 2. Find the value of the expression 
Let's write the mixed numbers in expanded form:
Let's group the integers and fractions separately:
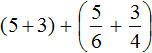
Let's calculate the integers: 5 + 3 = 8. In the main expression, replace the expression in parentheses (5 + 3) with the resulting number 8
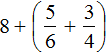
Now let's calculate the fractional parts:
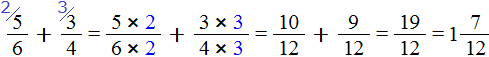
We obtained a mixed number of 
. Now replace the expression in parentheses in the main expression 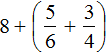with the resulting mixed number
We got the expression . In this case, the number 8 must be added to the whole part of the mixed number . To do this, the mixed number can be temporarily expanded to make it clearer what to add to what:
Let's add the whole parts. We get 9
We wrap up the finished answer:
Thus, the value of the expression is 
.
The complete solution of this example is as follows:
There is a universal rule for solving such examples. It looks like this:
To add up mixed numbers, you have to:
- reduce the fractional parts of these numbers to a common denominator;
- perform addition of integers and fractions separately.
If adding fractions results in an improper fraction, isolate the whole part of the fraction and add it to the resulting whole.
The use of ready-made rules is acceptable if the essence of the topic is fully understood. A formulaic solution, looking at other similar examples, leads to errors that take extra time to find. Therefore, it is more reasonable to understand the topic first, and then use a ready-made rule.
Example 3. Find the value of the expression 
Let's use a ready-made rule. Let's reduce the fractional parts to a common denominator, then add the whole and fractional parts separately:
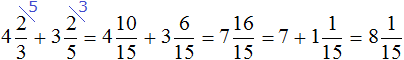
Adding whole and mixed numbers
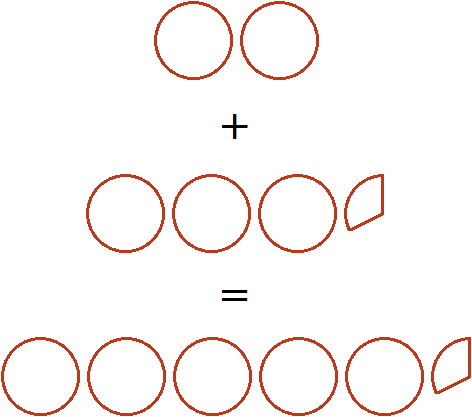
You may encounter problems where you need to add a whole and a mixed number. For example, add 2 and a mixed number 
. In this case, the whole parts are added separately, and the fractional part is left unchanged:
Here the mixed fraction was expanded as part of the solution, then the whole parts were grouped and added together. At the end the whole and fractional parts were folded. The result was the answer 
.
Let's try to represent this solution in the form of a picture. If you add three whole pizzas and a third of a pizza to two whole pizzas, you get five whole pizzas and a third of a pizza:
Example 2. Find the value of the expression 
In this example, as in the previous one, you have to add up the whole parts:
The whole part and the fractional part remain to be rolled up, but the thing is that the fractional part of 
is an improper fraction. First, we need to isolate the whole part in this improper fraction. Then add the whole part of that fraction to 4, and leave the fractional part unchanged. Let's continue this example on a new line:
Subtracting a fraction from a whole number
You may encounter problems in which you want to subtract a fraction from a whole number. For example, subtract fraction from number 1. To solve such an example, imagine the whole 1 as a fraction 
, and subtract fractions with different denominators:
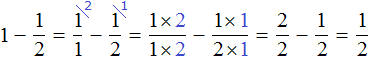
If there is one whole pizza and we subtract half a pizza from it, we have half a pizza:
Example 2. Find the value of the expression 
.
Let's represent the number 2 as a fraction 
, and subtract fractions with different denominators:
If there are two whole pizzas and we subtract half from the bottom, that leaves one whole pizza and half:
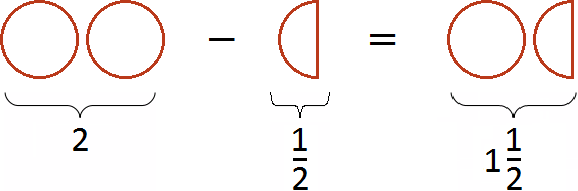
Such examples can be solved in your mind. It is enough to be able to reproduce them in your imagination. For example, let's find the value of 
without doing any calculations on paper.
Let's pretend that the number 3 is three pizzas:
We need to subtract 
from them. We remember that a third is as follows:
Now imagine what three pizzas would look like if you cut off that third of them
It came out 
(two whole and two thirds of a pizza).
To see if the solution is correct, you can find the value of the expression by the usual method, presenting the number 3 as a fraction, and subtracting fractions with different denominators:
Example 3. Find the value of the expression 
Let's represent the number 3 as a fraction 
. Then subtract fractions with different denominators:
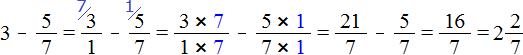
Subtracting a mixed number from a whole number
Now we are ready to subtract a mixed number from a whole number. Let's find the value of the expression 
.
To solve this example, the number 5 must be presented as a fraction, and the mixed number 
must be converted into an improper fraction. After converting the mixed number into an improper fraction, we obtain a fraction 
. Now subtract fractions with different denominators:
If you subtract one whole pizza and one half pizza from five whole pizzas, you are left with three whole pizzas and one half pizza:
Example 2. Find the value of the expression 
Let us represent 6 as a fraction 
, and the mixed number 
as an improper fraction. After converting the mixed number to an improper fraction, we obtain a fraction 
. Now subtract fractions with different denominators:
Examples on subtracting fractions from a number or subtracting mixed fractions from a number can again be done in the mind. This process is easy to imagine.
For example, if you need to quickly find the value of the expression 
, it is not necessary to represent the number 2 as a fraction and subtract fractions with different denominators. You can imagine the number 2 as two whole pizzas and then imagine cutting two thirds from one of them (two slices out of three).
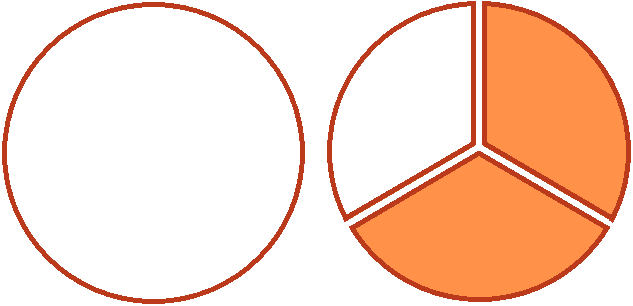
That leaves of the pizza that was cut off 
of it. Plus one of the pizzas will remain intact. That would make one whole pizza and one-third of a pizza:
If you cover two-thirds of the pizza with your hand in the picture (it's shaded), you'll know right away.
Subtracting mixed numbers
There are problems where you need to subtract one mixed number from another mixed number. For example, find the value of the expression: 
To solve this example, convert the mixed numbers 
and 
to improper fractions, then subtract fractions with different denominators:
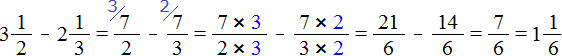
If you subtract two whole pizzas and a third of a pizza from three whole pizzas, you are left with one whole pizza and one sixth of a pizza:
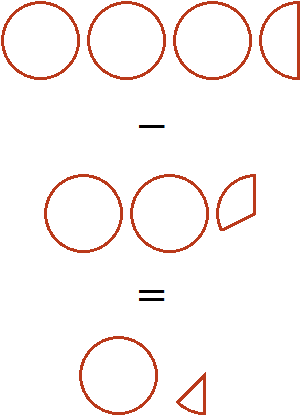
Example 2. Find the value of the expression 
Convert the mixed numbers 
and 
into improper fractions and subtract fractions with different denominators:
We'll come back to the subtraction of mixed numbers. There are many subtleties in subtracting fractions that a beginner is not yet prepared for. For example, it is possible that the minuend may be less than the subtrahend. This can lead us into the world of negative numbers, which we haven't yet studied.
In the meantime, we will study multiplication of mixed numbers. It is not as complicated as addition and subtraction.
Multiplying fractions by whole numbers
Any whole number can be multiplied by a fraction. All you have to do is multiply the number by the numerator of the fraction.
For example, multiply the number 5 by a fraction . To solve this example, multiply the number 5 by the numerator of the fraction
The answer is an improper fraction. Let's separate the whole part of the fraction:
If there are five whole pizzas and we take half of that number, we have two whole pizzas and half a pizza:
Example 2. Find the value of the expression 
Multiply the number 3 by the numerator of the fraction 
The answer is an improper fraction 
, but we extracted the whole part of it and got 2.
Also, you could have shortened the fraction. The result would have been the same. It would look like this:
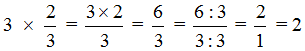
If there are three whole pizzas and we take two thirds of that amount, we have two whole pizzas:
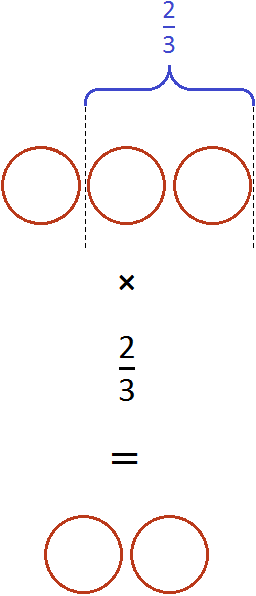
Example 3. Find the value of the expression 
This example is solved in the same way as the previous ones. The whole and the numerator of the fraction must be multiplied:
Example 4. Find the value of the expression 
Multiply the number 3 by the numerator of the fraction
Multiplying mixed numbers and fractions
To multiply a mixed number by a fraction, you must convert the mixed number to an improper fraction, then multiply the proper fractions.
Example 1. Find the value of the expression 
Convert the mixed number 
into an improper fraction. After translation, the number will become a fraction of 
. Then we can multiply that fraction by
Let's say there is one whole pizza and a half pizza:
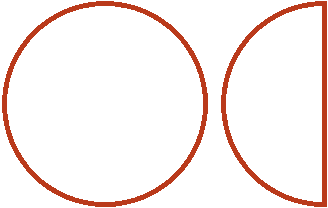
To multiply these pieces by is to take two-thirds of them. To take two-thirds of them, first divide them into three equal parts. Split in half the pizza on the left. Then we have three equal slices:
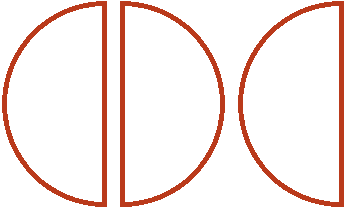
Now if we take (two slices of the three available), we get one whole pizza. For clarity, let's paint over the two slices:
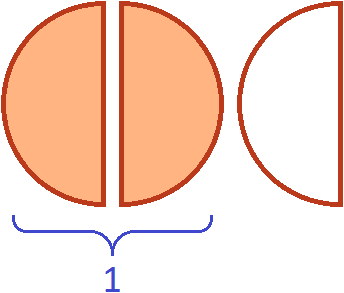
Therefore, the value of the expression was 1
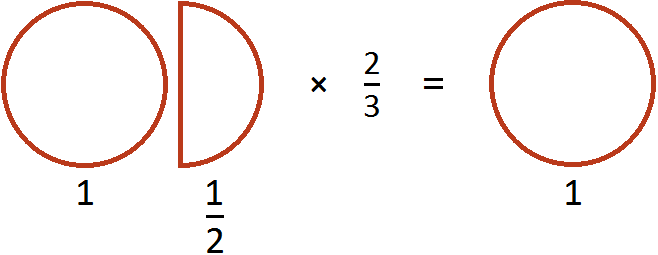
Multiplying mixed numbers
There are problems that require you to multiply mixed numbers. For example, multiply and . To solve this example, you must convert these mixed numbers to improper fractions, then multiply the improper fractions:
Let's try to understand this example with the help of a picture. Let's say there is one whole pizza and one half of a pizza:
Now let's deal with the mixed multiplier of . This multiplier means that one whole and half pizza must be taken 2 times and another times.
The multiplier 2 is clear: it means that one whole pizza and one half pizza must be taken twice. Let's take two whole pizzas and two halves:
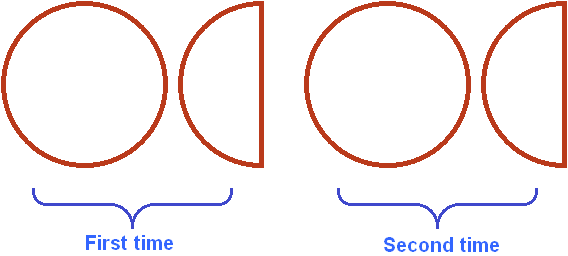
But we still have of the original whole pizza and half, because the multiplier was a mixed number of . To do this, go back to the original one whole pizza and half pizza, and divide them into equal parts so that we can take exactly half of them. And we can take half if we divide the whole pizza into four parts, and the half into two parts:
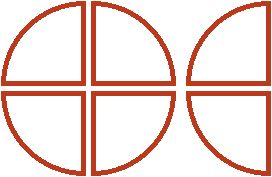
We have divided our whole pizza and half into equal pieces, and now we can say what is half of those pieces. Half of those slices is 
of a pizza. This can be clearly seen if we arrange our equal slices as follows:
And if you look at the original whole pizza and the half in terms of such an order as in this picture, the half of them is of the pizza.
Therefore, the value of the expression 
is 
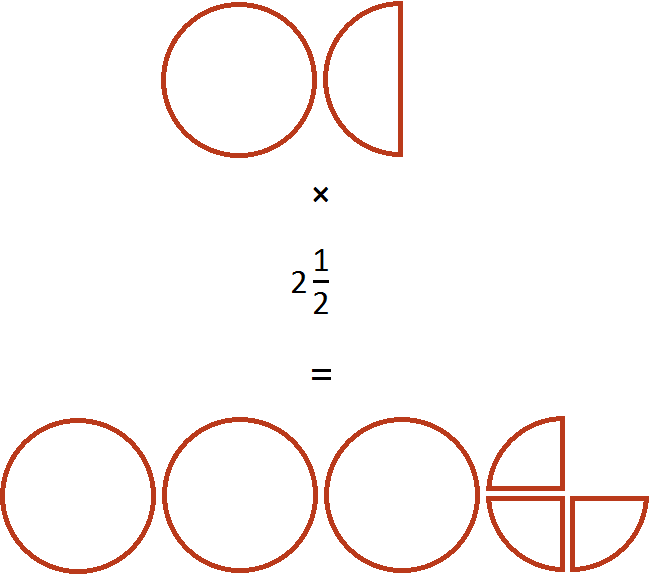
Example 2. Find the value of the expression 
Convert the mixed numbers into improper fractions and multiply those improper fractions. If the answer is an improper fraction, select the whole part of the fraction:
Dividing a whole number by a fraction
To divide a whole number by a fraction, multiply the whole by the inversed fraction.
For example, divide the number 3 by a fraction . Here the number 3 is the divisor and the fraction is the divisor.
To solve this example, multiply the number 3 by a fraction that is the inverse of a fraction . And the inverse of fraction is 
. Therefore, multiply 3 by the fraction .
Let's say there are three whole pizzas:
If we ask the question "how many times (half a pizza) is contained in three pizzas", the answer is "six times".
Indeed, if we divide each pizza in half, we have six halves:
Therefore, the value of the expression 
is 6.
Example 2. Find the value of the expression 
To solve this example, you need to multiply the number 2 by a fraction that is the inverse of the fraction . And the inverse of a fraction of is .
Let's say there are two whole pizzas:
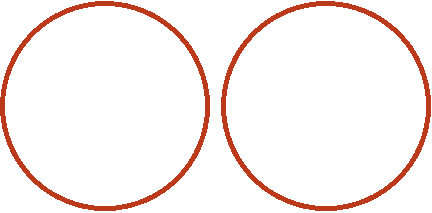
Let's ask the question, "How many times pizzas are in these two pizzas?" To answer this question, isolate the whole part in the fraction . After singling out the whole part of the fraction, we get
Now let's put the question this way, "How many times (one whole and one half pizza) is contained in two pizzas?"
To answer this question, find the number of pizzas in the two pizzas shown in the following picture:
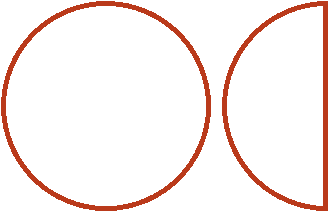
Two pizzas contain one whole pizza and one half pizza. This can be seen if the second pizza is cut in half:
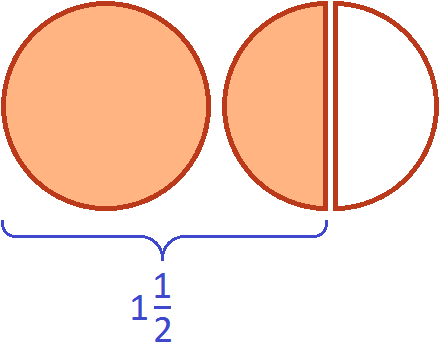
And the remaining half is a third of the that didn't fit. The reason it is a third is because in one whole and one half of the pizza, the whole portion of the pizza can be divided in half. Then each slice would be a third of that amount:
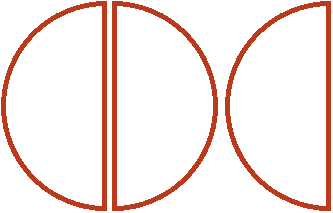
Therefore, the value of the expression is 
Example 3. Find the value of the expression 
To solve this example, you need to multiply the number 5 by the inverse of the fraction 
. And the inverse of a fraction is a fraction 
. Therefore, multiply 5 by .
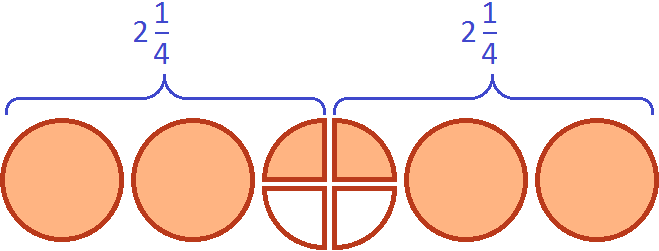
A fraction of is two whole pizzas and 
. Simply put, two whole fractions and a quarter of a pizza:
And the expression determines how many times 
is contained in five whole pizzas. The answer was a mixed number of 
.
That is, of a pizza is contained in five whole pizzas times.
Let's fumble in five pizzas two times
There are two quarters left out in white. These two quarters represent 
of the that didn't fit. The reason they are two nines is because in a pizza, each whole pizza can be divided into four pieces. Then each slice would be a ninth of that amount, and two slices would be respectively two of the nine:
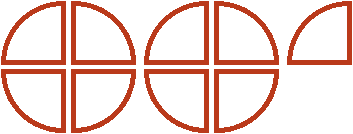
Therefore, the value of the expression is
Dividing a fraction by a whole number
To divide a fraction by a whole number, multiply the fraction by the inverse of the divisor. We did this kind of division in the last lesson. Let's go over it again.
Example 1. Divide fraction by number 2
To divide a fraction by 2, multiply the fraction by the inverse of 2. The inverse of 2 is fraction
Let there be half a pizza:
Let's divide it equally into two parts. Then each part will be one-fourth of a pizza:
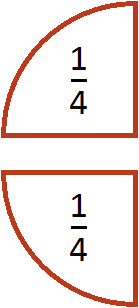
Therefore, the value of the expression 
is
Example 2. Find the value of the expression 
To solve this example, multiply the fraction 
by the inverse of 2. The inverse of 2 is fraction
Example 3. Find the value of the expression 
Multiply the first fraction 
by the inverse of 3. The inverse of 3 is fraction
Dividing a whole number by a mixed number
You may encounter problems that require dividing a whole number by a mixed number. For example, divide 2 by .
To solve this example, convert the divisor to an improper fraction. Then multiply the number 2 by the fraction inverse of the divisor.
Convert the divisor of to an improper fraction, you get . Then multiply 2 by the fraction inverse of the fraction . The inverse of fraction is fraction
Let's say there are two whole pizzas:
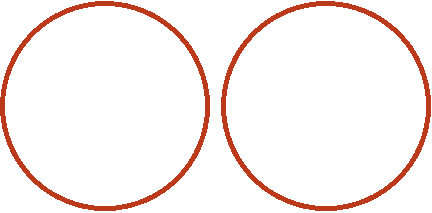
Ask the question, "How many times (one whole and one half pizza) are in two whole pizzas?" We solved a similar example earlier when we learned how to divide a whole number by a fraction.
Two pizzas contain one whole pizza and one half pizza. This can be seen if the second pizza is cut in half:
And the remaining half is a third of the that didn't fit. The reason it is a third is because in one whole and one half of the pizza, the whole portion of the pizza can be divided in half. Then each slice would be a third of that amount:
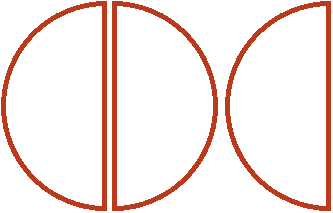
Therefore, the value of the expression 
is
Example 2. Find the value of the expression 
Convert the divisor of 
into an improper fraction, and you get 
. Now multiply the number 5 by the inverse of the fraction . The inverse of the fraction is fraction 
First, we got the answer 
, then we reduced this fraction by 5, and got 
, but we were not satisfied with this answer either, because it was an improper fraction. We singled out the whole part of this improper fraction. As a result, we got the answer 
Dividing a mixed number by a whole number
To divide a mixed number by a whole number, you must convert the mixed number into an improper fraction, then multiply that fraction by the number inverse of the divisor.
For example, divide by 2. To solve this example, convert the divisor of to an improper fraction. Then multiply that fraction by the number inverse of the divisor 2.
Convert the mixed number into an improper fraction, you get .
Now multiply by the inverse of 2. The inverse of 2 is a fraction of
Let's say there is one whole pizza and a half pizza:
Divide this amount of pizza equally into two parts. To do this, first divide a whole pizza into two parts:
Then divide equally into two parts and half:
Now if we group these slices into two groups, we get of a pizza in each group:
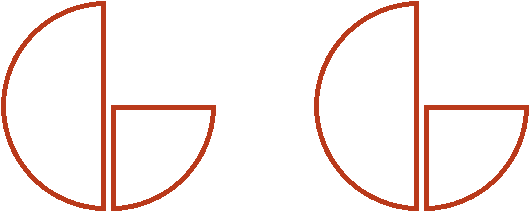
Therefore, the value of the expression 
is
Example 2. Find the value of the expression 
Convert the divisor of 
into an improper fraction, you get 
. Now multiply by the inverse of 4. The inverse of 4 is a fraction of 
.
Dividing mixed numbers
To divide mixed numbers, you need to convert them into improper fractions, then do the usual division of fractions. That is, multiply the first fraction by the inversed second fraction.
Example 1. Find the value of the expression 
Let's convert the mixed numbers into improper fractions. We obtain the following expression:
We already know how to solve this problem. The first fraction must be multiplied by the inverse of the second fraction. The inverse of the second fraction is fraction 
.
Let's finish this example to the end:
Let's say there are two whole and half pizzas:
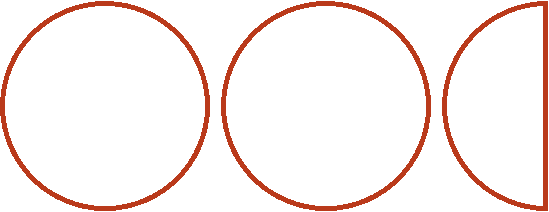
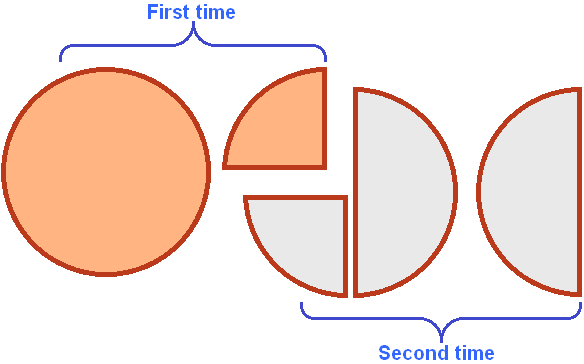
If we ask the question "How many times 
(one whole and one quarter pizza) is in two whole and one half pizza", the answer is "two times":
Example 2. Find the value of the expression 
Let's convert the mixed numbers into improper fractions. We obtain the following expression:
Now multiply the first fraction by the inverse of the second fraction. The inverse of the fraction is the fraction
First, we got a fraction 
. We reduced this fraction by 9. As a result, we got a fraction 
, but we were not satisfied with this answer either, so we separated the whole part from the fraction . As a result, we got the final answer 
.
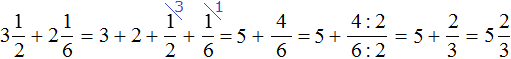
Comments