Decimals can be added, subtracted, multiplied, and divided. Decimals can also be compared to each other.
In this lesson we will look at each of these operations separately.
Adding decimals
As we know, a decimal consists of a whole part and a fractional part. When adding decimals, the whole and fractional parts are added separately.
For example, let's add the decimals 3.2 and 5.3. It is more convenient to add decimals in columns.
Let's first write these two fractions in a column, making sure the whole parts are under the whole parts and the fractional parts are under the fractional parts. At school, this requirement is called "dot under dot".
Let's write the fractions in a column so that the decimal point is under the point:

Add up the fractional parts: 2 + 3 = 5. Write five in the fractional part of our answer:
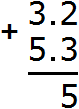
Now add the whole parts: 3 + 5 = 8. Write the eight in the whole part of our answer:
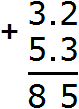
Now separate the whole part from the fractional part with a dot. To do this, again follow the rule "dot under dot":
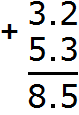
The answer is 8.5. So the expression 3.2 + 5.3 equals 8.5
3.2 + 5.3 = 8.5
In fact, not everything is as simple as it seems at first glance. Here, too, there are pitfalls, which we are now going to talk about.
Place value with decimals
Decimals, like regular numbers, have their own digits. These are the digits of tenths, digits of hundredths, and digits of thousandths. In this case, the digits begin after the point.
The first digit after the point is the decimal place, the second digit after the point is the hundredth place, and the third digit after the point is the thousandth place.
Digits in decimals store some useful information. In particular, they tell you how many tenths, hundredths, and thousandths there are in a decimals.
For example, consider the decimal 0.345
The position where the triple is located is called the digit of tenths
The position where there is a four is called the hundredths digit
The position where there is a five is called the digit of thousandths
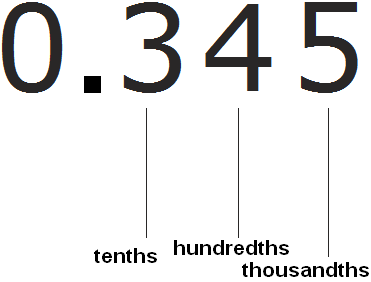
Let's look at this picture. We see that there is a three in the decimal place. This tells us that the decimal 0.345 contains three tenths of ![]() .
.
Let's see further. In the hundredths digit there is a four. This indicates that the decimal 0.345 contains four hundredths of ![]() .
.
Let's see further. In the thousandth digit is a five. This indicates that the decimal 0.345 contains five thousandths of ![]() .
.
If we add the fractions![]() ,
, ![]() and
and ![]() , we get the original decimal 0.345
, we get the original decimal 0.345
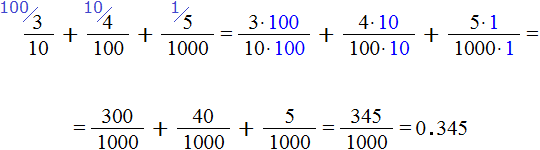
At first we got the answer ![]() , but we converted it to a decimal and got 0.345.
, but we converted it to a decimal and got 0.345.
When adding decimals, the same rules are followed as when adding regular numbers. The addition of decimals is done by digits: tenths are added to tenths, hundredths to hundredths, and thousandths to thousandths.
Therefore, when adding decimals, the rule "point under the point" must be followed. The point under the point provides the very order in which the tenths add up to the tenths, the hundredths to the hundredths, and the thousandths to the thousandths.
Example 1. Find the value of the expression 1.5 + 3.4
Write the expression in columns, following the rule "point under the point":
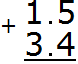
First add the fractional parts 5 + 4 = 9. Write the nine in the fractional part of our answer:
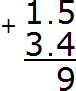
Now add the integers 1 + 3 = 4. Write the four in the whole part of our answer:

Now separate the whole part from the fractional part with a dot. To do this, again follow the rule "point under the point":
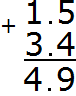
The answer is 4.9. So the value of the expression 1.5 + 3.4 is 4.9
1.5 + 3.4 = 4.9
Example 2. Find the value of the expression: 3.51 + 1.22
Write down the expression in columns, following the rule "point under the point".
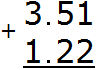
First, we add the fractional part, namely the hundredths part 1+2=3. Write the three in the hundredth part of our answer:
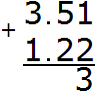
Now add the tenths of 5+2=7. Write the seven in the tenth of our answer:
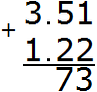
Now add the whole parts 3+1=4. Write the four in the whole part of our answer:
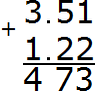
Separate the whole part from the fractional part with a dot, observing the rule "point under the point":
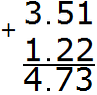
The answer is 4.73. So the value of the expression 3.51 + 1.22 is 4.73
3.51 + 1.22 = 4.73
As with regular numbers, adding decimals may cause a digit overflow. In this case, one digit is written in the answer, and the rest is transferred to the next digit.
Example 3. Find the value of the expression 2.65 + 3.27
Write the expression in columns:
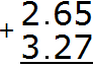
We add the hundredths of 5+7=12. The number 12 will not fit in the hundredth part of our answer. Therefore, write the number 2 in the hundredth part, and carry the one to the next digit:
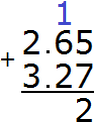
Now add the tenths of 6+2=8 plus the one we got from the previous operation, we get 9. Write the number 9 in the tenth part of our answer:
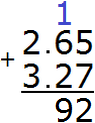
Now add the integers 2+3=5. Write the number 5 in the whole part of our answer:
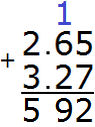
Separate the whole part from the fractional part with a dot:
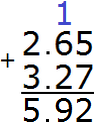
The answer is 5.92. So the value of the expression 2.65 + 3.27 is 5.92
2.65 + 3.27 = 5.92
Example 4. Find the value of the expression 9.5 + 2.8
Write the expression in the column
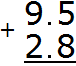
We add the fractional parts 5 + 8 = 13. The number 13 will not fit into the fractional part of our answer, so we write the number 3 first, and carry the one to the next digit, or rather, carry it to the whole part:
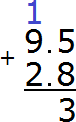
Now add the integers 9+2=11 plus the one we got from the previous operation, we get 12. Write the number 12 in the whole part of our answer:
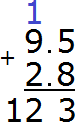
Separate the whole part from the fractional part with a dot:

The answer is 12.3. So the value of the expression 9.5 + 2.8 is 12.3
9.5 + 2.8 = 12.3
When adding decimals, the number of digits after the point in both fractions must be the same. If there are not enough digits, these places in the fractional part are filled with zeros.
Example 5. Find the value of the expression: 12.725 + 1.7
Before writing the expression in the column, make the number of digits after the decimal point in both fractions the same. The decimal 12.725 has three digits after the decimal point, while the fraction 1.7 has only one. So in the fraction 1.7, we need to add two zeros at the end. Then we have a fraction 1.700. Now we can write down the expression in columns and start calculating:
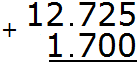
Add up the thousandths of 5+0=5. Write the number 5 in the thousandth part of our answer:
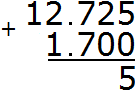
Add the hundredths of 2+0=2. Write the number 2 in the hundredth part of our answer:
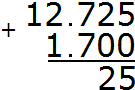
Add up the tenths 7+7=14. The number 14 will not fit in the tenth part of our answer. So we write the number 4 first, and carry the one to the next digit:
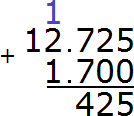
Now add the integers 12+1=13 plus the one we got from the previous operation, we get 14. Write the number 14 in the whole part of our answer:
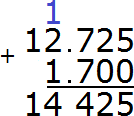
Separate the whole part from the fractional part with a dot:
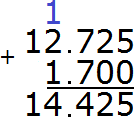
The answer is 14,425. So the value of the expression 12.725+1.700 is 14.425
12.725+ 1.700 = 14.425
Subtracting decimals
When subtracting decimals, you must follow the same rules as for addition: "point under the point" and "equal number of digits after the point".
Example 1. Find the value of the expression 2.5 - 2.2
Write the expression in columns, following the rule "point under the point":
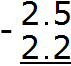
Calculate the fractional part 5-2=3. Write the number 3 in the tenth part of our answer:

Calculate the whole part 2-2=0. Write zero in the whole part of our answer:
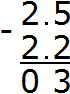
Separate the whole part from the fractional part with a dot:
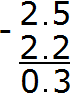
The answer is 0.3. So the value of the expression 2.5 - 2.2 is 0.3
2.5 − 2.2 = 0.3
Example 2. Find the value of the expression 7.353 - 3.1
The number of digits after the decimal point is different in the expression. There are three digits after the dot in fraction 7.353, and only one digit in fraction 3,1. So in the fraction 3.1, two zeros must be added at the end to make the number of digits in both fractions the same. Then we get 3.100.
Now we can write the expression in the column and calculate it:
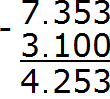
The answer is 4.253. So the value of the expression 7.353 - 3.1 is 4.253
7.353 — 3.1 = 4.253
As with regular numbers, sometimes you will have to borrow a unit from a neighboring digit if subtraction becomes impossible.
Example 3. Find the value of the expression 3.46 - 2.39
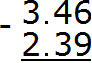
Subtract the hundredths of 6-9. You cannot subtract 9 from the number 6. So you need to take one from the next digit. By taking one from the next digit, number 6 turns into number 16. Now you can calculate the hundredths of 16-9=7. Write the seven in the hundredth part of our answer:
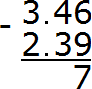
Now subtract the tenths. Since we took one unit in the tenths digit, the digit that was located there has decreased by one unit. In other words, the digit in the place of tenths is no longer 4, but 3. Let's calculate tenths 3-3=0. Write zero in the tenth part of our answer:
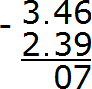
Now subtract the whole parts 3-2=1. Write one in the whole part of our answer:

Separate the whole part from the fractional part with a dot:
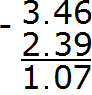
The answer is 1.07. So the value of the expression 3.46-2.39 is 1.07
3.46−2.39=1.07
Example 4. Find the value of the expression 3-1.2
In this example, a decimal is subtracted from a whole number. Write this expression in the column so that the whole part of the decimal 1.23 is under the number 3
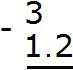
Now make the number of digits after the dot the same. To do this, put a dot after the number 3 and add a zero:
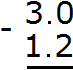
Now subtract the tenths: 0-2. The number 2 cannot be subtracted from zero. That is why we need to take one from the next digit. By taking one from the neighboring digit, 0 turns into 10. Now we can calculate the tenths of 10-2=8. Write the eight in the tenth part of our answer:

Now we subtract the integers. The whole used to be number 3, but we took one unit away from it. As a result, it turned into number 2. So we subtract 1 from 2. 2−1=1. Write one in the whole part of our answer:

Separate the whole part from the fractional part with a dot:
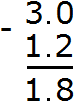
The answer is 1.8. So the value of the expression 3-1.2 is 1.8.
3 − 1.2 = 1.8
Multiplying decimals
Multiplying decimals is easy and even fun. To multiply decimals, you have to multiply them like regular numbers without paying attention to the dots.
When you get the answer, you must separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in both fractions, then count as many digits to the right in the answer and put a dot.
Example 1. Find the value of the expression 2.5 × 1.5
Multiply these decimals as regular numbers, ignoring the dots. To ignore the dots, you can pretend for a while that they do not exist at all:
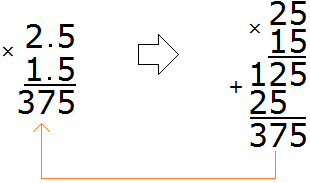
We got 375. In this number it is necessary to separate the whole part from the fractional part with a dot. To do that, count the number of digits after the point in fractions 2.5 and 1.5. The first fraction has one digit after the point, and the second fraction has one digit after the point. The total is two digits.
We return to the number 375 and start moving from right to left. We need to count two digits to the right and put a dot:
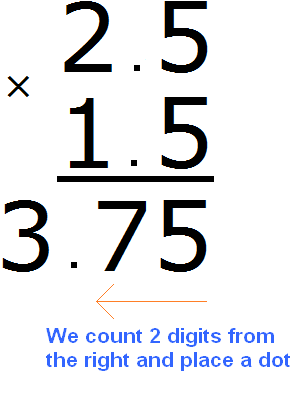
The answer is 3.75. So the value of the expression 2.5 × 1.5 is 3.75
2.5 × 1.5 = 3.75
Example 2. Find the value of the expression 12.85 × 2.7
Multiply these decimals without paying attention to the dots:

We got 34695. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in fractions 12.85 and 2.7. Fractions 12.85 have two digits after the dot, fractions 2.7 have one digit - three digits in total.
Go back to the number 34695 and start moving from right to left. We need to count three digits to the right and put a dot:

The answer is 34.695. So the value of the expression 12.85 × 2.7 is 34.695
12.85 × 2.7 = 34.695
Multiplying a decimal by a whole number
Sometimes situations arise where you want to multiply a decimal by a whole number.
To multiply a decimal and a whole number, you must multiply them without paying attention to the dot in the decimal. Once you have the answer, you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in the decimal, then count as many digits to the right in the answer and put a dot.
For example, multiply 2.54 by 2
Multiply the decimal 2.54 by the whole number 2, ignoring the dot:
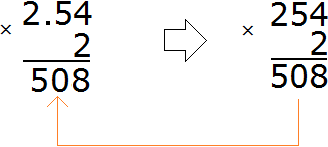
We got the number 508. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in the fraction 2.54. There are two digits after the dot in the fraction 2.54.
Go back to the number 508 and start moving from right to left. We need to count the two digits to the right and put a dot:

The answer is 5.08. So the value of the expression 2.54 × 2 is 5.08.
2.54 × 2 = 5.08
Multiplying of decimals by 10, 100, 1000
Multiplying decimals by 10, 100 or 1000 is done in the same way as multiplying decimals by regular numbers.
You must do the multiplication without paying attention to the dot in the decimal, then separate the whole part from the fractional part in the answer by counting off as many digits to the right as there were digits after the dot in the decimal.
For example, multiply 2.88 by 10
Multiply the decimal 2.88 by 10, ignoring the dot in the decimal:
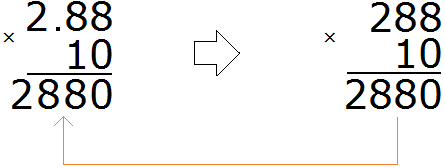
We got 2880. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in the fraction 2.88. We see that there are two digits after the dot in the fraction 2.88.
Go back to the number 2880 and start moving from right to left. We need to count the two digits to the right and put a dot:

The answer is 28.80. We discard the last zero and get 28.8. So the value of the expression 2.88×10 is 28.8
2.88 × 10 = 28.8
There is a second way to multiply decimals by 10, 100, 1000. This method is much easier and more convenient. It consists in moving the point in the decimal to the right by as many digits as there are zeros in the multiplier.
For example, solve the previous example 2.88×10 this way. Without giving any calculations, we immediately look at the multiplier 10. We are interested in how many zeros it contains. We see that it has one zero. Now in the fraction 2.88 move the point to the right by one digit, we get 28.8.
2.88 × 10 = 28.8
Let's try multiplying 2.88 by 100. Immediately we look at the multiplier 100. We are interested in how many zeros it contains. We see that it has two zeros. Now in the fraction 2.88 move the point to the right by two digits and we get 288
2.88 × 100 = 288
Let's try multiplying 2.88 by 1000. Immediately we look at the multiplier of 1000. We are interested in how many zeros it contains. We see that it has three zeros. Now in the fraction 2.88 we move the point to the right by three digits. The third digit is not there, so we add another zero. We end up with 2880.
2.88 × 1000 = 2880
Multiplying decimals by 0.1, 0.01 and 0.001
Multiplying decimals by 0.1, 0.01 and 0.001 is done in the same way as multiplying a decimal by a decimal.
It is necessary to multiply fractions like regular numbers and put a dot in the answer, counting as many digits to the right as there are digits after the dot in both fractions.
For example, multiply 3.25 by 0.1
Multiply these fractions like regular numbers, ignoring the dots:
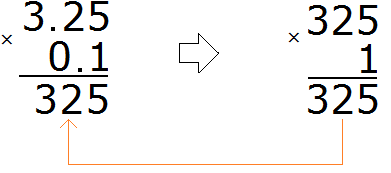
We got 325. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the point in fractions 3.25 and 0.1. There are two digits after the dot in fraction 3.25 and one digit in fraction 0.1. The total is three digits.
Go back to 325 and start moving from right to left. We need to count three digits to the right and put a dot. After counting the three digits, we find that the digits have run out. In this case we need to add one zero and put a dot:
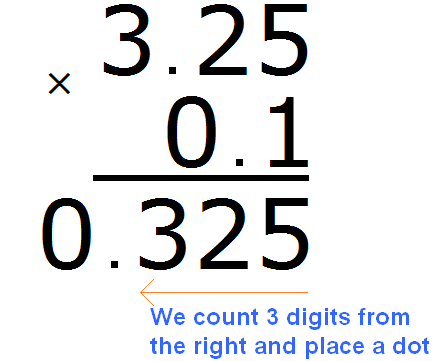
The answer is 0.325. So the value of the expression 3.25 × 0.1 is 0.325
3.25 × 0.1 = 0,325
There is a second way to multiply decimals by 0.1, 0.01 and 0.001. This method is much easier and more convenient. It consists in the fact that the point in the decimal is moved to the left by as many digits as zeros in the multiplier.
For example, solve the previous example 3.25 × 0.1 this way. Without giving any calculations, we immediately look at the multiplier 0.1. We are interested in how many zeros it contains. We see that it contains one zero. Now, in the fraction 3.25, move the decimal point to the left by one digit. Having moved the dot one digit to the left, we see that there are no more digits before the three. In this case, add one zero and put a dot. The result is 0.325
3.25 × 0.1 = 0,325
Let's try to multiply 3.25 by 0.01. Immediately we look at the multiplier 0.01. We are interested in how many zeros it contains. We see that it has two zeros. Now in the fraction 3.25 move the point to the left by two digits, we get 0.0325
3.25 × 0,01 = 0.0325
Let's try multiplying 3.25 by 0.001. Immediately we look at the multiplier 0.001. We are interested in how many zeros it contains. We see that it has three zeros. Now in the fraction 3.25 we move the point to the left by three digits, we get 0.00325
3.25 × 0.001 = 0.00325
Do not confuse multiplying decimals by 0.1, 0.001, and 0.001 with multiplying by 10, 100, and 1000. A typical mistake most people make.
When multiplying by 10, 100, 1000, the point is moved to the right by as many digits as there are zeros in the multiplier.
And when multiplying by 0.1, 0.01 and 0.001, the point is moved to the left as many digits as there are zeros in the multiplier.
If this is difficult to remember at first, you can use the first method, in which multiplication is done as with regular numbers. In the answer, you will need to separate the whole part from the fractional part by counting off as many digits to the right as there are digits after the point in both fractions.
Dividing a smaller number by a larger number. Advanced level.
In a previous lesson, we said that dividing a smaller number by a larger number produces a fraction with the numerator being the smaller-one and the denominator being the bigger-one.
For example, to divide one apple by two, you need to write 1 (one apple) in the numerator and 2 (two friends) in the denominator. The result is a fraction of ![]() . So each friend gets
. So each friend gets ![]() of an apple. In other words, half an apple. The fraction
of an apple. In other words, half an apple. The fraction ![]() is the answer to the problem "how to divide an apple between two people".
is the answer to the problem "how to divide an apple between two people".
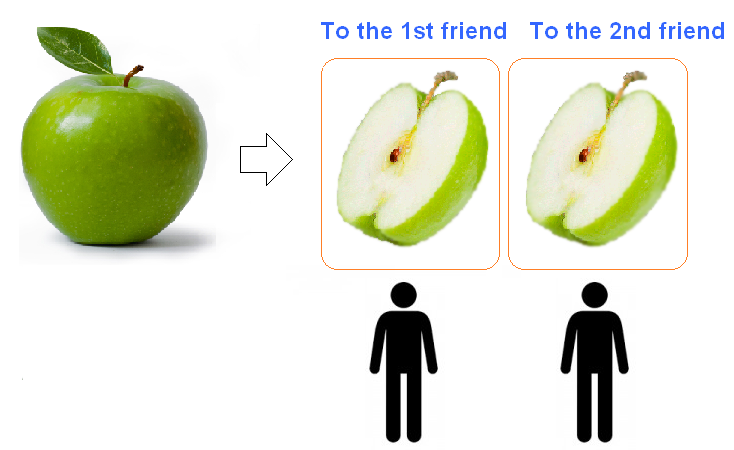
It turns out that you can solve this problem further by dividing 1 by 2. After all, the fractional line in any fraction means division, and therefore in fractions this division is allowed. But how? We are used to the fact that the dividend is always greater than the divisor. But here it is the opposite, the dividend is less than the divisor.
Everything becomes clear if you remember that fraction means partition, division And so a unit can be divided into as many parts as you want, not just two parts.
Dividing a smaller number by a larger number produces a decimal in which the whole part is 0 (zero). The fractional part can be anything.
So, divide 1 by 2. Solve this example with a long division (column division):
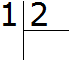
You can't just divide one by two by an whole. If you ask the question "how many twos are in one", the answer is 0. So we write 0 in the quotient and dot it:
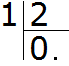
Now multiply the quotient by the divisor, as usual, to take out the remainder:
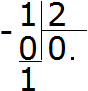
Now is the moment when the one can be divided into two parts. To do this, add another zero to the right of the resulting one:
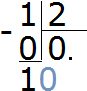
We got 10. We divide 10 by 2 and get 5. Write 5 on the fractional part of our answer:
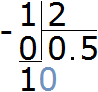
Now pull out the last remainder to complete the calculation. Multiply 5 by 2 to get 10
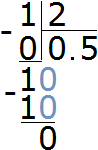
The answer is 0.5. So fraction ![]() equals 0.5
equals 0.5
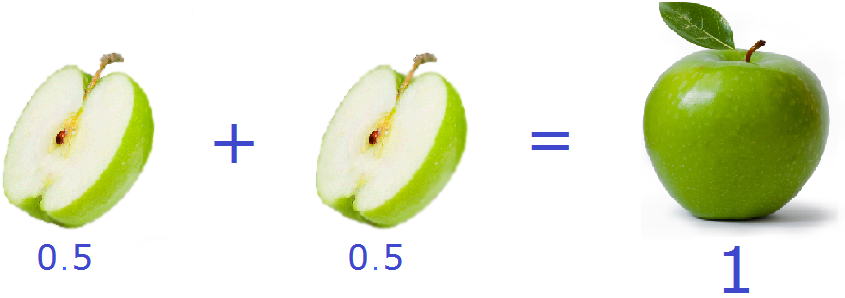
Half of an apple ![]() can also be written with the decimal 0.5. If we add the two halves (0.5 and 0.5), we again get the original one whole apple:
can also be written with the decimal 0.5. If we add the two halves (0.5 and 0.5), we again get the original one whole apple:

This point can also be understood by imagining how 1 cm is divided into two parts. If you divide 1 cm by 2 parts, you get 0.5 cm
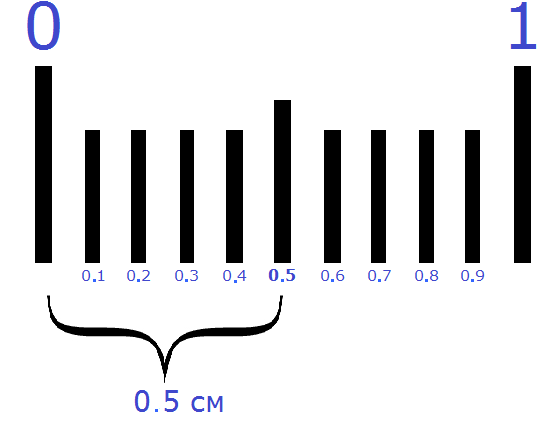
Example 2. Find the value of the expression 4 : 5
How many fives are in a four? None. Write 0 in the quotient and put a decimal point in it:
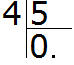
We multiply 0 by 5, we get 0. We write zero under the four. Immediately subtract that zero from the divisor:
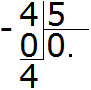
Now we begin to divide (divide) the four into 5 parts. To do this, add a zero to the right of 4 and divide 40 by 5 to make 8. Write the eight in the quotient.
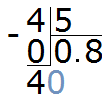
Complete the example by multiplying 8 by 5 to get 40:
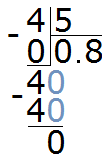
The answer is 0.8. So the value of the expression 4 : 5 is 0.8
Example 3. Find the value of the expression 5 : 125
How many numbers are 125 in five? None. Write 0 in the quotient and dot it:
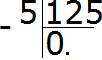
Multiply 0 by 125 to get 0. Write 0 under the five. Immediately subtract 0 from the five.
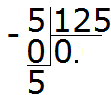
Now let's start splitting the five into 125 parts. To do this, write a zero on the right side of this five:
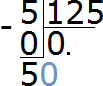
Divide 50 by 125. How many numbers are 125 in the number 50? None. So we again write 0 in the quotient.
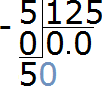
We multiply 0 by 125, we get 0. We write that zero under 50. Immediately subtract 0 from 50.
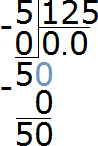
Now divide the number 50 into 125 parts. To do this, write another zero to the right of 50:
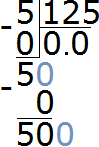
Divide 500 by 125. How many numbers 125 are in the number 500. There are four numbers 125 in the number 500. Write the four in the quotient:
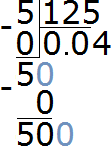
Complete the example by multiplying 4 by 125 to get 500
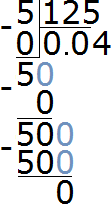
The answer is 0.04. So the value of the expression 5 : 125 is 0.04
Dividing numbers without a remainder
In the division lesson we learned how to divide numbers with a remainder. For example, to divide 9 by 5, we did the following:
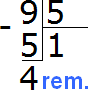
and went on to say that "nine divided by five would be one and four in the remainder".
Now we have the necessary knowledge to divide 9 by 5 without a remainder. Our task is to divide the remainder of 4 into 5 parts. In other words, divide a smaller number by a larger number.
So, let's put a dot after the one in the quotient, indicating that we have finished dividing the whole parts and are moving on to the fractional part:
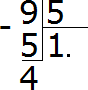
Add zero to the remainder of 4
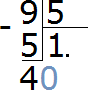
Now divide 40 by 5, and we get 8. Write the eight in the quotient:
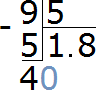
What to do next we already know. Take out the remainder (if any). Multiply the eight by the divisor 5, and write down the result under 40:
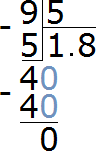
40−40=0. We got 0 in the remainder. This completes the division. Dividing 9 by 5 results in a decimal of 1.8:
9 : 5 = 1.8
Example 2. Divide 84 by 5 without a remainder
First divide 84 by 5 as usual with a remainder:
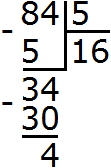
We got a total of 16 and another 4 in the remainder. Now divide this residue by 5. We put a dot in the quotient and add 0 to the remainder of 4.
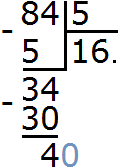
Now divide 40 by 5, and we get 8. Write the eight in the quotient after the point:
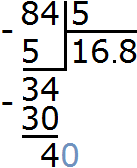
and finish the example by checking if there is still a remainder:
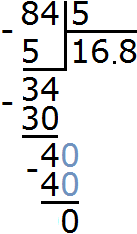
84 : 5 = 16.8
Dividing a decimal by a whole number
A decimal, as we know, consists of a whole part and a fractional part. When dividing a decimal by a whole number, the first thing to do is:
- divide the whole part of the decimal by this number;
- after the whole part is divided, you must immediately put a dot in the quotient and continue the calculation as in the usual division.
For example, divide 4.8 by 2
Let's write this example with a corner:
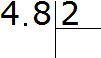
Now divide the whole part by two. Four divided by two is two. Write the two in the quotient and immediately put a dot:
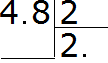
Now multiply the quotient by the divisor and see if there is a remainder of the division:
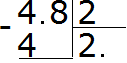
4−4=0. The remainder is zero. Zero is not written down yet, since the solution is not complete. Then continue to calculate, as in the usual division. Write down 8 and divide it by 2
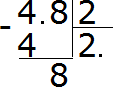
8 : 2 = 4. Write the four in the quotient and immediately multiply it by the divisor:
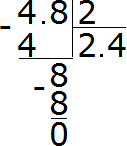
The answer is 2.4. The value of the expression 4.8 : 2 is 2.4
Example 2. Find the value of the expression 8.43 : 3
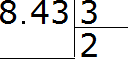
We divide 8 by 3 and get 2. Immediately put a dot after the two:
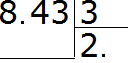
Now multiply the quotient by the divisor 2 × 3 = 6. Write the six under the eight and find the remainder:
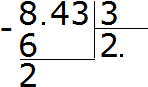
Then continue to calculate as in the usual division. Take off 4
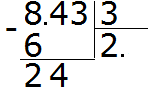
Divide 24 by 3, we get 8. Write the eight in the quotient. Immediately multiply it by the divisor to find the remainder of the division:
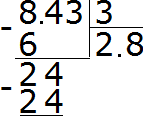
24−24=0. The remainder is zero. Zero is not written down yet. Take the last 3 from the divisor and divide by 3, we get 1. Immediately multiply 1 by 3 to complete this example:
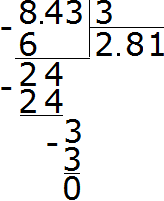
The answer is 2.81. So the value of the expression 8.43 : 3 is 2.81
Dividing a decimal by a decimal
To divide a decimal by a decimal, you must move the dot to the right in the dividend and in the divisor to the same number of digits as there are after the dot in the dividend, and then divide by a regular number.
For example, divide 5.95 by 1.7
Write this expression in the corner
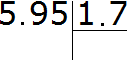
Now move the dot to the right in the divident and in the divisor to the same number of digits as there are after the point in the divisor. There is one digit after the dot in the divisor. So we must move the point to the right by one digit in the dividend and divisor. Let's move it:
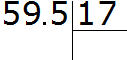
After moving the point to the right by one digit, the decimal 5.95 became 59.5. And the decimal 1.7, after moving the point to the right by one digit, turned into the regular number 17. And we already know how to divide a decimal by a regular number. Further calculation is not very difficult:
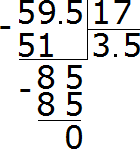
The point is moved to the right in order to facilitate division. This is allowed because when you multiply or dividend a divisor and a divisor by the same number, the quotient does not change. What does this mean?
This is one of the interesting features of division. It is called the property of the quotient. Consider the expression 9 : 3 = 3. If in this expression the divisor and the divisor are multiplied or divided by the same number, the quotient 3 will not change.
Let's multiply the divisor and the divisor by 2, and see what happens:
(9 × 2) : (3 × 2) = 18 : 6 = 3
As you can see from the example, the quotient does not change.
The same thing happens when we move the point in the dividend and divisor. In the previous example, where we divided 5.91 by 1.7, we moved the point one digit to the right in the dividend and divisor. After moving the point, the 5.91 was converted to 59.1, and the 1.7 was converted to 17. What was really happening here was multiplying by 10. This is what it looked like:
5.91 × 10 = 59.1
1,7 × 10 = 17
Therefore, the number of digits after the dot in the dividend determines by how many digits the dividend and divisor will be multiplied. In other words, the number of digits after the dot in the dividend will determine by how many digits in the dividend and in the divisor the dot will be moved to the right.
Dividing a decimal by 10, 100, 1000
Dividing a decimal by 10, 100, or 1000 is done in the same way as dividing a decimal by a whole number. For example, divide 2.1 by 10. Solve this example with a column division:
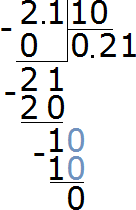
But there is a second way. It is easier. The essence of this method is that the point in the divisor is moved to the left by as many digits as there are zeros in the divisor.
Let's solve the previous example this way. 2,1 : 10. We look at the divisor. We are interested in how many zeroes are in it. We see that there is one zero. It means that in the divisor 2.1 we need to move the point to the left by one digit. We move the point to the left by one digit and see that there are no more digits left. In this case, we add another zero before the digit. As a result, we get 0.21
2.1 : 10 = 0.21
Let's try to divide 2.1 by 100. The number 100 has two zeros. So in the divisible 2.1 we have to move the point to the left by two digits:
2.1 : 100 = 0.021
Let's try to divide 2.1 by 1000. There are three zeros in the number 1000. So in the divisible 2.1 we have to move the point to the left by three digits:
2.1 : 1000 = 0.0021
Dividing a decimal by 0.1, 0.01, and 0.001
Dividing a decimal by 0.1, 0.01, and 0.001 is done in the same way as dividing a decimal by a decimal. In the dividend and in the divisor you must move the point to the right by as many digits as there are after the point in the divisor.
For example, divide 6.3 by 0.1. First, move the dots in the dividend and divisor to the right by as many digits as there are after the dot in the divisor. There is one digit after the point in the dividend. So we move the points in the dividend and divisor to the right by one digit.
After moving the point to the right by one digit, the decimal 6.3 turns into the regular number 63, and the decimal 0.1 turns into a unit after moving the point to the right by one digit. And dividing 63 by 1 is very simple:
63 : 1 = 63
So the value of the expression 6.3 : 0.1 is 63
6.3 : 0.1 = 63
But there is a second way. It is easier. The essence of this method is that the point in the dividend is moved to the right by as many digits as there are zeros in the divisor.
Let's solve the previous example this way. 6,3 : 0,1. We look at the dividend. We are interested in how many zeroes are in it. We see that there is one zero. It means that in the dividend 6.3 we need to move the point to the right by one digit. We move the point to the right by one digit and get 63
6,3 : 0.1 = 63
Let's try to divide 6.3 by 0.01. There are two zeros in the divisor 0.01. So in the divisor 6.3 we need to move the point to the right by two digits. But the divisor has only one digit after the point. In this case, add another zero at the end. The result will be 630
6,3 : 0.01 = 630
Let's try to divide 6.3 by 0.001. There are three zeros in the divisor 0.001. So in the dividend 6.3 we have to move the point to the right by three digits:
6,3 : 0.001 = 6300
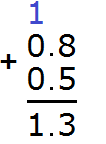
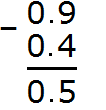
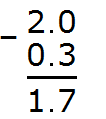
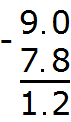
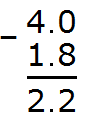
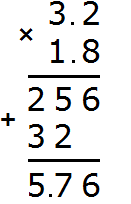
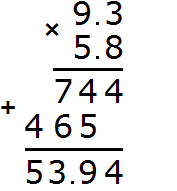
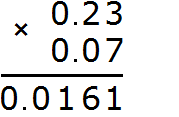
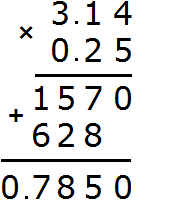
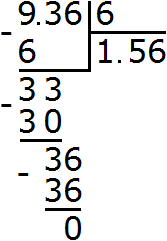
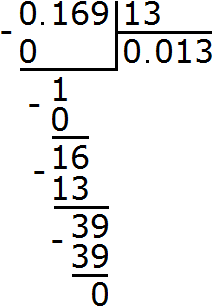
Comments