Decomposing a polynomial into factors means representing it as a product of two or more polynomials.
An example of a factorization of a polynomial is putting the common factor out of brackets, because the original polynomial is the product of two factors, one of which is a monomial and the other a polynomial.
Decomposition by putting the common factor out of brackets
Putting the common factor outside the brackets creates a product of two factors, one of which is a monominal and the other a polynominal. For example:
6x + 3xy = 3x(2 + y)
When studying polynomials, a monomial is usually considered a polynomial consisting of one term. Therefore, when a common multiplier in a polynomial is taken out of brackets, the original polynomial is said to be represented as a product of polynomials.
In our example, the polynomial 6x + 3xy was represented as the product of polynomials 3x and (2 + y). Alternatively, the polynomial 6x + 3xy is said to be decomposed into the factors 3x and (2 + y)
There are also polynomials in which you can put a common multiplier, which is a binomial, outside the brackets. For example, consider the polynomial 5a(x + y) + 7a(x + y). In this polynomial, the common factor is a binomial (x + y). Take it out of brackets:
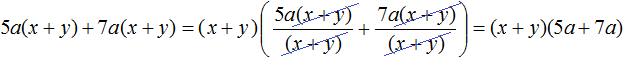
Decomposition by grouping method
Some polynomials contain a group of terms that have a common multiplier. Such groups can be bracketed and then the common multiplier can be taken out of these brackets. The result is a decomposition of the original polynomial into multipliers, which is called decomposition by the grouping method.
Consider the following polynomial:
ax + ay + 3x + 3y
The terms ax and ay have a common factor a. Write out these terms and put them in brackets:
(ax + ay)
Then in the polynomial ax + ay + 3x + 3y the terms 3x and 3y have a common factor 3. Write out these terms and also put them in brackets:
(3x + 3y)
Now connect the expressions (ax + ay) and (3x + 3y) with a plus sign
(ax + ay) + (3x + 3y)
In the polynomial (ax + ay), bracket the common factor a, and in the polynomial (3x + 3y) bracket the common factor 3. This should be done in the original expression:
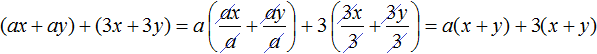
Then we notice that the binomial (x + y) is a common multiplier. Take it out of brackets. Continue solving in the original example. The result is:

Let us write down the solution shorter, without describing in detail how each term was divided by a common multiplier. Then the solution will be more compact:
![]()
To check if we have correctly decomposed the polynomial into multipliers, multiply (x + y)(a + 3). If we have done it correctly, we get the polynomial ax + ay + 3x + 3y
(x + y)(a + 3) = ax + ay + 3x + 3y
Example 2. Decompose a polynomial 9x + ax - 9y - ay into factors by grouping.
The terms 9x and -9y have a common factor 9. And the terms ax and -ay have a common factor a. Let us group them using brackets, and combine them with a plus sign
(9x − 9y) + (ax − ay)
In the first group (9x - 9y), bracket the common factor 9. In the second group (ax - ay), bracket the common factor a
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y)
Next, put the binomial (x - y) behind the parentheses
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y) = (x − y)(9 + a)
Example 3. Decompose polynomial ab - 3b + b2 - 3a into multipliers by grouping.
Group the first term ab with the fourth term -3a. And group the second term -3b with the third term b2. Don't forget that the groups should be grouped with a plus sign
(ab − 3a) + (−3b + b2)
In the first group, put the common factor a behind the brackets, and in the second group, the common factor b
(ab − 3a) + (−3b + b2) = a(b − 3) + b(−3 + b)
In the second product b(-3 + b) change the order of the terms in the (-3 + b) factor. Then we obtain b(b - 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3)
Now put the common factor (b - 3) behind the brackets.
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3) = (b − 3)(a + b)
Example 4. Decompose the polynomial x2y + x + xy2 + y + 2xy + 2 into factors by grouping.
Let's group the first member of the polynomial with the second, the third with the fourth, and the fifth with the sixth:
![]()
In the first group, put the common factor x behind the brackets, in the second group, the common factor y, and in the third group, the common factor 2.
![]()
Then we see that the polynomial (xy + 1) is a common factor. Take it out of brackets:
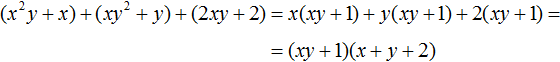
Decomposition by the formula for the square of the sum of two expressions
The reduced multiplication formulas we looked at in the last lesson can be applied to the decomposition of polynomials into multipliers.
Recall what the formula for the square of the sum of two expressions looks like:
(a + b)2 = a2 + 2ab + b2
Let's swap the left and the right parts, and we get:
a2 + 2ab + b2 = (a + b)2
The left part of this equality is a polynomial, and the right part is the product of polynomials, because the expression (a + b)2 is a multiplication of two factors, each equal to a polynomial (a + b).
Therefore, if we find an expression of the form a2 + 2ab + b2, we can represent it as (a + b)(a + b). In other words, decompose it into (a + b) and (a + b).
a2 + 2ab + b2 = (a + b)(a + b)
Example 1. Decompose a polynomial 4x2 + 12xy + 9y2
To use the formula a2 + 2ab + b2 = (a + b)2, you need to know what the variable a equals in this case and what the variable b equals.
The first term of the polynomial 4x2 + 12xy + 9y2 is the result of squaring the monomial 2x, since (2x)2 = 4x2. The third term 9y2 is the result of squaring the monomial 3y because (3y)2 = 9y2, and the term 12xy is the doubled product of terms 2x and 3y, that is 2 × 2x × 3y = 12xy.
Obviously, the variable a in this case is 2x, and the variable b is 3y
a = 2x
b = 3y
Then we can conclude that once the expression 4x2 + 12xy + 9y2 looked like the sum square (2x + 3y)2, but as a result of applying the sum square formula it turned into a polynomial 4x2 + 12xy + 9y2. Our task is to return it to its former form, that is, to represent it as (2x + 3y)2
4x2 + 12xy + 9y2 = (2x + 3y)2
And since (2x + 3y)2 is the product of two factors each equal to a polynomial (2x + 3y), the initial polynomial 4x2 + 12xy + 9y2 can be represented as a factorization of (2x + 3y) and (2x + 3y)
4x2 + 12xy + 9y2 = (2x + 3y)(2x + 3y)
The full solution can be written as follows:
4x2 + 12xy + 9y2 = (2x)2 + 2 × 2x × 3y + (3y)2 = (2x + 3y)2 = (2x + 3y)(2x + 3y)
Example 2. Decompose a polynomial x2 + 12x + 36
The first term of this polynomial is the result of squaring a monomial x, because x2 = x2, the third term is the result of squaring 6, because 62 = 36, and the term 12x is the doubling of x and 6, because 2 × x × 6 = 12x.
Use the formula a2 + 2ab + b2 = (a + b)2. The variable a is the monomial of x, and the variable b is the monomial of 6. Hence:
x2 + 12x + 36 = (x + 6)2
And since (x + 6)2 is the product of two factors each equal to a polynomial (x + 6), the original polynomial x2 + 12x + 36 can be represented as a factorization of (x + 6) and (x + 6)
x2 + 12x + 36 = (x + 6)(x + 6)
Decomposition by the formula for the square of the difference of two expressions
Like the formula for squaring the sum of two expressions, a polynomial can be decomposed into factors using the formula for squaring the difference of two expressions.
The formula for the square of the difference of two expressions looks like this:
(a − b)2 = a2 − 2ab + b2
If we swap the left and right parts of this formula, we get:
a2 − 2ab + b2 = (a − b)2
Since the right part is the product of two factors each equal to (a - b), a polynomial of the form a2 − 2ab + b2 can be decomposed into (a - b) and (a - b) multipliers.
a2 − 2ab + b2 = (a − b)(a − b)
Example 1. Decompose a polynomial 9x2 − 12xy + 4y2
To use the formula a2 − 2ab + b2 = (a − b)2, you need to know what the variable a equals in this case and what the variable b equals.
The first term of this polynomial is the result of squaring the monomial 3x, since (3x)2 = 9x2. The third term 4y2 is the result of squaring a monomial 2y because (2y)2 = 4y2, and the term 12xy is the doubled product of terms 3x and 2y, that is 2 × 3x × 2y = 12xy.
Obviously, the variable a in this case is 3x, and the variable b is 2y
a = 3x
b = 2y
Then we can conclude that 9x2 − 12xy + 4y2 once looked like the square of difference (3x − 2y)2, but by applying the squared difference formula it turned into the polynomial 9x2 − 12xy + 4y2. Our task is to return it to its former form, i.e. to represent it as (3x − 2y)2
9x2 − 12xy + 4y2 = (3x − 2y)2
Since (3x - 2y)2 is the product of two factors each equal to a polynomial (3x - 2y), the initial polynomial 9x2 − 12xy + 4y2 can be represented as a factorization of (3x - 2y) and (3x - 2y)
9x2 − 12xy + 4y2 = (3x − 2y)(3x − 2y)
The full solution can be written as follows:
9x2 − 12xy + 4y2 = (3x)2 − 2 × 3x × 2y + (2y)2 = (3x − 2y)2 = (3x − 2y)(3x − 2y)
Example 2. Decompose a polynomial x2 − 4x + 4
Use the formula for the square of the difference of two expressions:
x2 − 4x + 4 = x2 − 2 × x × 2 + 22 = (x − 2)2 = (x − 2)(x − 2)
Decomposition by the cube formula of the sum of two expressions
Recall what the formula for the cube of the sum of two expressions looks like:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Let's swap the left and the right parts, and we get:
a3 + 3a2b + 3ab2 + b3 = (a + b)3
The left part of this equality is a polynomial, and the right part is the product of polynomials, because the expression (a + b)3 is a multiplication of three factors, each equal to a polynomial (a + b).
Therefore, if we find an expression of the form a3 + 3a2b +3ab2 + b3, we can represent it as (a + b)(a + b)(a + b). That is, decompose it into (a + b), (a + b), and (a + b).
a3 + 3a2b + 3ab2 + b3 = (a + b)(a + b)(a + b)
Example 1. Decompose a polynomial m3 + 6m2n + 12mn2 + 8n3
Before applying the sum cube formula, we should analyze the given polynomial. Namely, make sure that we are really looking at the cube of the sum of two expressions.
To make sure that the original expression is the cube of the sum of two expressions, find out what variable a is equal in this case and what variable b is equal to.
The first term of this polynomial is the result of the cube of the monomial m
m3 = m3
The last term 8n3 is the result of the cube of the monomial 2n
(2n)3 = 8n3
The second term 6m2n is the tripled product of the square of the first expression m and the last 2n
3 × m2 × 2n = 6m2n
The third term 12mn2 is the tripled product of the first expression m and the square of the last expression 2n
3 × m × (2n)2 = 3 × m × 4n2 = 12mn2
That is, the initial polynomial m3 + 6m2n + 12mn2 + 8n3 corresponds to the cube of the sum of two expressions. The variable a in this polynomial corresponds to m, and the variable b corresponds to 2n
a = m
b = 2n
Then we can conclude that the expression m3 + 6m2n + 12mn2 + 8n3 once looked like the sum cube (m + 2n)3, but as a result of applying the sum cube formula, it turned into a polynomial m3 + 6m2n + 12mn2 + 8n3. Our task is to return it to its former form, i.e. to represent it as (m + 2n)3
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)3
And since (m + 2n)3 is the product of three factors, each equal to a polynomial (m + 2n), the initial polynomial m3 + 6m2n + 12mn2 + 8n3 can be represented as a factorization of (m + 2n), (m + 2n) and (m + 2n)
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)(m + 2n)(m + 2n)
Example 2. Decompose a polynomial 125x3 + 75x2 + 15x + 1
The first term of this polynomial is the result of the cube of the monomial 5x
(5x)3 = 125x3
The last term 1 is the result of the cube of the monomial 1
13 = 1
The second term 75x2 is the tripled product of the square of the first expression 5x and the last one 1
3 × (5x)2 × 1 = 3 × 25x2 = 75x2
The third term 15x is the tripled product of the first expression 5x and the square of the second expression 1
3 × 5x × 12 = 15x
Let's use the formula a3 + 3a2b + 3ab2 + b3 = (a + b)3. The variable a is the single term 5x, and the variable b is the single term 1
a = 5x
b = 1
Therefore,
125x3 + 75x2 + 15x + 1 = (5x + 1)3
Since (5x + 1)3 is the product of three factors each equal to a polynomial (5x + 1), the original polynomial 125x3 + 75x2 + 15x + 1 can be represented as a factorization of (5x + 1), (5x + 1), and (5x + 1)
125x3 + 75x2 + 15x + 1 = (5x + 1)(5x + 1)(5x + 1)
Decomposition by the cube formula of the difference of two expression
Like the formula for the cube of the sum of two expressions, a polynomial can be decomposed into factors using the formula for the cube of the difference of two expressions.
Recall what the formula for the cube of the difference of two expressions looks like:
(a − b)3 = a3 − 3a2b + 3ab2 − b3
If we swap the left and right parts of this formula, we get:
a3 − 3a2b + 3ab2 − b3 = (a − b)3
Since the right-hand side is the product of three factors each equal to (a - b), a polynomial of the form a3 − 3a2b + 3ab2 − b3 can be decomposed into (a - b), (a - b) and (a - b) multipliers.
a3 − 3a2b + 3ab2 − b3 = (a − b)(a − b)(a − b)
Example 1. Decompose a polynomial 64 − 96x + 48x2 − 8x3
Before applying the cube of difference formula, we should analyze the given polynomial. Namely, make sure that we are really looking at the cube of the difference of two expressions.
To make sure that the original expression is the cube of the difference of two expressions, find out what in this case the variable a is equal to and what the variable b is equal to.
The first term of this polynomial is the result of the cube of the monomial 4
43 = 64
The last term 8x3 is the result of the cube of the monomial 2x
(2x)3 = 8x3
The second term 96x is the tripled product of the square of the first expression 4 and the last expression 2x
3 × 42 × 2x = 3 × 16 × 2x = 96x
The third term 48x2 is the triple product of the first expression 4 and the square of the second expression 2x
3 × 4 × (2x)2 = 3 × 4 × 4x2 = 48x2
We see that the initial polynomial 64 − 96x + 48x2 − 8x3 corresponds to the cube of the difference of two expressions. The variable a in this polynomial corresponds to 4, and the variable b corresponds to 2x
a = 4
b = 2x
Then we can conclude that the expression 64 − 96x + 48x2 − 8x3 once looked like a cube of difference (4 − 2x)3, but as a result of applying the formula for the cube of difference it turned into a polynomial 64 − 96x + 48x2 − 8x3. Our task is to return it to its former form, that is, to represent it as (4 − 2x)3
64 − 96x + 48x2 − 8x3 = (4 − 2x)3
And since (4 - 2x)3 is the product of three factors, each of which is equal to (4 - 2x), the initial polynomial 64 − 96x + 48x2 − 8x3 can be represented as a factorization of (4 - 2x), (4 - 2x) and (4 - 2x)
64 − 96x + 48x2 − 8x3 = (4 − 2x)(4 − 2x)(4 − 2x)
Example 2. Decompose a polynomial 27 − 135x + 225x2 − 125x3
The first term of this polynomial is the result of the cube of the monomial 3
33 = 27
The last term 125 is the result of the cube of the monomial 5x
(5x)3 = 125x3
The second term 135x is the tripled product of the square of the first expression 3 and the last term 5x
3 × 32 × 5x = 3 × 9 × 5x = 135x
The third term 225x2 is the tripled product of the first expression 3 and the square of the second expression 5x
3 × 3 × (5x)2 = 3 × 3 × 25x2 = 225x2
Let's use the formula a3 − 3a2b + 3ab2 − b3 = (a − b)3. Where a is the monomial 3 and b is the monomial 5x
a = 3
b = 5x
Therefore,
27 − 135x + 225x2 − 125x3 = (3 − 5x)3
Since (3 − 5x)3 is the product of three factors each equal to a polynomial (3 - 5x), the initial polynomial 27 − 135x + 225x2 − 125x3 can be represented as a factorization of (3 - 5x), (3 - 5x) and (3 - 5x)
125x3 + 75x2 + 15x + 1 = (3 − 5x)(3 − 5x)(3 − 5x)
Decomposition by the formula for the difference of squares of two expressions
Recall what the formula for multiplying the difference of two expressions by their sum looks like:
(a − b)(a + b) = a2 − b2
If we swap the left and right parts of this formula, we get:
a2 − b2 = (a − b)(a + b)
This formula is called the difference of squares. It allows you to decompose an expression of the form a2 - b2 into (a - b) and (a + b) multiples.
Example 1. Decompose a polynomial 16x2 − 25y2
To use the formula a2 − b2 = (a − b)(a + b), find out what the variable a equals in this case and what the variable b equals.
The first term 16x2 is the result of the squaring of the monomial 4x
(4x)2 = 16x2
The second term 25y2 is the result of the squaring of the monomial 5y
(5y)2 = 25y2
That is, in this case the variable a corresponds to the monomial 4x, and the variable b corresponds to the monomial 5y
a = 4x
b = 5y
Now we can use the formula a2 − b2 = (a − b)(a + b). Let's substitute our values of a and b into it
(4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
The full solution can be written as follows:
16x2 − 25y2 = (4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
To check, we can multiply (4x - 5y)(4x + 5y). If we did it right, we should get 16x2 − 25y2
(4x − 5y)(4x + 5y) = 16x2 − 20xy + 20xy − 25y2 = 16x2 − 25y2
Example 2. Decompose a polynomial x2 − y2
In this case, the variable a corresponds to x, and the variable b corresponds to y. Then by the squared difference formula we have:
x2 − y2 = (x − y)(x + y)
The case as in this example is the simplest, because here you can immediately see what a equals and what b equals.
Most often, the terms that make up the initial difference are the results of the second power of some monomials. To find out what a and b are equal in this case, we need, as in the first example, to represent the terms of the original difference in the form of monomials squared.
For example, to decompose a polynomial 4x4 − 9y6 into multipliers, the initial terms must be presented in the form of the squared terms. The first term in the form of a squared monomial can be written as (2x2)2, because the calculation of this expression results in 4x4
(2x2)2 = 4x4
And the term 9y6 as a monomial squared can be written as (3y3)2, since calculating this expression results in 9y6
(3y3)2 = 9y6
Now we know what a and b are equal to. They are equal to 2x2 and 3y3, respectively. Let's substitute them into the formula a2 − b2 = (a − b)(a + b)
(2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
The full solution can be written as follows:
4x4 − 9y6 = (2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Despite the simplicity of decomposition using the difference-of-squares formula, frequent errors occur in these very tasks. To make sure that the task is solved correctly, it does not hurt to perform multiplication in the resulting decomposition. If the task is solved correctly, you should get the original polynomial.
Let's check this example by multiplication. We should have a polynomial 4x4 − 9y6
(2x2 − 3y3)(2x2 + 3y3) = 2x2(2x2 + 3y3) − 3y3(2x2 + 3y3)
= 4x4 + 6x2y3 − 6x2y3 − 9y6 = 4x4 − 9y6
Example 3. Decompose a polynomial 81 − 64
Let us represent the terms of the original difference in the form of monomials squared. Then we use the formula for the difference of squares:
81 − 64 = 92 − 82 = (9 − 8)(9 + 8)
Decomposition by the formula for the sum of the cubes of two expressions
We remember that the product of the sum of two expressions and the incomplete square of their difference equals the sum of the cubes of those expressions:
(a + b)(a2 − ab + b2) = a3 + b3
If we swap the left and the right parts of this formula, we get a formula called the sum of the cubes of two expressions:
a3 + b3 = (a + b)(a2 − ab + b2)
This formula allows you to decompose an expression of the form a3 + b3 into (a + b) and (a2 − ab + b2) multipliers.
Example 1. Decompose a polynomial 27x3 + 64y3
Let us represent the terms 27x3 and 64y3 as a monomials raised to a cube
27x3 + 64y3 = (3x)3 + (4y)3
Now let us use the formula for the sum of the cubes. The variable a in this case is 3x, the variable b is 4y
27x3 + 64y3 = (3x)3 + (4y)3 = (3x + 4y)((3x)2 − 3x × 4y + (4y)2) =
(3x + 4y)(9x2 − 12xy + 16y2)
Example 2. Decompose a polynomial 125 + 8
Let us represent the terms 125 and 8 as monomials raised to a cube:
125 + 8 = 53 + 23
Next, we use the formula for the sum of the cubes:
125 + 8 = 53 + 23 = (5 + 2)(25 − 10 + 4)
Decomposition by the formula for the difference of the cubes of two expressions
The product of the difference of two expressions and the incomplete square of their sum equals the difference of the cubes of these expressions:
(a − b)(a2 + ab + b2) = a3 − b3
If we swap the left and the right parts of this formula, we get a formula called the difference of the cubes of two expressions:
a3 − b3 = (a − b)(a2 + ab + b2)
This formula allows you to decompose an expression of the form a3 − b3 into (a - b) and (a2 + ab + b2) multipliers.
Example 1. Decompose a polynomial 64x3 − 27y3
Let us represent the terms 64x3 and 27y3 as a monomials raised to a cube:
64x3 − 27y3 = (4x)3 − (3y)3
Now let us use the formula for the difference of cubes. The variable a in this case equals 4x, the variable b equals 3y
64x3 − 27y3 = (4x)3 − (3y)3 = (4x − 3y)((4x)2 + 4x × 3y + (3y)2) =
(4x − 3y)(16x2 + 12xy + 9y2)
Example 2. Decompose a polynomial 64 − 27
Let us represent the terms 64 and 27 as monomials raised to a cube:
64 − 27 = 43 − 33 = (4 − 3)(16 + 12 + 9)
Example 3. Decompose a polynomial 125x3 − 1
Let us represent the terms 125x3 and 1 as monomials raised to a cube:
125x3 − 1 = (5x)3 − 13
Now let us use the formula for the difference of cubes. The variable a in this case equals 5x, the variable b equals 1
125x3 − 1 = (5x)3 − 13 = (5x − 1)((5x)2 + 5x × 1 + 12) =
(5x − 1)(25x2 + 5x + 1)
Decomposition in different ways
For some polynomials, you can apply different ways of decomposition to multipliers. For example, you can apply the bracketing method to one polynomial and then use one of the reduced multiplication formulas.
Example 1. Decompose a polynomial ax2 − ay2
This polynomial contains a common factor a. Take it out of the brackets:
ax2 − ay2 = a(x2 − y2)
The brackets form a polynomial, which is the difference of squares. Applying the formula for difference of squares. Then we obtain:
ax2 − ay2 = a(x2 − y2) = a(x − y)(x + y)
Example 2. Decompose a polynomial 3x2 + 6xy + 3y2
We put the common multiplier 3 out of the brackets.
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2)
The brackets form a polynomial which is the square of the sum of two expressions, namely expressions x and y. Then this sum square can be represented as (x + y)2 and then written as two factors, each of which is equal to (x + y)
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2) = 3(x + y)2 = 3(x + y)(x + y)
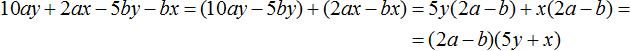
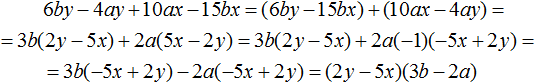
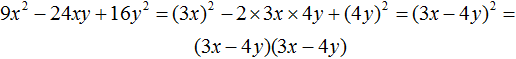
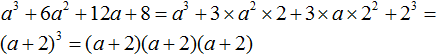
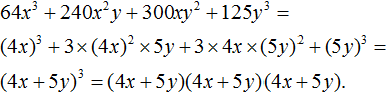
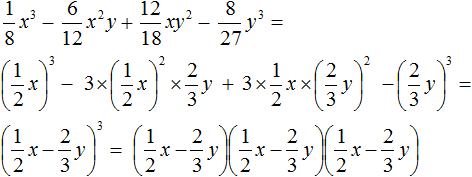
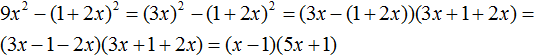
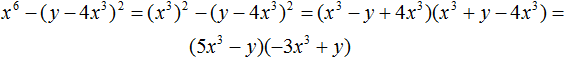
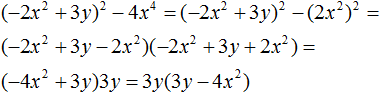
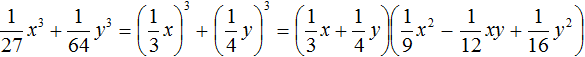
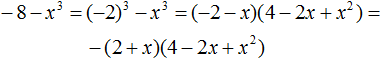
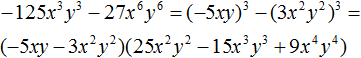
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.