Linear equations with two variables
John has $200 to eat lunch. A cake costs $25, and a cup of coffee costs $10. How many cakes and cups of coffee can he buy with $200?
Denote the number of cakes by x, and the number of cups of coffee by y. Then the cost of the cakes will be denoted by 25x, and the cost of the cups of coffee by 10y.
25x - is the cost of x cakes
10y - cost of y cups of coffee
The total should equal $200. Then you get an equation with two variables x and y
25x + 10y = 200
How many roots does this equation have?
It all depends on John's appetite. If he buys 6 cakes and 5 cups of coffee, the roots of the equation are 6 and 5.
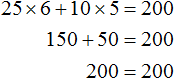
The pair of values 6 and 5 are said to be the roots of the equation 25x + 10y = 200. It is written as (6; 5), with the first number being the value of the x variable and the second being the value of the y variable.
6 and 5 are not the only roots that turn the equation 25x + 10y = 200 into an identity. For the same $200, a student can buy 4 cakes and 10 cups of coffee:
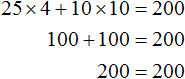
In this case, the roots of the equation 25x + 10y = 200 are a pair of values (4; 10).
Moreover, the student may not buy coffee at all, but buy cakes for all $200. Then the roots of the equation 25x + 10y = 200 will be the values 8 and 0
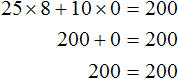
Or vice versa, don't buy cakes, but buy coffee for all $200. Then the roots of the equation 25x + 10y = 200 are 0 and 20
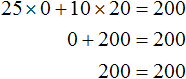
Try to list all possible roots of the equation 25x + 10y = 200. Assume that the values of x and y belong to the set of integers. And let these values be large or equal to zero:
x ∈ Z, y ∈ Z;
x ≥ 0, y ≥ 0
It would be more convenient for the student himself. It is more convenient to buy whole cakes than, for example, several whole cakes and half a cake. It is also more convenient to buy coffee in whole cups than, for example, several whole cups and half a cup.
Note that if x is odd, it is impossible to achieve equality with any y. Then the values of x are 0, 2, 4, 6, 8. Knowing x you can easily determine y
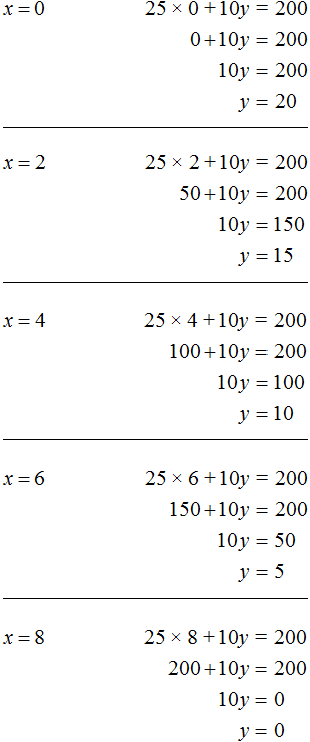
Thus, we obtained the following pairs of values (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). These pairs are solutions or roots of the equation 25x + 10y = 200. They convert this equation to an identity.
An equation of the form ax + by = c is called a linear equation with two variables. The solution or roots of this equation are the pair of values (x; y) that turns it into an identity.
Note also that if a linear equation with two variables is written in the form ax + by = c, then it is said to be written in the canonical (normal) form.
Some linear equations with two variables can be reduced to the canonical form.
For example, the equation 2(16x + 3y - 4) = 2(12 + 8x - y) can be reduced to the form ax + by = c. Open brackets in both parts of this equation, we obtain 32x + 6y - 8 = 24 + 16x - 2y. Group the summands containing unknowns on the left side of the equation and the summands free of unknowns on the right side. Then we obtain 32x - 16x + 6y + 2y = 24 + 8. Given like terms in both parts, we obtain the equation 16x + 8y = 32. This equation is reduced to the form ax + by = c and is canonical.
The equation 25x + 10y = 200 considered earlier is also a linear equation with two variables in canonical form. In this equation, the parameters a, b, and c are 25, 10, and 200, respectively.
In fact, the equation ax + by = c has countless solutions. In solving the equation 25x + 10y = 200, we looked for its roots only on the set of integers. As a result, we obtained several pairs of values that converted the equation to an identity. But on a set of rational numbers, the equation 25x + 10y = 200 would have innumerable solutions.
To get new pairs of values, you have to take an arbitrary value for x, then express y. For example, let's take a value of 7 for the variable x. Then we get an equation with one variable 25 × 7 + 10y = 200 in which we can express y
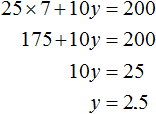
Let x = 15. Then the equation 25x + 10y = 200 will be 25 × 15 + 10y = 200. From this we find that y = -17.5
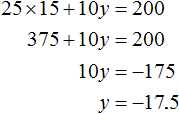
Let x = -3. Then the equation 25x + 10y = 200 will take the form 25 × (-3) + 10y = 200. From this we find that y = -27.5
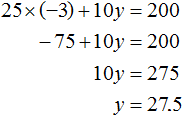
System of two linear equations with two variables
For the equation ax + by = c, you can take an arbitrary value for x and find values for y as many times as you like. An individual equation of this kind will have innumerable solutions.
But it also happens that the variables x and y are connected by not one but two equations. In this case they form what is called a system of linear equations with two variables. Such a system of equations can have one pair of values (or another way: "one solution").
It may also happen that the system has no solutions at all. A system of linear equations can have innumerable solutions in rare and exceptional cases.
Two linear equations form a system when the values of x and y enter into each of these equations.
Let's return to the very first equation 25x + 10y = 200. One of the value pairs for this equation was the pair (6; 5). This is the case where $200 could buy 6 cakes and 5 cups of coffee.
Let's compose the problem so that the pair (6; 5) is the only solution to the equation 25x + 10y = 200. To do this, make another equation that connects the same x cakes and y cups of coffee.
Let's put the text of the problem as follows:
"A student bought several pastries and several cups of coffee for $200. A cake costs $25 and a cup of coffee costs $10. How many cakes and cups of coffee did the student buy if he knows that the number of cakes is one more than the number of cups of coffee?"
We already have the first equation. This equation is 25x + 10y = 200. Now let's make an equation for the condition "the number of cakes is one more than the number of cups of coffee".
The number of cakes is x, and the number of cups of coffee is y. You can write this phrase using the equation x - y = 1. This equation would mean that the difference between the cakes and the coffee is 1.
Or the second equation can be written as x = y + 1. This equation would mean that the number of cakes is one more than the number of cups of coffee. Therefore, one is added to the number of cups of coffee to get equality. This can easily be understood by using the model of scales that we looked at in our study of the simplest problems:

We obtain two equations: 25x + 10y = 200 and x = y + 1. Since the values of x and y, namely 6 and 5, are included in each of these equations, together they form a system. Let us write down this system. If the equations form a system, they are surrounded by a system sign. The system sign is a curly bracket:
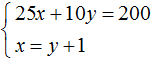
Let's solve this system. This will allow us to see how we arrive at the values of 6 and 5. There are many methods for solving such systems. Let's look at the most popular ones.
Substitution method
The name of this method speaks for itself. Its essence is to substitute one equation into another by first expressing one of the variables.
There is no need to express anything in our system. In the second equation, x = y + 1, the variable x is already expressed. This variable is equal to y + 1. Then substitute this expression into the first equation instead of x
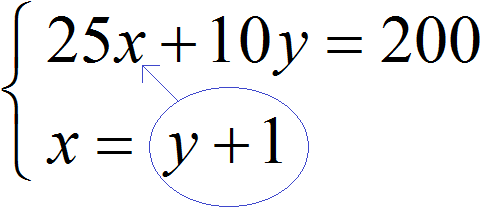
After substituting the expression y + 1 into the first equation instead of x, we get the equation 25(y + 1) + 10y = 200. This is a linear equation with one variable. It is fairly easy to solve such an equation:
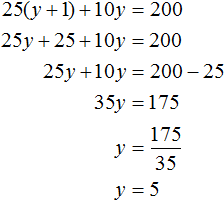
We found the value of the variable y. Now let's substitute this value into one of the equations and find the value of x. To do this, it is convenient to use the second equation x = y + 1. Here we substitute the value of y
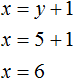
So the pair (6; 5) is a solution to the system of equations, as we intended. We check and make sure that the pair (6; 5) satisfies the system:
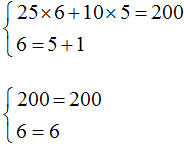
Example 2. Solve the following system of equations by the substitution method:
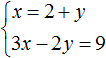
Substitute the first equation x = 2 + y into the second equation 3x - 2y = 9. In the first equation, the variable x equals 2 + y. Substitute this expression into the second equation instead of x
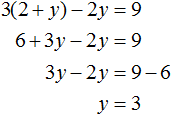
Now let's find the value of x. To do this, substitute the value of y into the first equation x = 2 + y
![]()
So the solution to the system 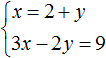 is a pair value (5; 3)
is a pair value (5; 3)
Example 3. Solve the following system of equations by the substitution method:
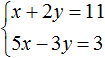
Here, unlike the previous examples, one of the variables is not explicitly expressed.
To substitute one equation for another, you must first express one of the variables.
It is desirable to express a variable that has a coefficient of one. The variable x in the first equation x + 2y = 11 has a coefficient of one.
After expressing the variable x, our system will take the following form:
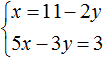
Now substitute the first equation into the second equation and find the value of y
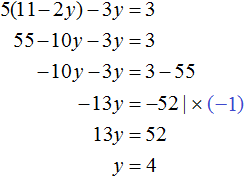
Substitute y into the first equation and find x
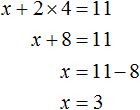
So the solution of the system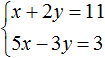 is a pair of values (3; 4)
is a pair of values (3; 4)
Of course, you can also express the variable y. The roots will not change. But if you express y, you get a not-so-simple equation that will take longer to solve. It will look like this:
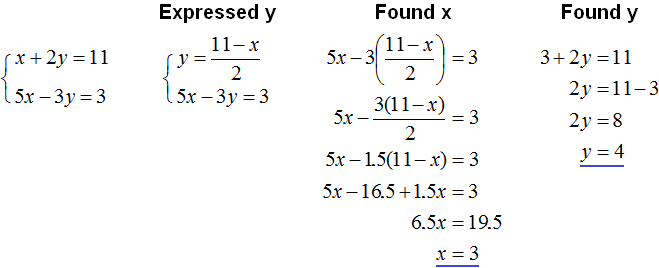
We see that in this example, expressing x is much more convenient than expressing y.
Example 4. Solve the following system of equations by the substitution method:
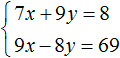
Express x in the first equation. Then the system will take the form:
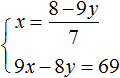
Substitute the first equation into the second equation and find y

Substitute y into the first equation and find x. You can use the original equation 7x + 9y = 8, or you can use the equation X, which expresses the variable ![]() . We will use this equation because it is convenient:
. We will use this equation because it is convenient:
![]()
So the solution of the system 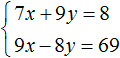 is a pair of values (5; -3)
is a pair of values (5; -3)
Addition method
The addition method consists of adding all the terms of the equation that make up the system. This addition results in a new equation with one variable. And solving such an equation is quite easy.
Let's solve the following system of equations:
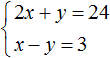
Add the left side of the first equation to the left side of the second equation. And the right part of the first equation with the right part of the second equation. We obtain the following equality:
![]()
Let us give like terms:
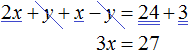
The result is the simplest equation 3x = 27, whose root is 9. Knowing the value of x, you can find the value of y. Substitute the value of x into the second equation x - y = 3. Thus we obtain 9 - y = 3. Hence y = 6.
So the solution of the system 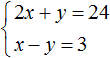 is a pair of values (9; 6)
is a pair of values (9; 6)
Example 2. Solve the following system of equations using the addition method:
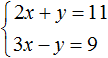
Add the left side of the first equation to the left side of the second equation. And the right part of the first equation with the right part of the second equation. In the resulting equality, add like terms:
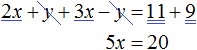
The result is the simplest equation 5x = 20, the root of which is 4. Knowing the value of x, you can find the value of y. Substitute the value of x into the first equation 2x + y = 11. We obtain 8 + y = 11. Hence y = 3.
So the solution of the system 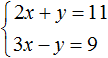 is a pair of values (4;3)
is a pair of values (4;3)
The process of addition is not described in detail. It must be done in the mind. When adding, both equations must be reduced to the canonical form. That is, to the form ax + by = c.
From the examples we looked at, you can see that the main purpose of adding equations is to get rid of one of the variables. But it is not always possible to solve a system of equations by addition right away. Most often the system is first reduced to a form in which the equations that make up the system can be added together.
For example, the system 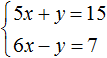 can be solved immediately by addition. By adding both equations, the summands y and -y will disappear, since their sum is zero. This will result in the simplest equation 11x = 22, the root of which is 2. It will then be possible to determine y equal to 5.
can be solved immediately by addition. By adding both equations, the summands y and -y will disappear, since their sum is zero. This will result in the simplest equation 11x = 22, the root of which is 2. It will then be possible to determine y equal to 5.
And the system of equations 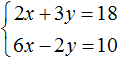 cannot be solved immediately by addition because it will not cause one of the variables to disappear. Addition will result in the equation 8x + y = 28, which has infinitely many solutions.
cannot be solved immediately by addition because it will not cause one of the variables to disappear. Addition will result in the equation 8x + y = 28, which has infinitely many solutions.
If both parts of an equation are multiplied or divided by the same number that is not equal to zero, you will get an equation that is equal to this one. This rule is also true for a system of linear equations with two variables. One of the equations (or both equations) can be multiplied by some number. The result will be an equipotent system whose roots will be the same as the previous one.
Let's go back to the first system (which is given at the beginning of the lesson) 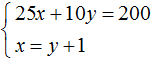 (6; 5).
(6; 5).
Multiply both equations in this system by some numbers. Let's say we multiply the first equation by 2 and the second equation by 3.
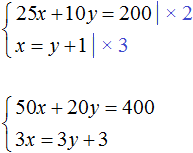
The result is a system of 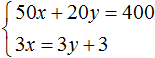
The solution to this system is still a pair of values (6; 5)
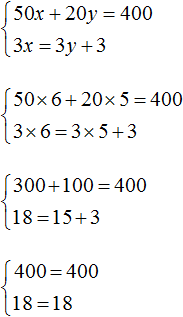
This means that the equations that make up the system can be reduced to a form suitable for the addition method.
Back to the system 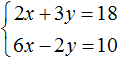 , which we could not solve by addition.
, which we could not solve by addition.
Multiply the first equation by 6 and the second equation by -2
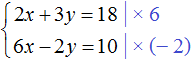
Then we obtain the following system:
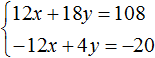
Add the equations that make up this system. Adding the components 12x and -12x will result in 0, adding 18y and 4y will result in 22y, and adding 108 and -20 will result in 88. Then you get the equation 22y = 88, hence y = 4.
If at first it is hard to add equations in your mind, you can write down how the left side of the first equation adds up to the left side of the second equation, and the right side of the first equation adds up to the right side of the second equation:
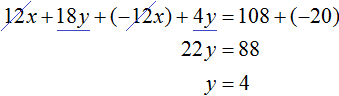
Knowing that the value of the variable y is 4, we can find the value of x. Substitute y in one of the equations, for example in the first equation 2x + 3y = 18. Then we obtain an equation with one variable 2x + 12 = 18. Move 12 to the right side, changing the sign, we get 2x = 6, hence x = 3.
Example 4. Solve the following system of equations using the addition method:
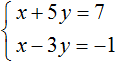
Multiply the second equation by -1. Then the system will take the following form:

Let's add both equations. Adding the components x and -x will result in 0, adding 5y and 3y will result in 8y, and adding 7 and 1 will result in 8. The result is the equation 8y = 8, the root of which is 1. Knowing that the value of y is 1, we can find the value of x.
Substituting y into the first equation, we get x + 5 = 7, hence x = 2
Example 5. Solve the following system of equations using the addition method:
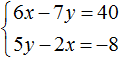
It is desirable that the summands containing the same variables are located under each other. Therefore in the second equation we swap the terms 5y and -2x. As a result, the system will look like this:
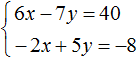
Multiply the second equation by 3. Then the system will look like this:
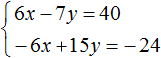
Now add the two equations. As a result of addition we obtain the equation 8y = 16, the root of which is 2.
Substitute y in the first equation to get 6x - 14 = 40. Move the summand -14 to the right side, changing the sign, we obtain 6x = 54. Hence x = 9.
Example 6. Solve the following system of equations using the addition method:
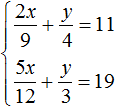
Let's get rid of fractions. Multiply the first equation by 36 and the second equation by 12.
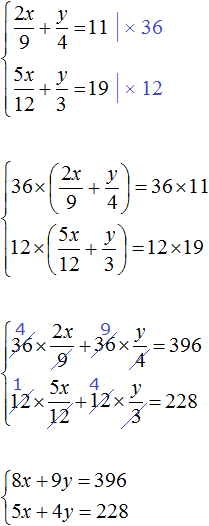
In the resulting system 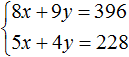 the first equation can be multiplied by -5 and the second equation by 8
the first equation can be multiplied by -5 and the second equation by 8
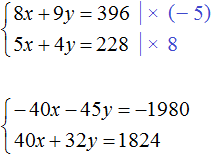
Add the equations in the resulting system. Then we obtain the simplest equation -13y = -156. Hence y = 12. Substitute y into the first equation and find x
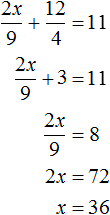
Example 7. Solve the following system of equations using the addition method:
Let us reduce both equations to the normal form. Here it is convenient to apply the rule of proportion in both equations. If the right side of the first equation is represented as ![]() , and the right side of the second equation as
, and the right side of the second equation as ![]() , then the system will take the form:
, then the system will take the form:
We have a proportion. Multiply its extreme and middle terms. Then the system will look like this:
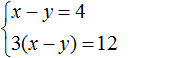
Let us multiply the first equation by -3, and open the brackets in the second equation:
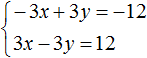
Now let us add the two equations. As a result of adding these equations, we will get an equality in both parts of which is zero:
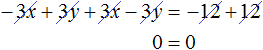
It turns out that the system 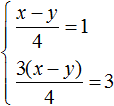 has infinitely many solutions.
has infinitely many solutions.
But we can't just take arbitrary values for x and y. We can specify one of the values, and the other will be determined depending on the value we specify. For example, let x = 2. Let's substitute this value into the system:
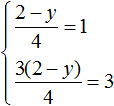
As a result of solving one of the equations, a value for y will be determined that satisfies both equations:
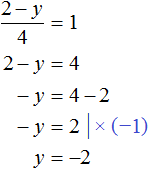
The resulting pair of values (2; -2) will satisfy the system:
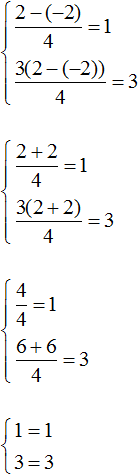
Let us find another pair of values. Let x = 4. Substitute this value into the system:
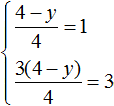
We can quickly determine that the value of y is zero. Then we obtain a pair of values (4; 0) that satisfies our system:
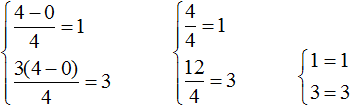
Example 8. Solve the following system of equations using the addition method:
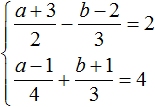
Multiply the first equation by 6 and the second equation by 12
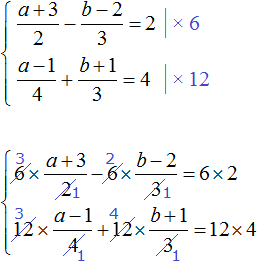
Let's rewrite what we got:
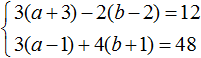
Open the brackets in both equations and give similar summands:
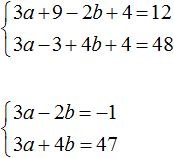
Let us multiply the first equation by -1. Then the system will look like this:
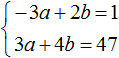
Now add the two equations. The addition results in the equation 6b = 48, the root of which is 8. Substitute b into the first equation and find a
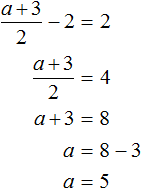
System of linear equations with three variables
A linear equation with three variables includes three variables with coefficients and a free term. In canonical form it can be written as follows:
ax + by + cz = d
This equation has innumerable solutions. By giving two variables different values, a third value can be found. The solution in this case is a triplet of values (x; y; z) that turns the equation into an identity.
If the variables x, y, z are related by three equations, then a system of three linear equations with three variables is formed. To solve such a system, we can apply the same methods that are applied to linear equations with two variables: the substitution method and the addition method.
Example 1. Solve the following system of equations by the substitution method:
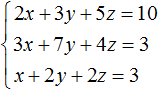
Express x in the third equation. Then the system will look like this:
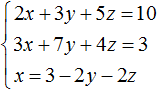
Now let's perform a substitution. The variable x is equal to the expression 3 - 2y - 2z. Substitute this expression into the first and second equations:

Open the brackets in both equations and give similar summands:
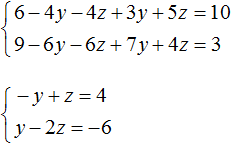
We come to a system of linear equations with two variables. In this case it is convenient to apply the addition method. As a result, the variable y will disappear, and we can find the value of the variable z
![]()
Now let's find the value of y. It is convenient to use the equation -y + z = 4. Substitute in it the value of z
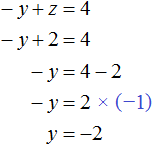
Now let's find the value of x. It is convenient to use the equation x = 3 - 2y - 2z. Substitute in it the values of y and z
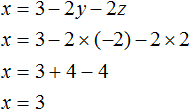
Thus, the triplet of values (3; -2; 2) is a solution to our system. By checking we make sure that these values satisfy the system:
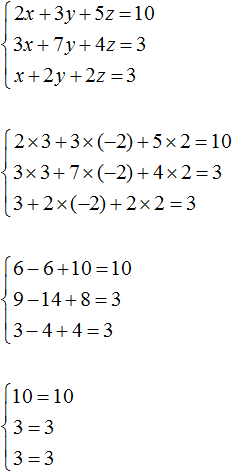
Example 2. Solve the system using the addition method
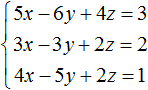
Add the first equation to the second equation multiplied by -2.
If we multiply the second equation by -2, it will be -6x + 6y - 4z = -4. Now add it to the first equation:
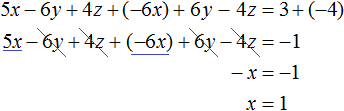
We see that as a result of elementary transformations, the value of the variable x is determined. It is equal to one.
Let us return to the main system. Add the second equation to the third equation multiplied by -1. If we multiply the third equation by -1, it will take the form -4x + 5y - 2z = -1. Now add it to the second equation:
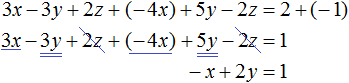
We obtain the equation x - 2y = -1. Let's substitute into it the value of x that we found earlier. Then we can determine the value of y
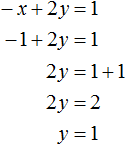
Now we know the values of x and y. This allows us to determine the value of z. Let us use one of the equations included in the system:
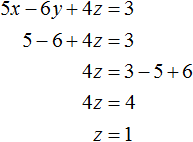
Thus, the triplet of values (1; 1; 1) is a solution to our system. By checking we make sure that these values satisfy the system:
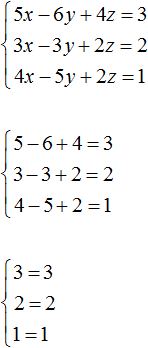
Tasks on composing systems of linear equations
The system of equations task is solved by entering several variables. Then equations are made up based on the conditions of the task. From the equations composed form a system and solve it. After solving the system, you need to check whether its solution satisfies the conditions of the task.
Task 1. A car drove from the city to a farm. On the way back it returned by another road, which was 5 km shorter than the first one. In total the car traveled 35 km in both directions. How many kilometers is the length of each road?
Solution
Let x be the length of the first road, y be the length of the second road. If the car traveled 35 km in both directions, then the first equation can be written as x + y = 35. This equation describes the sum of the lengths of both roads.
We say that the car returned using the road that was shorter than the first road by 5 km. Then the second equation can be written as x - y = 5. This equation shows that the difference between the lengths of roads is 5 km.
Or the second equation can be written as x = y + 5. This is the equation we will use.
Since the variables x and y in both equations stand for the same number, we can form a system of them:
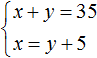
Let us solve this system by any of the methods we studied earlier. In this case it is convenient to use the substitution method, since in the second equation the variable x is already expressed.
Substitute the second equation into the first equation and find y
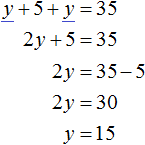
Substitute the found value of y into the second equation x = y + 5 and find x
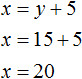
The length of the first road was denoted by the variable x. Now we have found its value. The variable x is 20. So the length of the first road is 20 km.
And the length of the second road was specified by y. The value of this variable is 15. So the length of the second road is 15 km.
Let's check it. First make sure that the system is solved correctly:
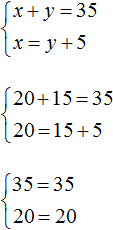
Now check whether the solution (20; 15) satisfies the conditions of the problem.
It was said that the car drove a total of 35 km in both directions. Add the lengths of both roads and make sure that the solution (20; 15) satisfies this condition: 20 km + 15 km = 35 km
The next condition: the car returned by another road, which was 5 km shorter than the first one. We see that the solution (20; 15) satisfies this condition because 15 km is 5 km shorter than 20 km: 20 km - 15 km = 5 km
When compiling the system, it is important that the variables denote the same numbers in all equations that make up the system.
So our system 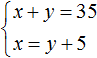 contains two equations. These equations in turn contain the variables x and y, which denote the same numbers in both equations, namely road lengths equal to 20 km and 15 km.
contains two equations. These equations in turn contain the variables x and y, which denote the same numbers in both equations, namely road lengths equal to 20 km and 15 km.
Task 2. The platform was loaded with oak and pine sleepers, a total of 300 sleepers. It is known that all the oak sleepers weighed 1 ton less than all the pine sleepers. Determine how many oak and pine sleepers there were separately, if each oak sleeper weighed 46 kg and each pine sleeper 28 kg.
Solution
Let x oak sleepers and y pine sleepers be loaded on the platform. If the total number of sleepers was 300, then the first equation can be written as x + y = 300.
The oak sleepers all weighed 46x kg, and the pine sleepers weighed 28y kg. Since the oak sleepers weighed 1 ton less than the pine sleepers, the second equation can be written as 28y - 46x = 1000. This equation shows that the difference in mass between the oak and pine sleepers, is 1000 kg.
Tons have been converted to kilograms because the weight of oak and pine sleepers is measured in kilograms.
As a result, we obtain two equations that form a system
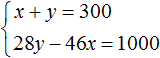
Let us solve this system. Express x in the first equation. Then the system will look like this:
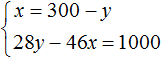
Substitute the first equation into the second equation and find y
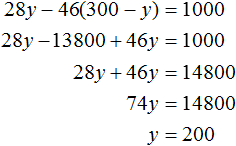
Substitute y into the equation x = 300 - y and find out what x equals
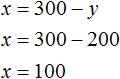
So the platform was loaded with 100 oak and 200 pine sleepers.
Let us check whether the solution (100; 200) satisfies the conditions of the problem. First, let's make sure that the system is solved correctly:

It was said that there were 300 sleepers in total. Add the number of oak and pine sleepers and make sure that the solution (100; 200) satisfies this condition: 100 + 200 = 300.
The following condition: all oak sleepers weigh 1 ton less than all pine sleepers. We see that the solution (100; 200) satisfies this condition as well, since 46 × 100 kg of oak sleepers are lighter than 28 × 200 kg of pine sleepers: 5600 kg - 4600 kg = 1000 kg.
Task 3. We took three pieces of copper-nickel alloy in ratios of 2 : 1, 3 : 1 and 5 : 1 by mass. A 12 kg piece with a copper to nickel ratio of 4 : 1 is alloyed from them. Find the mass of each initial piece if the mass of the first piece is twice the mass of the second one.
Solution
Let x be the mass of the first piece, y be the mass of the second piece, and z be the mass of the third piece. If these pieces are fused into a piece with a mass of 12 kg, then the first equation can be written as x + y + z = 12.
The mass of the first piece is twice the mass of the second piece. Then the second equation can be written as x = 2y.
These two equations are not enough to solve the problem. If we substitute the second equation into the first equation, we get the equation 2y + y + z = 12, whence 3y + z = 12. This equation has innumerable solutions.
Let's make another equation. Let this equation describe the amount of copper taken from each alloy and how much copper was in the resulting alloy.
If the first alloy has mass x, and copper and nickel are in it in the ratio 2 : 1, then we can write that the new alloy contains ![]() copper from the first piece.
copper from the first piece.
If the second alloy has a mass y, and the copper and nickel are in it in the ratio 3 : 1, then we can write that the new alloy contains ![]() copper from the second piece
copper from the second piece
If the third alloy has mass z and the copper and nickel are in the ratio 5 : 1, then we can write that the new alloy contains ![]() copper from the third piece.
copper from the third piece.
The resulting alloy has a mass of 12 kg, and copper and nickel are in it in the ratio 4 : 1. Then we can write that the obtained alloy contains ![]() copper.
copper.
Add ![]() ,
, ![]() ,
, ![]() and equate this sum to 9.6. This will be our third equation:
and equate this sum to 9.6. This will be our third equation:
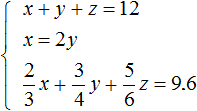
Let's try to solve this system.
First, simplify the third equation. Substitute the second equation into it and see what happens:
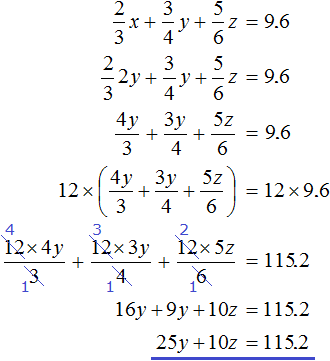
Now in the main system, instead of the equation ![]() , let's write the equation we now have, namely equation 25y + 10z = 115.2
, let's write the equation we now have, namely equation 25y + 10z = 115.2
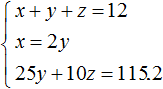
Let's substitute the second equation into the first one:
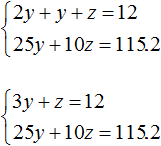
Multiply the first equation by -10. Then the system will look like this:
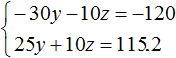
Let us add both equations. Then we obtain the simplest equation -5y = -4.8 from where we find y equal to 0.96. So the mass of the second alloy is 0.96 kg.
Now let's find x. To do this it is convenient to use the equation x = 2y. The value of y is already known. It only remains to substitute it:
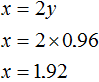
So the mass of the first alloy is 1.92 kg.
Now let's find z. It is convenient to use the equation x + y + z = 12. The values of x and y are already known. Let's substitute them where needed:
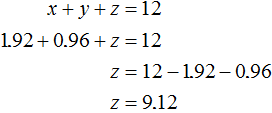
So the mass of the third alloy is 9.12 kg.
Tasks for independent decision
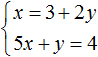
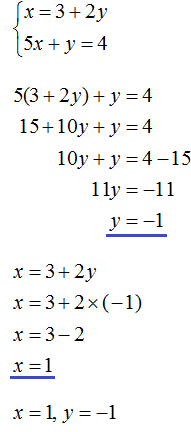
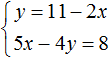
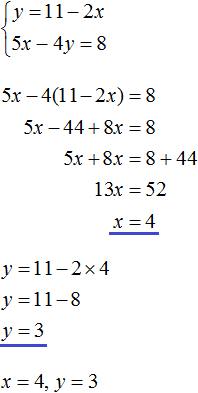
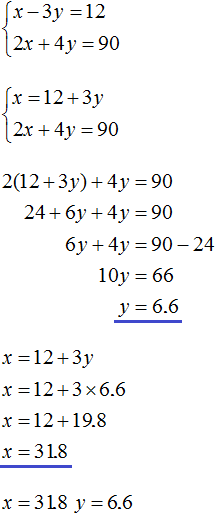
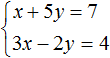
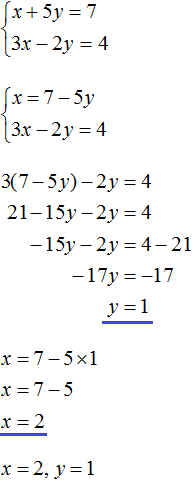
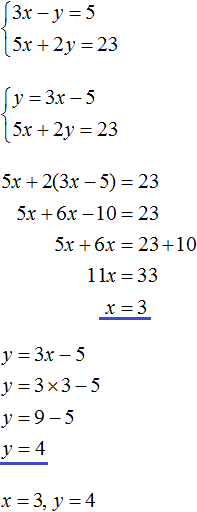
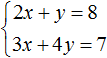
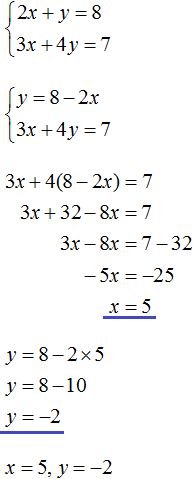
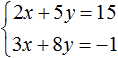
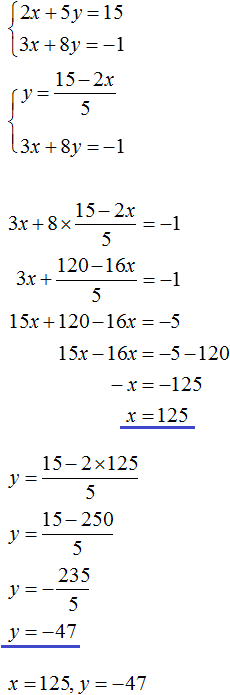
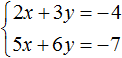
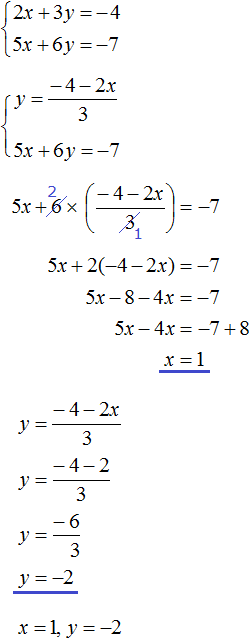
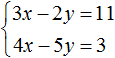
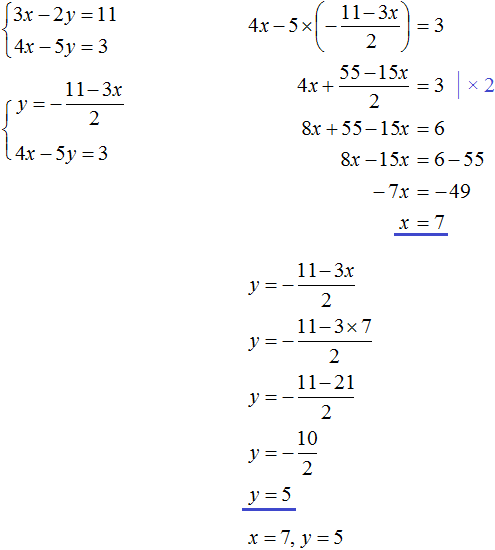
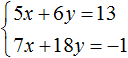
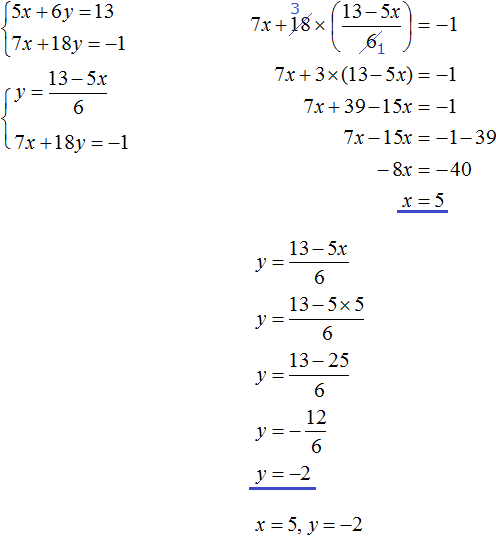
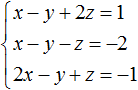
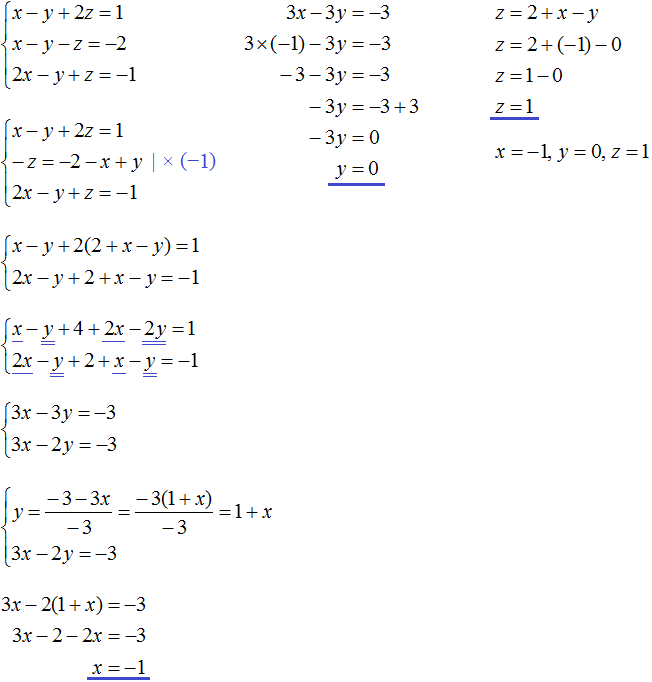
Solution
Let x kg of hay be given to each horse and y kg to each cow. There were 8 horses and 15 cows, which means that all horses were given 8x kg of hay and all cows 15y kg. Together the horses and cows were given 162 kg of hay. Then the first equation can be written as 8x + 15y = 162
It is known that 5 horses received 5x kg of hay, and 7 cows received 7y kg. If 5 horses received 3 kg more hay than 7 cows, then the second equation can be written as 5x - 7y = 3.
Since the variables x and y in both equations represent the same number, we can form a system from them and solve it
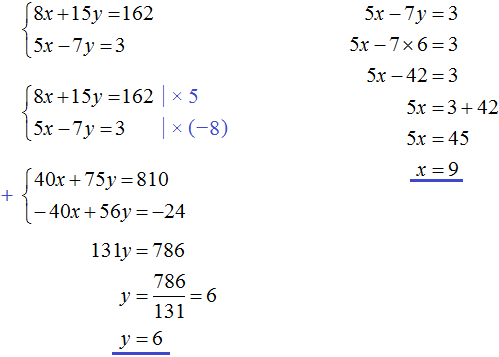
Answer: Every day each horse was given 9 kilograms of hay and each cow 6 kilograms.
Solution
Let x wagons have been loaded to send y tons of cargo. The loading of cargo into the wagons can be described with the help of the ratio ![]() . This ratio shows how many tons of cargo are loaded per wagon.
. This ratio shows how many tons of cargo are loaded per wagon.
In the first case, each car is loaded with 15.5 tons. Then the first equation can be written as ![]() . But the condition says that if we load 15.5 tons per wagon, then 4 tons of cargo will remain unloaded. It means not all cargo will be loaded but only y - 4 tons of cargo. So let us rewrite the first equation as
. But the condition says that if we load 15.5 tons per wagon, then 4 tons of cargo will remain unloaded. It means not all cargo will be loaded but only y - 4 tons of cargo. So let us rewrite the first equation as ![]()
In the second case, 16.5 tons are loaded in each car. Then the second equation can be written as ![]() . But the problem says that if we load 16.5 tons per wagon, then 8 tons of cargo will not be enough to fully load the wagons. This means all cargo will be loaded plus there will be room to load another eight tons of cargo. In other words, in this case we can load y + 8 tons of cargo in the cars. So let's rewrite the second equation as
. But the problem says that if we load 16.5 tons per wagon, then 8 tons of cargo will not be enough to fully load the wagons. This means all cargo will be loaded plus there will be room to load another eight tons of cargo. In other words, in this case we can load y + 8 tons of cargo in the cars. So let's rewrite the second equation as ![]()
Since the variables x and y in both equations denote the same number, you can form a system from them and solve it:
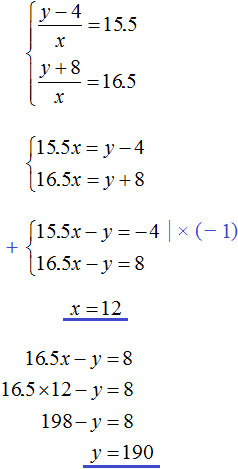
Answer: There were 12 wagons and 190 tons of cargo.
Solution
Let x benches be placed in the hall and y students.
In the first case there are 5 students on each bench. Divide y students by 5 and put them on x benches:
![]()
But the condition says that if we put 5 students per bench, we don't have enough benches. We have only x benches. So that all y students can sit on the benches, we add 8 more benches to x benches.
![]()
In the second case, 6 students are seated on each bench. Divide y students by 6 and seat them on x benches:
![]()
But the condition says that if we put 6 students per bench, then 2 benches will remain free. In this case the students will not sit on x, but on x - 2 benches. Rewrite the second equation as follows:
![]()
Since the variables x and y in both equations denote the same number, you can form a system from them and solve it:
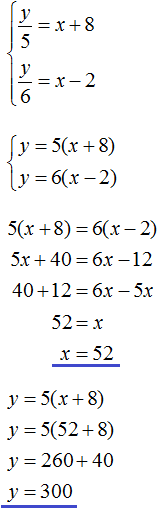
Answer: There were 52 benches and 300 students.
Solution
Let x people participate in the excursion, and the cost of this excursion is y dollars.
If each tour participant contributes $12. 50 cents, the cost would be $12.50x. It is said that in this case $100 is not enough to cover the expenses. To cover the cost, add another $100 to the $12.50x cost
12,50x + 100
The expression 12.50x + 100, like the variable y, describes the same quantity - the cost of the excursion. Therefore, we can connect these two expressions with an equal sign, thus forming the first equation for the system:
12,50x + 100 = y
The task goes on to say that if each participant contributes $16, then there will be a surplus of $12. Since the number of participants is x, the expenses will be 16x. The expense of $16x is $12 more than the planned y dollars. To get the second equation, subtract the $12 surplus from the $16x.
16x − 12
Like the previous expression 12.50x + 100, the expression 16x - 12 describes the cost of the excursion and can be equated with the variable y. This will be the second equation for the system:
16x − 12 = y
We obtained two equations: 12.50x + 100 = y and 16x - 12 = y. The variables x and y denote the same number, so you can form a system from them and solve it:
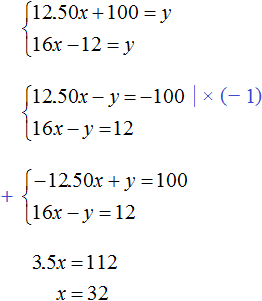
So there are 32 people on the tour.
This task did not ask what the cost of the excursion would be. But for the sake of interest you can calculate them as well:
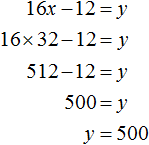
Answer: 32 people participate in the tour.
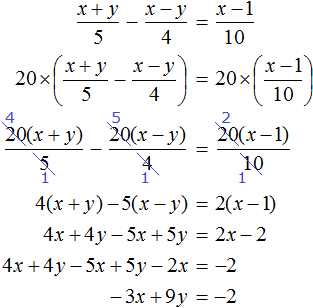
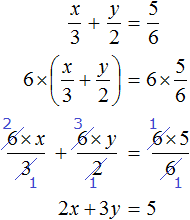
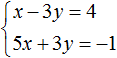
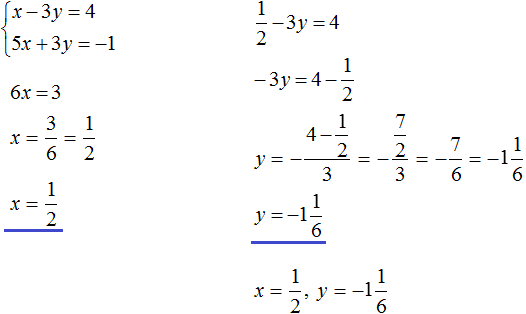
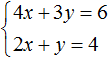
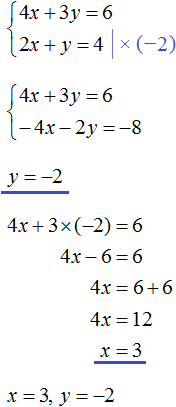
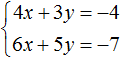
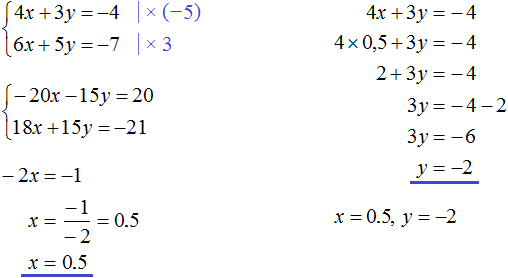
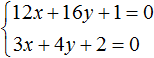
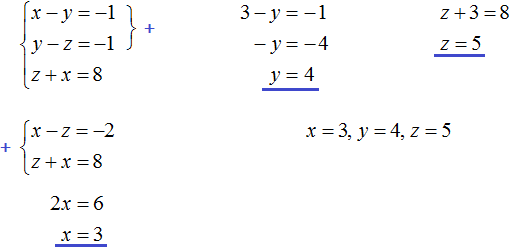
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.