A Ratio is some relationship between entities in our world. It can be numbers, physical quantities, objects, products, or even people.
In mathematics, a ratio is more commonly used as "how many times one number contains another".
For example, if there are four apples and two pears, then the ratio is "four to two " (that is, 4∶2, which is equivalent to the ratio 2∶1), or if we swap apples and pears, "two to four".
The ratio is expressed as a to b (where instead of a and b are any numbers), but more often you can see it like that a : b. There are various ways to read this notation:
- a to b
- ratio of a to b
Let's write down the ratio of four apples and two pears using the ratio symbol (Colon):
4 : 2
This ratio can be read as "four to two" or "the ratio of four apples to two pears" or "four apples to two pears".
If we swap apples and pears, we have a ratio of 2 : 4. This ratio can be read as "two to four" or "two pears to four apples"".
What is a Ratio?
The ratio, as mentioned earlier, is written in the form a:b. It can also be written as a fraction 
. And we know that such a notation in mathematics means division. Then the result of the relation is the quotient of number a and b. Quotient means "how many times" and comes from Latin.
A ratio in mathematics is the quotient of two numbers. Equal quotients correspond to equal ratios.
The ratio lets you know how many times one number contains another
Let's go back to the ratio of four apples to two pears (4 : 2). This ratio lets us know how many apples there are per unit of a pear. By one we mean one pear. First, let's write down the ratio 4 : 2 as a fraction:
This ratio is a division of number 4 by number 2. If we do this division, we get the answer to the question "What is the ratio of apples to pears?"
We got 2. So four apples to two pears (4 : 2)
The diagram shows how four apples and two pears relate to each other. You can see that there are two apples for each pear.
The ratio of can be reversed by writing it as 
. Then we have the ratio of two pears to four apples, or "the ratio of two pears to four apples". This ratio will show how many pears there are per unit of apple. By unit of apple we mean one apple.
To find the value of the fraction you need to remember how to divide a smaller number by a larger one
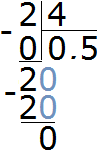
We got 0.5. Let's convert this decimal to an ordinary fraction:
Let's reduce the resulting fraction by 5
The answer is 
(half of a pear). So two pears and four apples (2 : 4) relate to each other in such a way that one apple is half a pear
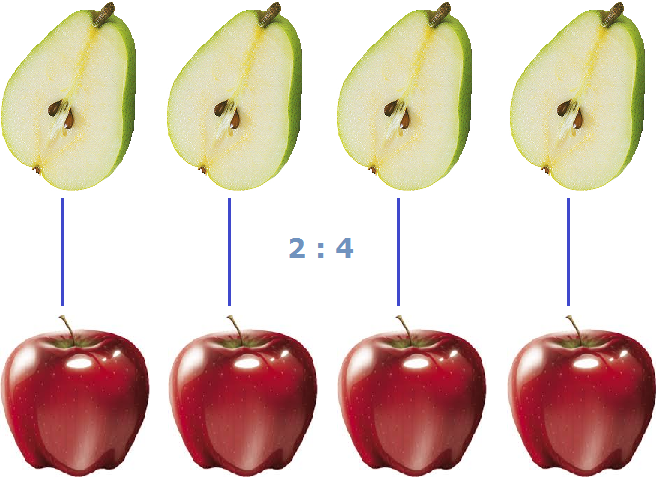
The picture shows whats the retio between two pears and four apples. You can see that for each apple there is a half of a pear.
The numbers that make up the relation are called terms of the ratio.
For example, in the relation 4 : 2, the terms of the ratio are numbers 4 and 2
4 - antecedent and 2 - consequent
Consider other examples of ratios. A recipe is made to cook something. The recipe is based on the ratios between the products. For example, oatmeal usually requires a cup of cereal to two cups of milk or water. The ratio is 1:2 ("one to two" or "one cup of cereal to two cups of milk").
Convert the ratio 1 : 2 into a fraction, we get . Calculating this fraction, we get 0.5. So one glass of cereal and two glasses of milk are related to each other in such a way that one glass of milk is half a glass of cereal.
If we invert the ratio 1 : 2, we get a ratio of 2 : 1 ("two to one" or "two glasses of milk to one glass of cereal"). Convert the ratio 2 : 1 into a fraction, we get 
. Calculating this fraction, we obtain 2. It means that two glasses of milk and one glass of cereal are related to each other in such a way that one glass of cereal has two glasses of milk.
Example 2. There are 15 students in the class. Five of them are boys and 10 are girls. We can write down the ratio of girls to boys 10 : 5 and convert this ratio into a fraction 
. If we calculate this fraction, we get 2. Thats it, girls and boys are related to each other in such a way that there are two girls for every boy
The picture shows how ten girls and five boys are related to each other. You can see that there are two girls for every boy.
It is not always possible to convert the ratio to a fraction and find the quotient. In some cases it will be illogical.
So, if you flip the ratio of you get 
, which is the ratio of boys to girls. If you calculate this fraction you get 0.5. It turns out that five boys relate to ten girls so that each girl is half a boy. Mathematically, of course, this is correct, but in terms of reality it is not quite reasonable, because a boy is a living person and he cannot be just taken and divided like a pear or an apple.
The ability to construct the correct ratio is an important skill when solving problems. So in physics, the ratio of distance traveled to time is the speed of motion.
Distance is denoted by the variable S, time by the variable t, and speed by the symbol v. Then the phrase "the ratio of the distance traveled to time is the speed of motion" will be described by the following expression:
Suppose the car traveled 100 kilometers in two hours. Then the ratio of the hundred kilometers traveled to two hours will be the speed of the car:
Velocity is commonly referred to as the distance traveled by a body in a unit of time. A unit of time is 1 hour, 1 minute, or 1 second. And the ratio, as mentioned earlier, lets you know how much of one entity is per unit of another entity. In our example, the ratio of one hundred kilometers to two hours shows how many kilometers there are for one hour of movement. We see that for every hour of movement there are 50 kilometers
Therefore, speed is measured in km/h, m/min, m/s. The fraction symbol ( / ) indicates the ratio of distance to time: kilometers per hour, meters per minute and meters per second, respectively.
Example 2. The ratio of the cost of goods to their quantity is the price of one unit of goods
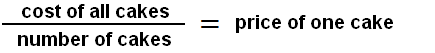
If we took five chocolate cakes from the store and their total cost was $100, we can determine the price of one cake. To do this we need to find the ratio of one hundred dollars to the number of cakes. Then we get that one cake is worth $20.
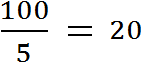
Comparison of values
Earlier we learned that the ratio between quantities of different nature forms is a new quantity. For example, the ratio of distance traveled to time is the speed of motion. The ratio of the value of a commodity to its quantity is the price of one unit of a commodity.
But the ratio can also be used to compare values. The result of a ratio is a number that shows how many times the first value is greater than the second value.
To find out how many times the first value is greater than the second, write the larger value into the numerator and the smaller value into the denominator.
To find out which part of the first value is the second, write a smaller value into the numerator and a larger value into the denominator.
Consider the numbers 20 and 2. Let's find out how many times the number 20 is greater than the number 2. To do this, find the ratio of the number 20 to the number 2. Write number 20 in the numerator and number 2 in the denominator
The value of this ratio is ten
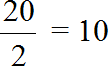
The ratio of number 20 to number 2 is number 10. This number shows how many times the number 20 is greater than the number 2. So the number 20 is ten times the number 2.
Example 2. There are 15 students in the class. 5 of them are boys and 10 are girls. Determine how many times there are more girls than boys.
Write down the ratio of girls to boys. Write the number of girls in the numerator ratio and the number of boys in the denominator:
The value of this ratio is 2. So there are twice as many girls as boys in a class of 15.
It is no longer a question of how many girls there are per boy. In this case the ratio is used to compare the number of girls to the number of boys.
Example 3. What part of the number 20 is equal to the number 2.
Find the ratio of 2 to 20. Write number 2 in the numerator and number 20 in the denominator
To find the value of this ratio, you need to remember how to divide a smaller number by a larger one
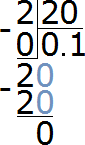
The value of the ratio of the number 2 to the number 20 is the number 0.1
In this case, the decimal 0.1 can be converted to a regular fraction. This answer will be easier to understand:
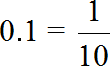
So the number 2 of 20 is one tenth.
You can do a test. To do this, find 
of the number 20. If we have done everything correctly, we should get the number 2
20 : 10 = 2
2 × 1 = 2
We got the number 2. So one tenth of 20 is the number 2. From this we conclude that the problem is solved correctly.
Example 4. There are 15 people in the class. 5 of them are boys and 10 are girls. Determine what part of the total number of students are boys.
Write down the ratio of boys to the total number of students. Write five boys in the numerator and the total number of students in the denominator. The total number of students is 5 boys plus 10 girls, so we write 15 in the denominator of the ratio
To find the value of this ratio, you need to remember how to divide a smaller number by a larger number. In this case, number 5 is divided by number 15.
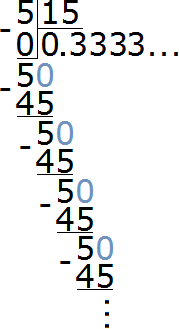
Dividing 5 by 15 results in a periodic fraction. Let's convert this fraction to an ordinary fraction
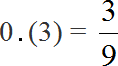
Let's reduce the resulting fraction by 3
The final answer is 
. So the boys make up one-third of the class.
The figure shows that in a class of 15 students, one-third of the class is made up of 5 boys.
If we find of the 15 students to check, we get 5 boys
15 : 3 = 5
5 × 1 = 5
Example 5. How many times 35 is bigger than the number 5 ?
Write the ratio of number 35 to number 5. Write number 35 in the numerator and number 5 in the denominator, but not vice versa.
The value of this ratio is 7. So the number 35 is seven times larger than number 5.
Example 6. There are 15 people in the class. 5 of them are boys and 10 are girls. Determine what part of the total number are girls.
Write down the ratio of girls to the total number of students. Write ten girls in the numerator of the ratio and the total number of students in the denominator. The total number of students is 5 boys plus 10 girls, so we write 15 in the denominator of the ratio
To find the value of this ratio, you need to remember how to divide a smaller number by a larger number. In this case, the number 10 must be divided by the number 15
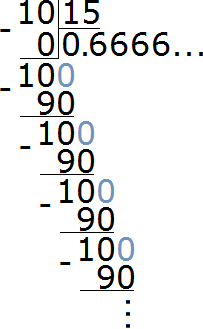
Dividing 10 by 15 results in a periodic fraction. Let's convert this fraction to an ordinary fraction
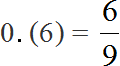
Let's reduce the resulting fraction by 3
The final answer is 
. So girls make up two-thirds of the class.
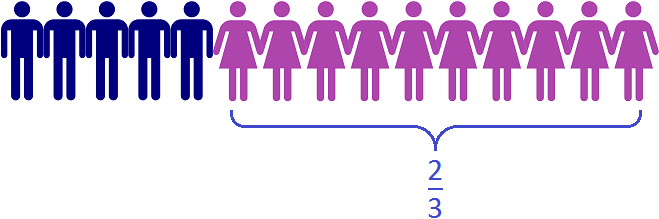
The figure shows that in a class of 15 students, two-thirds of the class consists of 10 girls.
If we find of 15 schoolchildren to check, we get 10 girls
15 : 3 = 5
5 × 2 = 10
Example 7. What part of 25 centimeters is equal to 10 centimeters?
Write the ratio of ten centimeters to twenty-five centimeters. Write 10 cm in the numerator and 25 cm in the denominator
To find the value of this ratio, you need to remember how to divide a smaller number by a larger number. In this case, we need to divide the number 10 by the number 25
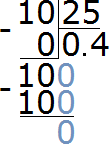
Convert the resulting decimal fraction into an ordinary fraction
Let's reduce the resulting fraction by 2
Got the final answer 
. So 10 cm is of 25 cm.
Example 8. How many times 25 cm is greater than 10 cm
Write down the ratio of twenty-five centimeters to ten centimeters. Write 25 cm in the numerator and 10 cm in the denominator
Let's find the value of this ratio
The answer is 2.5. So 25 cm is 2.5 times larger than 10 cm (two and a half times).
Important note. When finding the ratio of physical quantities of the same name, these quantities must be expressed in the same unit of measurement, otherwise the answer will be incorrect.
For example, if we are dealing with two lengths and want to know how many times the first length is bigger than the second, then both lengths must first be expressed in one unit (km, m, miles).
Example 9. How many times is 150 cm greater than 1 meter?
First, let's make both lengths be expressed in one unit. To do this, let's convert 1 meter to centimeters. One meter is one hundred centimeters.
1 m = 100 cm
Now find the ratio of one hundred and fifty centimeters to one hundred centimeters. Write 150 centimeters in the numerator and 100 centimeters in the denominator
Let's find the value of this ratio
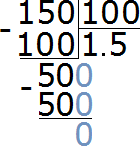
The answer is 1.5. So 150 cm is 1.5 times more than 100 cm (one and a half times).
And if we didn't translate meters into centimeters and immediately tried to find the ratio of 150 cm to one meter, we would have the following:
It would turn out that 150 cm is one hundred and fifty times more than one meter, and this is incorrect. Therefore, it is necessary to pay attention to the units of physical quantities that are involved in the ratio. If these quantities are expressed in different units, then in order to find the ratio of these quantities, you must switch to one unit of measurement.
Example 10. Last month the bank director's salary was $25,000, and this month the salary increased to $27,000. Determine how many times new salary is larger than the old one.
Write down the ratio of twenty-seven thousand to twenty-five thousand. We write 27000 in the numerator and 25000 in the denominator
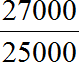
Let's find the value of this ratio
The answer was 1.08. That means that the wage increased by 1.08. In the future, when we become familiar with percentages, we will express indicators such as wages in percentages.
Example 11. An apartment building is 80 meters wide and 16 meters high. Whats the ratio between the width of the house and its height?
Write down the ratio of the width of the house to its height:
The value of this ratio is 5. So the width of the house is five times its height.
Properties of Ratio
-
- A ratio remains the same if its terms of the ratio are multiplied or divided by the same non-zero number,
- a/b = pa/pb = qa/qb , p, q ≠0
- a/b = (a/p) / (b/p) = (a/q) / (b/q) , p, q ≠0
- Two ratios in their fraction notation can be compared just as we compare real numbers.
- a/b = p/q ⟺ aq = bp
- a/b > p/q ⟺ aq > bp
- a/b < p/q ⟺ aq < bp
- If two ratios a/b and c/d are equal
- a/b = c/d ⟹ b/a = d/c (Invertendo)
- a/b = c/d ⟹ a/c = b/d (Alternendo)
- a/b = c/d ⟹ (a+b)/b = (c+d)/d (Componendo)
- a/b = c/d ⟹ (a-b)/b = (c-d)/d (Dividendo)
- A ratio remains the same if its terms of the ratio are multiplied or divided by the same non-zero number,
The ratio will not change if its terms of the ratio are multiplied or divided by the same number.
This is one of the most important properties of the ratiios follows. We know that if the quotient and the divisor are multiplied or divided by the same number, the quotient will not change. And since a relation is nothing more than a division, the property of the quotient works for it as well.
Let's return to the ratio of girls to boys (10 : 5). This ratio shows that there are two girls for every boy. Let's check how the property of the ratio works, namely let's try to multiply or divide its members by the same number.
In our example, it is more convenient to divide the terms of the ratio by their greatest common divisor (GCD).
The GCD of the terms 10 and 5 is the number 5. Therefore, it is possible to divide the terms of the ratio by the number 5
We have a new ratio of . This is the ratio of two to one (2:1). This ratio, like the previous 10:5 ratio, shows that there are two girls for every one boy.
The figure shows a ratio of 2 : 1 (two to one). As in the past ratio of 10 : 5, there are two girls for one boy. In other words, the ratio has not changed.
Example 2. One class has 10 girls and 5 boys. The other class has 20 girls and 10 boys. How many times there are more girls than boys in the first grade? How many times there are more girls than boys in the second grade?
There are twice as many girls as boys in both classes because the ratios of 
and 
are the same number.
The ratio property allows you to create different models that have similar parameters to the real object. Suppose that an apartment building is 30 meters wide and 10 meters high.
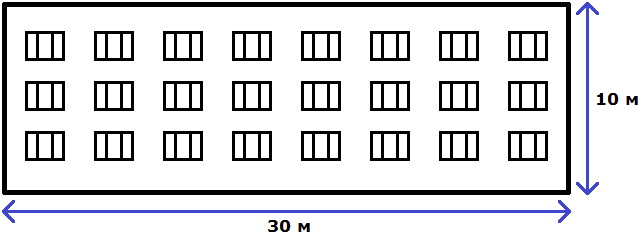
To draw a similar house on paper, you need to draw it in the same ratio of 30 : 10.
Let's divide both terms of this ratio by the number 10. Then we get a ratio of 3 : 1. This ratio equals 3, just as the previous ratio equals 3
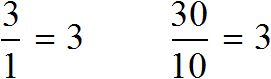
Let's convert meters to centimeters. 3 meters is 300 centimeters, and 1 meter is 100 centimeters.
3 m = 300 cm
1 m = 100 cm
We have a ratio of 300 cm : 100 cm. Divide the terms of this ratio by 100. We have a ratio of 3 cm : 1 cm. Now we can draw a house with a width of 3 cm and a height of 1 cm
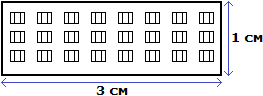
Of course the drawn house is much smaller than the real house, but the ratio of width to height remains the same. This allowed us to draw a house as similar to the real house as possible
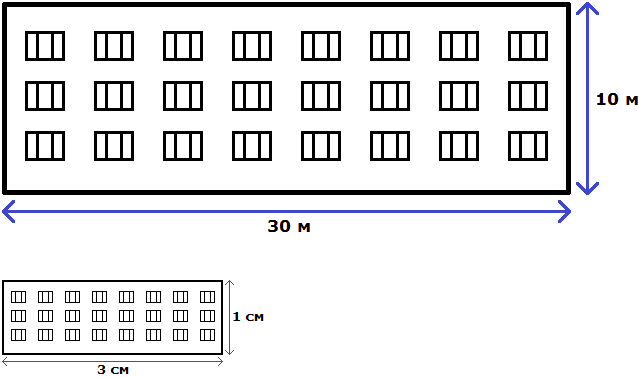
The relation can also be understood in another way. Initially it was said that the real house has a width of 30 meters and a height of 10 meters. The total is 30+10, that is 40 meters.
This 40 meters can be understood as 40 parts. The ratio of 30 : 10 indicates that 30 parts are for the width and 10 parts are for the height.
Then the terms of the 30 : 10 ratio were divided by 10. The result is a ratio of 3 : 1. This ratio can be understood as 4 parts, three of which are width and one of which is height. In this case, you usually want to know how many specific meters are accounted for the width and height.
In other words, you need to find out how many meters are in 3 parts and how many meters are in 1 part. First you need to find out how many meters there are for one part. To do this, divide the total of 40 meters by 4, because in the ratio 3 : 1 there are only four parts
40 m : 4 = 10 m
Then use multiplication to determine how many meters come to the width and height. The terms that are given in the ratio are used as a factor.
Determine how many meters account for the width:
10 m × 3 = 30 m
Let's determine how many meters account for the height:
10 m × 1 = 10 m
Several terms in the ratio
If more than one member is given in a ratio, they can be understood as parts of something.
Example 1. Eighteen apples were bought. The apples were given to mom, dad, and daughter in the ratio 2 : 1 : 3. How many apples did each person get?
The ratio 2 : 1 : 3 indicates that Mom got 2 parts, Dad got 1 part, and Daughter got 3 parts. In other words, each member of the 2 : 1 : 3 ratio is a certain fraction of 18 apples:
If you add up the terms of the ratio 2 : 1 : 3, you can find out how many parts there are in total:
2 + 1 + 3 = 6 (parts)
Let's find out how many apples per one part. To do this, divide 18 apples by 6
18 : 6 = 3 (apples for one part)
Now let's determine how many apples each person got. Multiplying three apples by each member of the ratio 2 : 1 : 3, you can determine how many apples did Mom get, how many apples did Dad get, and how many apples did Daughter get.
Let's find out how many apples did Mom get:
3 × 2 = 6 (apples)
Let's see how many apples did Dad get:
3 × 1 = 3 (apples)
Let's see how many apples did Daughter get:
3 × 3 = 9 (apples)
Example 2. New silver (alpaca) is an alloy of nickel, zinc, and copper in the ratio 3 : 4 : 13. How many kilograms of each metal must be taken to make 4 kg of new silver?
4 kilograms of new silver will contain 3 parts nickel, 4 parts zinc, and 13 parts copper. First, find out the total number of parts in four kilograms of silver:
3 + 4 + 13 = 20 (parts)
Let's determine how many kilograms will be in one part:
4 kg : 20 = 0.2 kg
Determine how many kilograms of nickel will be contained in 4 kg of new silver. The ratio 3 : 4 : 13 indicates that three parts of the alloy contain nickel. Therefore we multiply 0.2 by 3:
0.2 kg × 3 = 0.6 kg nickel
Now let's determine how many kilograms of zinc will be contained in 4 kg of new silver. The ratio 3 : 4 : 13 indicates that four parts of the alloy contain zinc. Therefore we multiply 0.2 by 4:
0.2 kg × 4 = 0.8 kg of zinc
Now let's determine how many kilograms of copper will be contained in 4 kilograms of new silver. The ratio 3 : 4 : 13 states that thirteen parts of the alloy contain copper. Therefore we multiply 0.2 by 13:
0.2 kg × 13 = 2.6 kg of copper
So to get 4 kg of new silver, you have to take 0.6 kg of nickel, 0.8 kg of zinc, and 2.6 kg of copper.
Example 3. Brass is an alloy of copper and zinc whose masses are 3 : 2. It takes 120 g of copper to make a piece of brass. How much zinc is required to make this piece of brass?
Determine how many grams of alloy are in a piece. The condition says that it takes 120 grams of copper to make a piece of brass. It also says that three parts of the alloy contain copper. If we divide 120 by 3, we find out how many grams of the alloy are in one piece:
120 : 3 = 40 grams per part
Now let's determine how much zinc is needed to make a piece of brass. To do this, multiply 40 grams by 2, because the ratio of 3 : 2 indicates that two parts contain zinc:
40 g × 2 = 80 grams of zinc
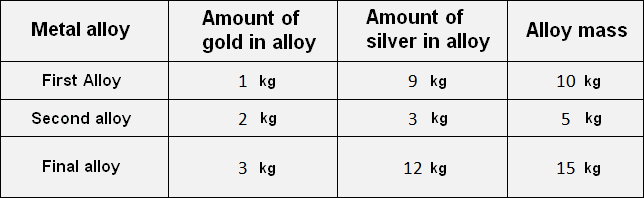
Example 4. Two alloys of gold and silver are taken. One has a 1 : 9 ratio of these metals and the other has a 2 : 3 ratio. How much of each alloy do you need to take to get 15 kg of a new alloy that has gold and silver in a 1 : 4 ratio?
Solution
15 kg of the new alloy must consist of a ratio of 1 : 4. This ratio indicates that one part of the alloy will be gold, and four parts will be silver. There are five parts in all. This can be schematically represented as follows
Let's determine the mass of one part. To do this, first add up all the parts (1 and 4), then divide the mass of the alloy by the number of these parts
1 + 4 = 5
15 kg : 5 = 3 kg
One part of the alloy will have a mass of 3 kg. Then 15 kg of the new alloy will contain 3 × 1 = 3 kg of gold and silver 3 × 4 = 12 kg of silver.
Therefore, we need 3 kg of gold and 12 kg of silver to obtain an alloy with a mass of 15 kg.
Now let's answer the question of the problem - "How much of each alloy should be taken?"
We will take 10 kg of the first alloy, because gold and silver in it are in the ratio of 1 : 9. That is, this first alloy will give us 1 kg of gold and 9 kg of silver.
For the second alloy, we will take 5 kilograms, because gold and silver are in the ratio of 2 : 3. So this second alloy will give us 2 kg of gold and 3 kg of silver.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.