In this lesson we will learn how to divide numbers. Division of numbers is not an easy operation to learn and use. We recommend that you be patient enough to finish this lesson.
What is division?
Definition. Division is the process of dividing something. Division involves three components: the dividend, the divisor, and the quotient. The dividend is the number or quantity that is being divided. The divisor is the number that indicates how many parts the dividend is divided into. The quotient is the resulting value or answer.
For example, suppose we have four apples:

Divide them equally among the two friends. Then the division will show how many apples each will get. It is easy to see that everyone will get two apples:
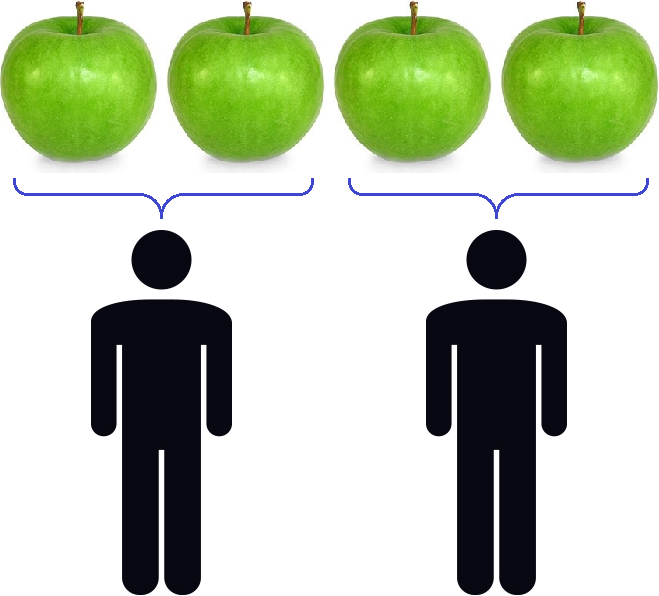
The process of dividing four apples by two friends can be described by the following expression:
![]()
In this example, the dividend is apples. The divisor is two friends, showing how many parts to divide the 4 apples into. The quotient is two apples, showing how many each got..
There are other ways to talk about division. Let us return to the previous expression 4 : 2 = 2. We can look at the divisor 2 and ask the question "how many twos are in a four?" and the answer is "two twos". Indeed, if we add two twos, we get the number 4
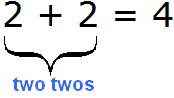
In the four-apple situation, you could ask the question "how many times two apples are contained in four apples" and answer, "two times".

To learn how to divide, you need to know the multiplication table well. Why multiplication? Because we are talking about division. The fact is that division is the inverse of multiplication. This phrase can be understood in the literal sense. For example, if 2 x 5 = 10, then 10 : 5 = 2.
![]()
You can see that the second expression is written in reverse order. If we have two apples and we want to increase them by a factor of five, we write 2 x 5 = 10. That would make ten apples. Then, if we want to put the ten apples back down to two apples, we write 10 : 5 = 2.
The division sign looks like a colon : but you can also find colons and dashes ?
In writing, it makes more sense to use a colon because it looks neater.
Division with a remainder
Definition. The remainder is what is left of the action of division undivided.
For example, five divided by two would be two and one in the remainder:
5 : 2 = 2 (1 in the remainder)
You can check it by multiplication:
(2 x 2) + 1 = 5
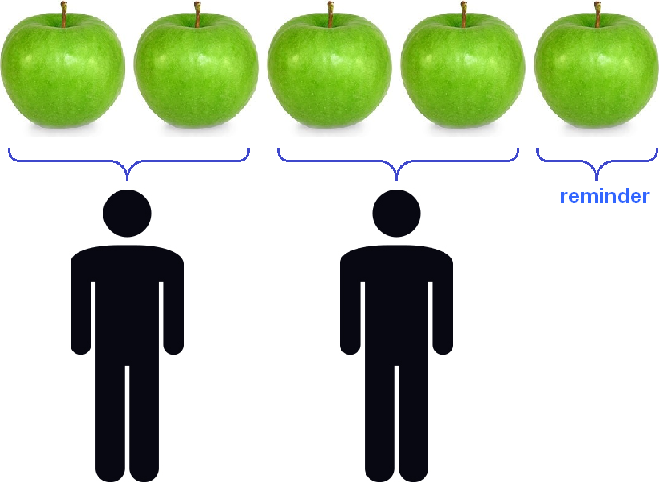
Suppose we have five apples

Divide them equally among the two friends. But you can't divide equally five whole apples. Then this division will show that everyone will get two apples, and one apple will be in the remainder:
Long division (Column division)
When you need to divide a large number, it is a must to use this method.
Before long division, you must know:
- normal division of small numbers;
- division with a remainder;
- long multiplication;
- long subtraction.
Let's look at the long division with a simple example. Let us find the value of the expression 9 : 3. The long division is written as follows:
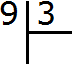
Example 1. Everyone knows that nine divided by three is three. The answer (quotient) is written like this:
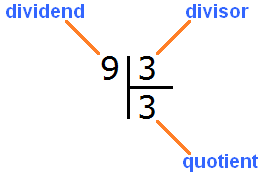
To check if there is a remainder of division, you need to multiply the quotient by the divisor and write the answer under the quotient. The quotient in this case is 3, and the divisor is also 3. Multiply these two numbers: 3 x 3 = 9. This gives us 9. Write this nine under the dividend:
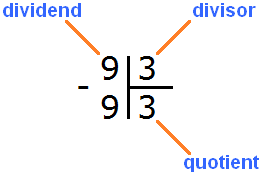
Now from the divisor we subtract the nine we wrote under it: 9 - 9 = 0. The remainder is zero. Simply put, there is no remainder. This completes the division successfully:
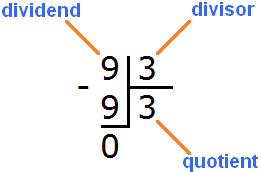
Example 2. Find the value of the expression 8 : 3
Eight times three is not a simple division. The multiplication table won't help either. In this case the remainder of division will be present.
Let's first write this expression with long divison:
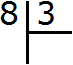
Now we have to ask the question, "How many threes are in an eight?" An eight contains two threes. This can even be seen firsthand if we think of an eight as eight sticks:
At school, the quotient is picked up by the matching method. We've all heard phrases like "take one," "take two," or "take three. We have just such a case. We take two by answering that there are two threes in an eight. We write the two in the right-hand corner:
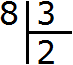
Now take out the remainder. To do this, multiply the quotient by the divisor (2 by 3) and write the resulting number under the divisor:
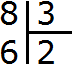
Then we subtract 6 from 8. The resulting number is the remainder:
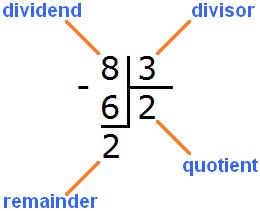
8 : 3 = 2 (2 in the remainder)
Check: (2 x 3) + 2 = 6 + 2 = 8
Dividing a multi-digit number by a single-digit number
This topic may seem confusing the first time. Don't despair and give up on learning. Understanding will come in any case. If not immediately, then a little later. The main thing is not to give up and continue to study hard.
In previous examples, we divided a single-digit number by a single-digit number, and this did not give us too much trouble. Now we are going to divide a multi-digit number by a single-digit number.
If you do not understand what single and multi-digit numbers are, we advise you to study the previous lesson, which is called multiplication.
To divide a multi-digit number by a single-digit number, you must first look at the first digit of that multi-digit number and see if it is greater than the divisor. If it is greater, then divide, and if not, then check if the first two digits of the multi-digit number are greater than the divisor. If the first two digits are greater than the divisor, then divide, and if not, then check if the first three digits of the multi-digit number are greater than the divisor. And so on until the first division is done.
Is it difficult? Not at all, if we look at some examples.
Example 1. Find the value of the expression 25 : 3
25 is a multi-digit number, and 3 is a single-digit number. Apply the rule. Look at the first digit of a multi-digit number. The first digit is 2. Is two more than three? No. So we look at the first two digits of a multi-digit number. The first two digits form the number 25. Is twenty-five more than three? Yes, it is greater. So we divide the number 25 by 3. Write this expression with help of long divison and start dividing:
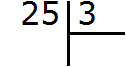
How many threes are in 25? If the answer is difficult at first, you can look at the multiplication table by three. There you need to find a product that is less than 25, but very close to it or equal to it. If you find such a product, you need to take from there the multiplier that gave such a product:
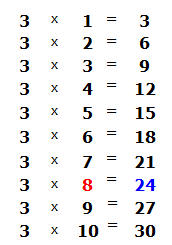
This is a multiplication table by three. In it, you need to find a product that is less than 25, but very close to it or equal to it. Obviously, this is the product of 24, which is highlighted in blue. From this expression, you need to take away the multiplier that gave that product. This is the multiplier 8, which is shaded in red.
This eight answers the question of how many threes are in the number 25. Write it like this:

Now take out the remainder. To do this, multiply the quotient by the divisor (8 by 3) and write the resulting number under the divisor:
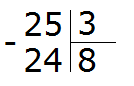
Now subtract the number 24 from the divisor and get 1. This will be the remainder:
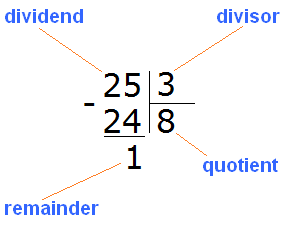
25 : 3 = 8 (1 left over)
(8 x 3) + 1 = 24 + 1 = 25
The last remainder is always less than the divisor. If the last remainder is greater than the divisor it means that division is not complete.
In the example above, the last remainder was 1 and the divisor was 3. One is less than three, so division is complete. The last remainder smaller than the divisor indicates that it does not contain numbers equal to the divisor.
In our example, if you ask the question "how many threes are in a unit?", the answer is "none," because a unit contains no threes because it is less than a three.
Example 2. Divide 326 by 4.
Look at the first digit of 326. The first digit is 3. Is it larger than the divisor of 4? No. Then we check the two digits of the dividend. The two digits of the dividend form number 32. Is it greater than the divisor of 4? Yes, it is. That's why we divide it. Write this expression:
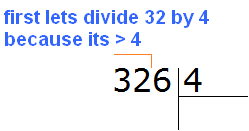
Now we ask the question, "How many fours are in the number 32? There are eight fours in the number 32. This can be seen in the multiplication table by four:
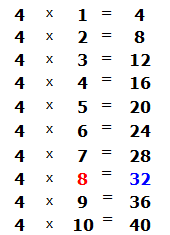
This eight, which is highlighted in red, answers the question how many fours are in 32. Write it:
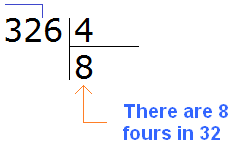
Now multiply 8 by 4 to get 32 and write that number under the divisor. Then subtract this number from 32. We obtain 0. Since the solution is not yet complete, do not write zero:

The first number 32 is divided. It remains to divide the remaining 6. To do this, tear down that six:
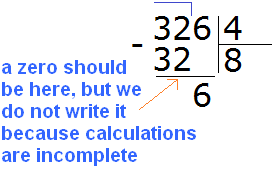
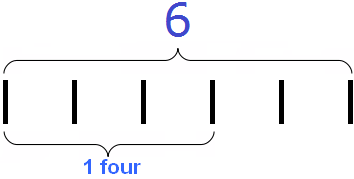
Now divide 6 by 4. To do this, we ask the question, "How many fours are in a six?" There is one four in a six; you can see this by picturing the six as six sticks:
Write one in the right-hand corner of our answer:
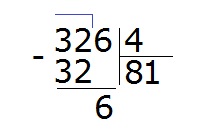
Now multiply our one by the divisor (1 by 4) and write the resulting number under the six:
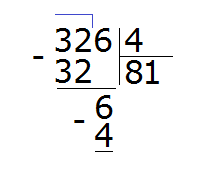
Then we subtract 4 from 6 and get the number 2, which is the remainder:
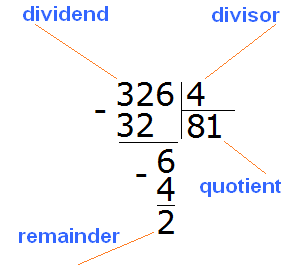
We got 326 : 4 = 81 (2 in the remainder)
Check: (81 x 4) + 2 = 324 + 2 = 326
The procedure in which we look for the first number to divide by comparing whether it is greater than the divisor or less is called finding the first incomplete dividend.
Let's go back to the previous example 326 : 4. The first incomplete dividend in this expression was 32 because we divided it first.
And in the example 25 : 3, the first incomplete dividend was 25.
Example 3. Find the value of the expression 384 : 5
Write this expression:
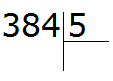
First we find the first incomplete dividend. The first digit is smaller than the divisor, so we check two digits. The two digits together form the number 38, which is greater than the divisor. This number will be the first incomplete dividend. We will divide it by the divisor first:
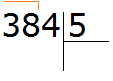
How many fives are in the number 38? If it is difficult to answer right away, you can look at the multiplication table for five and find a product that is less than 38, but very close to it or equal to it. Having found such a product, you need to take from there the multiplier that will answer our question:
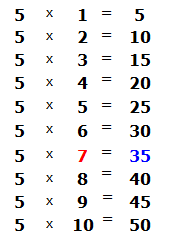
This is the multiplication table by five. Find a product that is less than 38, but very close to it or equal to it. Obviously, it is the product of 35, which is highlighted in blue. From this expression, we take away the multiplier that gave that product. This is the multiplier 7, which is highlighted in red.
This seven answers the question of how many fives are in the number 38. Write this seven in the right corner of our example:
Multiply 7 by 5 to get 35 and write it under 38:
Now subtract 35 from 38 to get 3:
This triplet is the remainder that was left undivided by dividing 38 by 5. But you can see that we still have to divide 4. This 4 we will take down and divide together with the 3:
You can see that after we took down the four, it together with the three formed the number 34. We will divide this number 34 by 5. To do this, we again ask the question, "how many fives are in the number 34?" You can look again at the multiplication table for five and find a product that is less than 34, but very close to it or equal to it:
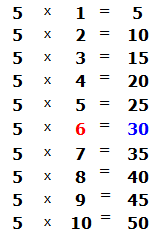
You can see that in the multiplication table by five, the number 30 is less than our 34, but close to it. From this expression we take the multiplier 6, which answers our question. Write this six in the right corner of our example:
Now multiply 6 by 5 to get 30 and write that number under 34:
Now subtract 30 from 34 and you get 4. This four is the remainder of dividing 384 by 5.
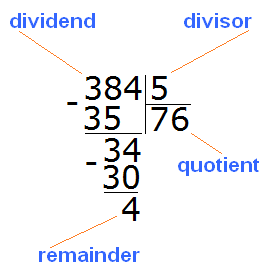
384 : 5 = 76 (and 4 left over)
Check: (76 x 5) + 4 = 380 + 4 = 384
Example 4. Find the value of expression 8642 : 4
This example is a little more complicated. Write this expression in the corner:
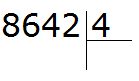
The first digit of 8 is greater than the divisor. This eight will be the first incomplete dividend. Dividing 8 by 4, we get 2
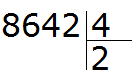
Now multiply 2 by 4 and you get 8. Write this eight under the first incomplete dividend:
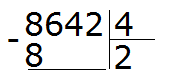
Pull out the remainder: 8 - 8 = 0. The residue from dividing 8 by 4 is zero. We do not write down zero, because the solution of the example is not complete.
Next, we take down the number 6 and divide it by the divisor, and get 1
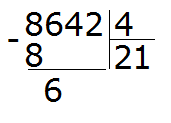
Multiply 1 by 4 to get 4. Write this four under the six that has been taken down. Then take out the remainder by subtracting four from six:
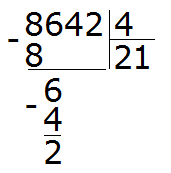
The remainder is 2. This is the remainder left over from dividing 6 by 4.
Now we take the next digit out of the divisor. This is the digit 4. This four, together with the previous residue 2, makes 24. We divide it by the divisor. We get 6
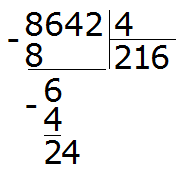
Multiply 6 by 4 to get 24. Write this number under 24
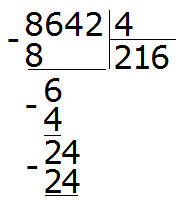
Pull out the remainder: 24 - 24 = 0. Zero is the residue from dividing 24 by 4. Zero, as we have already agreed, is not written down. Then we take down the last digit of 2
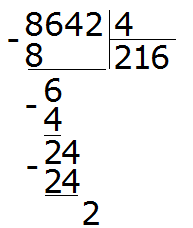
Here begins the most interesting part. The two is the last digit that we took down, and we have to divide it by the divisor 4. But the point is that the two is smaller than the four, and the divisor must be larger than the divisor. If we ask the question "how many fours are in a two?", the answer is zero because a two is less than a four and cannot contain a number greater than itself.
Therefore, two divided by four is zero:
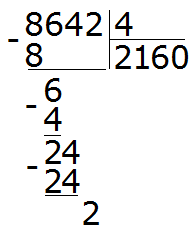
Multiply 0 by 4 to get 0. Write that 0 under the 2:
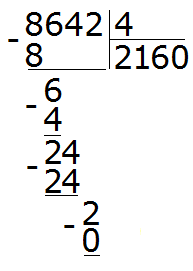
Now find the remainder: 2 - 0 = 2. The two is the remainder of dividing 8642 by 4. This completes the example:
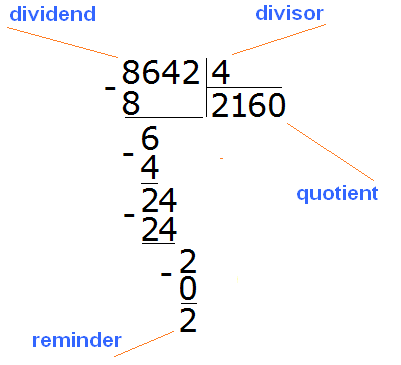
8642 : 4 = 2160 (2 left over)
Check: (2160 x 4) + 2 = 8640 + 2 = 8642
Dividing numbers ending in zeroes
To divide a number that has a zero at the end, you need to temporarily discard that zero, do the usual division, and add that zero to the answer.
For example, divide 120 : 3
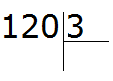
How many threes are there in the number 120? To answer this question, we temporarily discard the zero at the end of 120 and divide 12 by 3 to get 4. Then we add that zero to the quotient. We end up with 40:
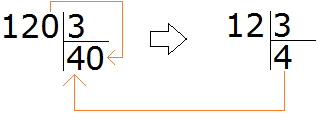
Now multiply the quotient by the divisor (40 by 3) and you get 120. Then we find the remainder: 120 - 120 = 0. The remainder is zero. Example complete.
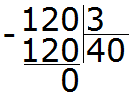
120 : 3 = 40
Check 40 x 3 = 120.
Such simple examples do not need to be solved with a corner. It is enough to know the multiplication table. Next, simply add zeros at the end. For example:
12 : 3 = 4 (the divisor without zeroes at the end)
120 : 3 = 40 (this one has one zero at the end).
1200 : 3 = 400 (here the subject has two zeros)
12000 : 3 = 4000 (this has three zeroes)
There's a bit of a catch to this method. If you have noticed, by dividing these numbers, we are referring to the multiplication table. Imagine dividing 400 by 5.
We can reason the old way - discard all zeros temporarily and divide regular numbers. But what happens if we discard all the zeros in the number 400? We find that we divide 4 by 5, which is unacceptable. In this case, we should discard only one zero and divide 40 by 5 instead of 4 by 5.
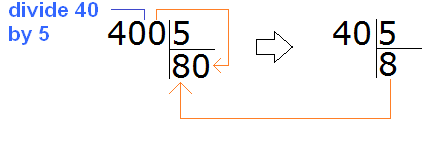
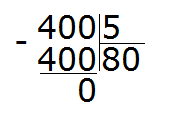
This method works only if you can apply the multiplication table smoothly. In other cases, you have to look for workarounds by calculating the quotient with a column division.
For example, find the value of the expression 1400 : 5. Here, discarding zeros will not give us anything. This example must be solved with a column division, or you can assemble the answer like a construction set. Let's look at the second way.
What is 1400?
Recall the place value. 1400 is one thousand and four hundred:
1000 + 400 = 1400
You can separately divide 1000 by 5 and 400 by 5:
1000 : 5 = 200
400 : 5 = 80
and add up the results:
200 + 80 = 280
Total: 1400 : 5 = 280
Let's solve the same example with a column division:
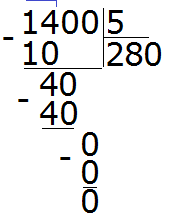
Dividing a multi-digit number by a multi-digit number
Here you will have to strain your brain and squeeze the most out of it, because dividing a multi-digit number by a multi-digit number is not that easy.
The principle of division is the same as before. Here you also need to find the first incomplete dividend. Here you can also find the remainder of the division.
First, we introduce a new concept - a round number. A round number is a number that ends in zero. For example, the following numbers are round:
10, 20, 30, 500, 600, 1000, 13000
Any number can be turned into a round number. To do this, the first digits forming the largest digit are left unchanged, and the remaining digits are replaced by zeros.
For example, let's turn number 19 into a round number. The first digit of the number 1 forms the most significant digit (digit of tens) - the digit is left as is, and the remaining 9 is replaced by zero. The result is 10.
Another example. Let's turn number 125 into a round number. The first digit 1 forms the largest place (place of hundreds) - we leave the digit unchanged, and the remaining 25 digits are replaced with zeros. The result is 100.
Another example. Turn number 2431 into a round number. The first digit 2 is the largest digit (thousand digit), leave it unchanged, and replace the remaining digits 431 with zeros. The final result will be 2000.
Another example. Let's turn number 13735 into a round number. The first two digits of 13 form the large digit (tens of thousands) - leave these two digits unchanged, the remaining digits of 735 are replaced with zeros. The result is 13000.
Warning. In what follows, the concepts of round numbers and the translation of any number into a round number will be generalized.
Let's go back to dividing multi-digit numbers by multi-digit numbers. The difficulty in dividing such numbers is that the result of division must be found by "guessing". To do this, they use various methods, for example, turn the dividend and the divisor into round numbers, so that it would be easier to estimate how many times the divisor is contained in the dividend in your mind (For example, how many times 17 contains in 85 (85 / 17)? We can round and calculate 80 / 20, because its easier to do so. )
Example 1. Find the value of the expression 88 : 12
Write this expression with a corner:
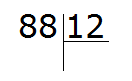
Ask the question how many numbers are 12 in the number 88? It's hard to answer from the first time. You have to reason.
We remember from school that the quotient was guessed by saying "take two" or "take three".
Let's try to guess the quotient. Unfortunately, you can't just take it from the sky. The quotient must be such that when it is multiplied by the divisor, the result is a number that is less than the divisor, but very close to it or equal to it.
Let's assume that the quotient is 2. Multiply this quotient by the divisor 12
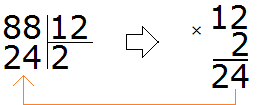
What does this give us? The resulting number is smaller than the divisor, but close to it? No. It is certainly less than the divisor 88, but very far from it. So two as a quotient doesn't fit. Let's guess the next number. Let's say the quotient is 5.
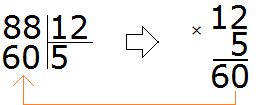
What does this give us? The resulting number is of course smaller, but it is not close to the divisible 88. So five as a quotient doesn't fit either. Let's try to take 8 at once.
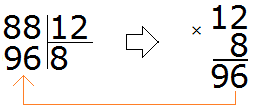
This time the resulting number is greater than the divisible number. And it should be less than the divisible, but very close to it or equal to it. So eight as a quotient doesn't fit either.
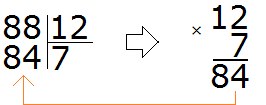
We finally found the right quotient! By multiplying the quotient 7 by the divisor 12, we get 84, which is less than the divisor, but close to it. Now we find the remainder of the division. To do this, we subtract 84 from 88 and get 4.
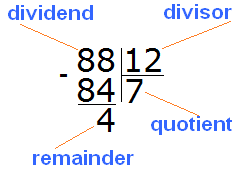
88 : 12 = 7 (4 left over)
Check: (12 x 7) + 4 = 84 + 4 = 88
As you can see from the example, it takes precious time to pick up a private. If we are sitting for a test or an exam, where every minute is important, this method will obviously not help us.
To save time, you can turn the divisor and the divisor into round numbers and then divide those round numbers. Dividing round numbers is much easier and more convenient.
For example, to divide 90 by 10, just take away the zeros from both numbers and divide 9 by 1. The result will be 90 : 10 = 9.
The number of zeroes to be discarded must be strictly the same. For example, if we divide 900 by 90, then we drop a zero from each number, because 900 has two zeros, and 90 has only one. By dropping a zero from each number, we get the expression 90 : 9 = 10. We end up with 900 : 90 = 10.
There is also nothing complicated about dividing round numbers. Try to understand it. If you don't understand it, study it several times. This is very important.
Here are some examples of how to divide round numbers. The zeros to be discarded are shaded in gray:
800 : 10 = 80 (discard each zero and divide 80 by 1, you get 80)
800 : 80 = 10 (truncated by zero and divided 80 by 8, so we have 10)
900 : 10 = 90 (truncated by zero and divided by 90 divided by 1, so you get 90)
400 : 50 = 8 (truncated by zero and divided 40 by 5, yielding 8)
320 : 80 = 4 (zero was truncated and 32 divided by 8, yielding 4)
If you've noticed, it all comes down to the multiplication table in the end. That's why schools require you to know it by heart. We require it too, although we don't force it.
Now let's solve the previous example 88 : 12 where we were struggling to find the quotient by guessing. First, turn the divisor and the divisor into round numbers.
The round number for 88 is 80.
And the round number for 12 is 10.
Now divide the resulting round numbers:
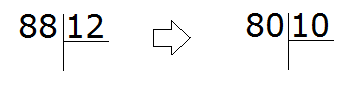
Now we check if the quotient is correct. To do this, we multiply the quotient by the divisor (8 by 12). We already checked the eight as a quotient when we solved this example by guessing. It did not fit, because after multiplying it by the divisor, we got the number 96, which is larger than the divisor. But the quotient 7, which is less than eight by only one, did fit.
From this, we can conclude that in the expression 88 : 12, the quotient obtained by turning the divisor and the divisor into round numbers is greater by only one. Our task is to reduce this quotient by one.
So let's reduce 8 by one: 8 - 1 = 7. Seven is the quotient. Write it in the right corner of our example:

As you can see, we solved this example much faster this way.
Example 2. Find the value of the expression 1296 : 144
Write this expression in the corner. Immediately we find the first incomplete dividend. It is formed by all four digits of the divisor:
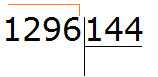
This is dividing a multi-digit number by a multi-digit number. Let's apply the method we just learned. Let's turn the divisor and the divisor into round numbers and then divide them.
For the divisor 1296, the round number is 1000. And for the divisor 144, the round number is 100.
Divide 1000 by 100, and we get 10. Check the resulting 10 by multiplying it by the divisor 144
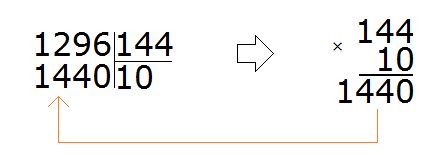
The tens don't fit, because multiplication produces a number that is greater than the divisor.
Let's try to take 9 by decreasing the tens by one.
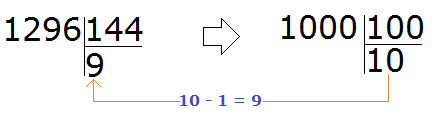
We check the nine. To do this we multiply it by the divisor:
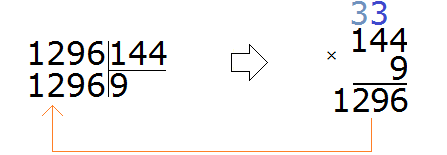
Beautiful! The resulting number was not only closer to the divisible, but also equal to it. This means that the division was done without a remainder. Complete this example by subtracting the resulting number 1296 from 1296
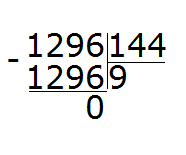
1296 : 144 = 9
Check: 144 x 9 = 1296
Example 3. Let's try to solve a big and complicated example 227,492 : 331
Write this expression in the corner. Immediately determine the first incomplete dividend. It is formed by the first four digits of the divisible 2274. So we first divide 2274 by 331. Let's turn them into round numbers.
For 2274, the round number is 2000. And for 331 the round number is 300.
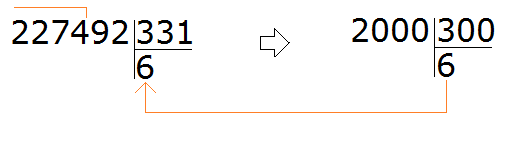
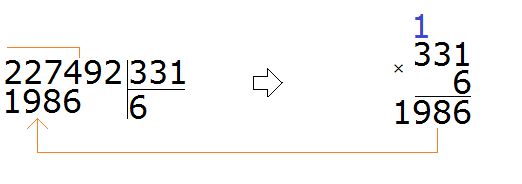
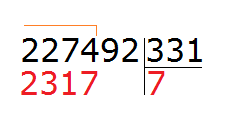
If we were to take a 7 and check that 7, we would get 2317, which is greater than the divisor, and that is not allowed.
We continue to solve our example. Subtract 1986 from 2274, we get 288:
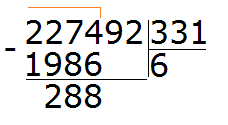
288 is the remainder of dividing 2274 by 331. Next, to continue dividing, you need to take down a nine:
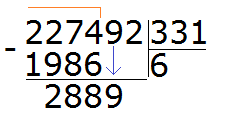
Now we have to divide 2889 by 331. Turn them into round numbers and divide them. Immediately check the quotient obtained in this way:
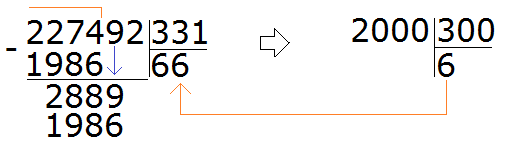
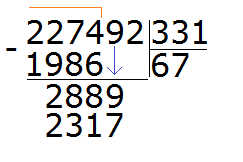
We checked the seven. Again we got a number that is far from the divisor 2889. So the seven does not fit either. Let's check the eight:

The eight fits. It answers the question of how many numbers 331 are in 2889. If we took nine each, then multiplying by the divisor, we would get the number 2979, which is already more than the divisor 2889.
Now we take out the remainder of the division of 2889 by 331. To do this, we subtract 2648 from 2889 and get 241.
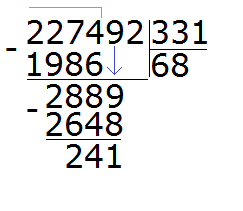
241 is the remainder of dividing 2889 by 331. To continue dividing, remove 2 from the main divisor:
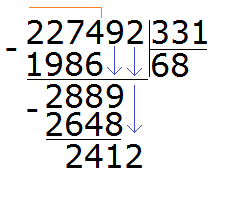
Now divide 2412 by 331. Let's take 7
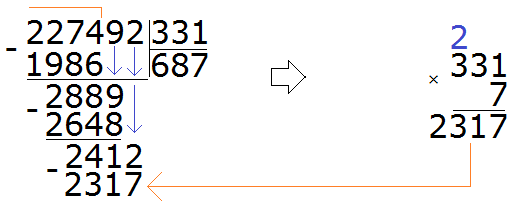
Now we find the last residue. To do this, we subtract 2317 from 2412 and get 95. This completes the example:

227492 : 331 = 687 (95 in balance)
Check: (331 x 687) + 95= 227 397 + 95 = 227 492
This is the end of this lesson. Don't be upset if you don't immediately learn how to divide numbers by a corner. This skill is built up over time, combined with intensive training. Mistakes are not terrible. The most important thing is to understand.
Note that in this lesson we will only look at division with a remainder. We will consider division without the remainder in the next lessons. This is done in order not to make learning difficult. As they say, all in good time.
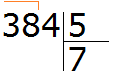
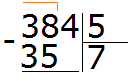
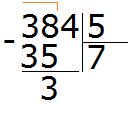
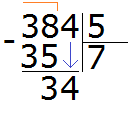
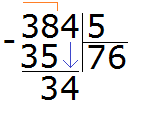
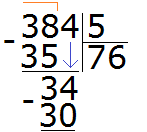
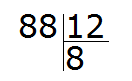
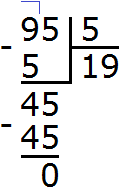
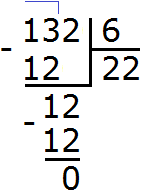
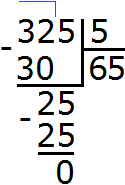
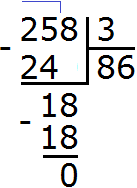
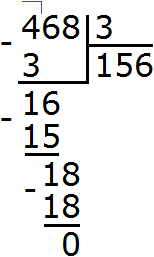
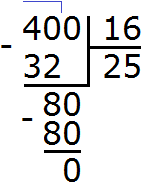
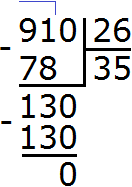
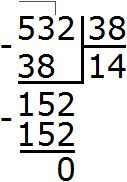

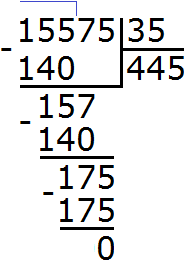
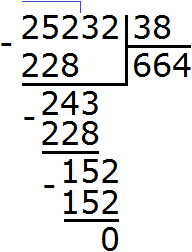
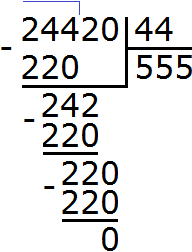
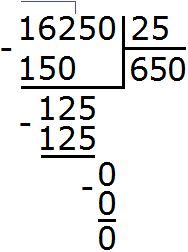
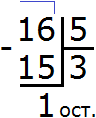
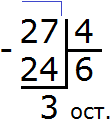
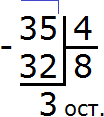
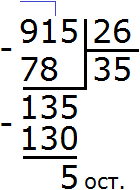
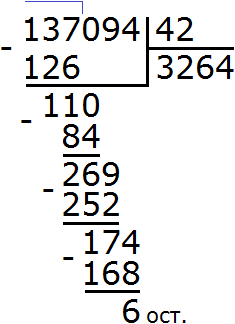
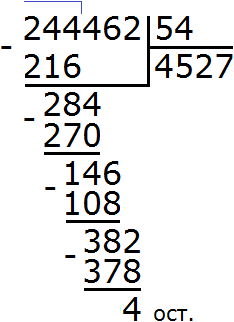
Comments
After many thoughts of quitting, I decided that If I wanted to get anything out of it I should at least try and learn math from the basics since I miss every key concept ever and it shows even when I try to program because I lack every logic possible and don't even know how to write down a basic expression(well now I kinda do, thanks to you!).
I started from chapter one and I want to slowly do them all.
Feels like too much to learn IOT otherwise. I feel like I need to understand math.
This website really come in clutch during a horrible down.
Thanks Paul for giving me the hope that maybe I can really do it if I try hard enough!
You are absolutely right, corrected the mistake, thank you!
I have a question about terminology though:
Shouldn't the first incomplete divisor be called the first incomplete dividend? Since the divisor (the number be divide with) is a fixed number, while it is the dividend (the number that is being divided) that we sort of "section off" while performing the calculation. Or is there another way I ought to understand the "incomplete" part of that term?
30
8/246
6 remaining
is this now wrong do I have to change to this different system used in the lesson.
Your website is much appreciated. It is a request that the above statement be explained.
Gratefully yours,
Alphonso