A quadratic equation with an even second coefficient

If in the quadratic equation ax² + bx + c = 0 the second factor b is even, then the solution of this equation can be simplified a little. The discriminant for such an equation can be calculated by the formula D₁ = k² − ac, and the roots by the formulas 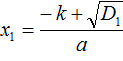 and .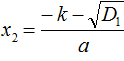

Examples

Solve the quadratic equation x² + 6x − 16 = 0. In this equation, the second coefficient is even. To use the formulas for the even coefficient, we first need to know what the variable k is equal to.

Any even number n can be represented as the product of number 2 and number k, that is, 2k.

n = 2k

For example, the number 10 can be represented as 2 × 5.

10 = 2 × 5

In this product k = 5.

The number 12 can be represented as 2 × 6.

12 = 2 × 6

In this product k = 6.

The number -14 can be represented as 2 × (-7)

In this product k = -7.

As we see, the factor 2 does not change. Only the factor k changes.

In the equation x² + 6x − 16 = 0, the second coefficient is 6. This number can be represented as 2 × 3. In this product k = 3. Now we can use the formulas for the even coefficient.

Find the discriminant by the formula D₁ = k² − ac

D₁ = k² − ac = 3² − 1 × (−16) = 9 + 16 = 25

Now let's calculate the roots using the formulas: 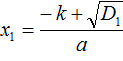 and .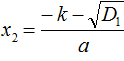

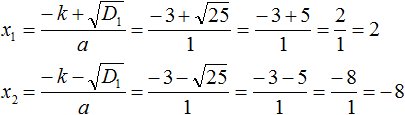
So the roots of the equation x² + 6x - 16 = 0 are the numbers 2 and -8.

Unlike the standard formula for calculating the discriminant (D=b² - 4ac), the formula D1 = k² - ac does not need to multiply the number 4 by ac.

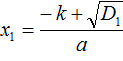And unlike formulas  and , formulas  and 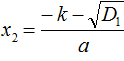 do not contain the factor 2 in the denominator, which again frees us from additional calculations.

Example 2. Solve the quadratic equation 5x² − 6x + 1=0

The second coefficient is an even number. It can be represented as 2 × (-3). That is, k = -3. Find the discriminant by the formula D₁ = k² − ac

D₁ = k² − ac = (−3)² − 5 × 1 = 9 − 5 = 4

The discriminant is greater than zero. So the equation has two roots. To calculate them we use formulas 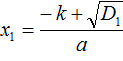 and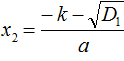 

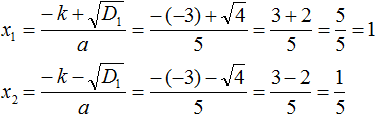
Example 3. Solve the quadratic equation x² − 10x − 24 = 0

The second coefficient is an even number. It can be represented as 2 × (-5). That is, k = -5. Find the discriminant by the formula D₁ = k² − ac

D₁ = k² − ac = (−5)² − 1 × (−24) = 25 + 24 = 49

The discriminant is greater than zero. So the equation has two roots. To calculate them we use formulas 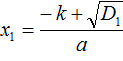 and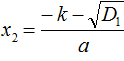 

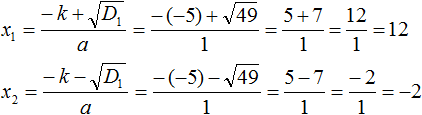
The usual way to determine the number k is to divide the second coefficient by 2.

Indeed, if the second quotient b is an even number, it can be represented as b = 2k. In order to express the factor k from this equality, one must divide the product of b by the factor 2

For example, in the previous example you could simply divide the second factor -10 by 2 to determine the number k

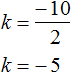
Example 4. Solve a quadratic equation

The coefficient of b is . This expression consists of the multiplier 2 and the expression . That is, it is already represented as 2k. It turns out that 

Find the discriminant by the formula D₁ = k² − ac

The discriminant is greater than zero. So the equation has two roots. To calculate them we use formulas 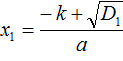 and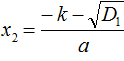 

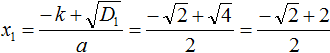
Calculating the root of the equation produces a fraction that contains the square root of 2. The square root of 2 can only be extracted approximately. If you do this approximate extraction and then add the result to 2, and then divide the numerator by the denominator, you get a not very nice answer.

In such cases, the answer is written down without performing approximate calculations. In our case, the first root of the equation is .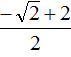

Calculate the second root of the equation:

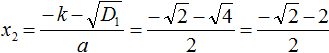
How to derive formulas

Let's visualize how formulas for calculating the roots of a quadratic equation with an even second coefficient appeared.

Consider the quadratic equation ax² + bx + c = 0. Assume that the coefficient of b is an even number. Then it can be denoted as 2k

b = 2k

Replace in the equation ax² + bx + c = 0 the quotient of b by the expression 2k

ax² + 2kx + c = 0

Now let's calculate the discriminant using the previously known formula:

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac

In the resulting expression, take the common factor 4 out of the brackets.

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac = 4(k² − ac)

What can be said about the resulting discriminant? If the second coefficient is even, it consists of factor 4 and the expression k² − ac.

In the expression 4(k² − ac) the factor 4 is constant. So the sign of the discriminant depends on the expression k² − ac. If this expression is less than zero, then D will be less than zero. If the expression is greater than zero, then D is greater than zero. If the expression is equal to zero, then D will be equal to zero.

That is, the expression k² − ac is the discriminant. Such a discriminant is usually denoted by the letter D₁

D₁ = k² − ac

Now let's see how formulas 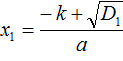 and 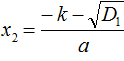 are derived

In our equation ax² + bx + c = 0 the quotient of b is replaced by the expression 2k. Use the standard formulas for calculating the roots. That is, we use formulas  and . Only instead of b we substitute 2k. Also note that D equals the expression 4(k² − ac).

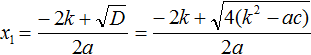
But it was said earlier that the expression k² − ac is denoted by D₁. Then in our transformations we should make this substitution as well:

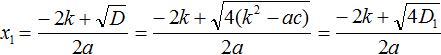
Now let's calculate the square root located in the numerator. This is the square root of the product - it is equal to the product of the roots. Let's rewrite the rest without changing:

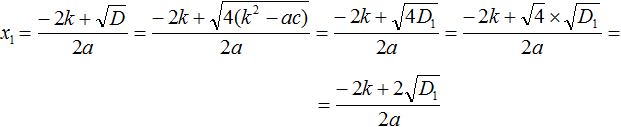
Now, in the resulting expression, take the common factor 2 out of the brackets.

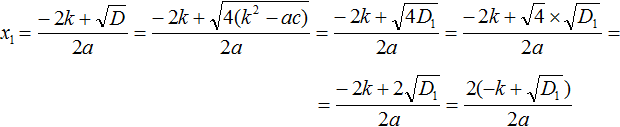
Let's reduce the resulting fraction by 2

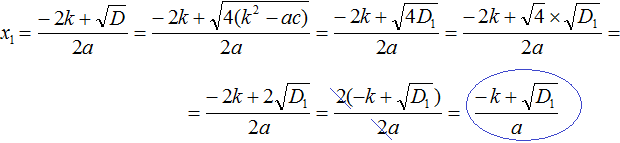
Similarly, the formula for calculating the second root is derived:

Tasks for independent decision

Task 1. Solve the equation:

Solution:

Answer: 1; 0,6

Show Solution

Task 2. Solve the equation:

Solution:

Answer:

Show Solution

Task 3. Solve the equation:

Solution:

Answer: 1; −1.4

Show Solution

Task 4. Solve the equation:

Solution:

Answer:

Show Solution

Task 5. Solve the equation:

Solution:

Answer:

Show Solution

Task 6. Solve the equation:

Solution:

Answer:

Show Solution

Task 7. Solve the equation:

Solution:

Answer:

Show Solution

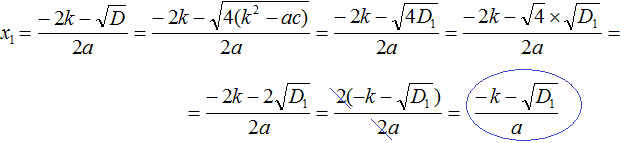
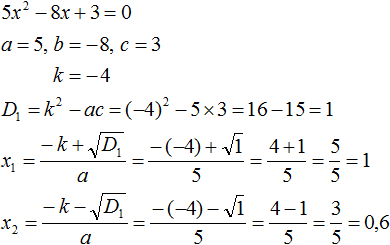
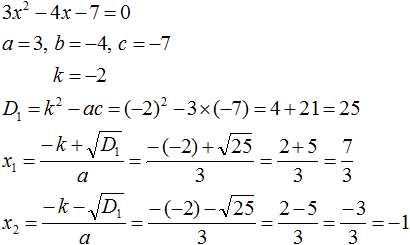
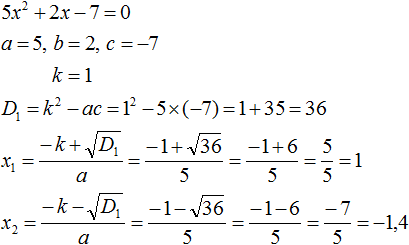
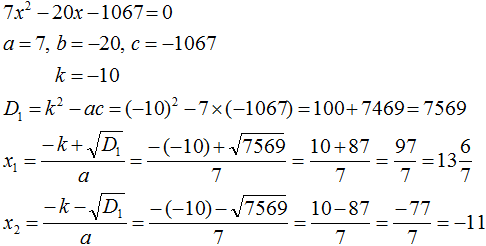
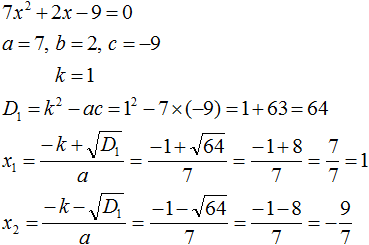
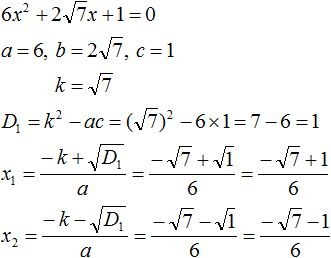
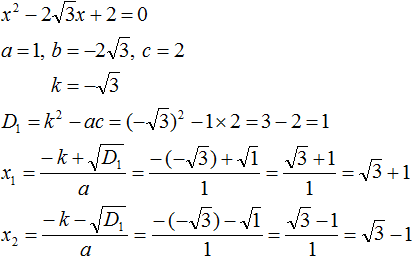
Add comment