What is a module?
Modulus is the distance from the origin to some number on the coordinate line. Since the distance is never negative, the modulus is always non-negative. Thus, the modulus of the number 3 is 3, just as the modulus of the number -3 is 3| 3 |= 3
|−3|= 3
Imagine that on the coordinate line the distance between the integers is one step. Now if you mark the numbers -3 and 3, the distance to them from the origin of coordinates will be equal to three steps: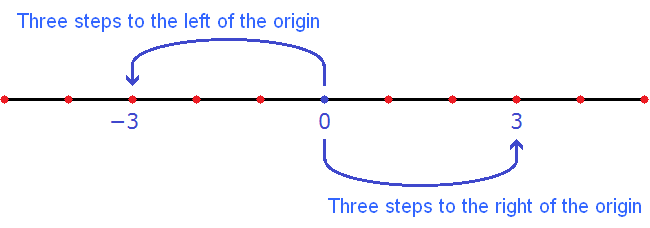
|x1 − x2|
Where x1 and x2 are numbers on the coordinate line. For example, mark the numbers 2 and 5 on the coordinate line.![]()
|2 − 5| = |−3| = 3
We see that the distance from number 2 to number 5 is three steps:

|5 − 2| = | 3 | = 3
Then we can write that |2 - 5| = |5 - 2|. In general, the following equality is true:|x1 − x2| = |x2 − x1|
This equation can be read as follows: The distance from x1 to x2 equals the distance from x2 to x1.Expansion the module
When we say that |3|= 3 or |-3|= 3 we are performing an action called modulus expansion.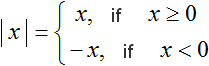
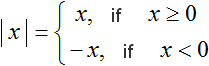
|−7|
In this case the second condition x < 0 is satisfied, because -7 < 0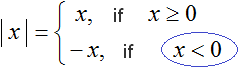
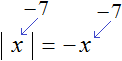
![]()
Example 2. Let x = 5. That is, we consider the modulus of the number 5
| 5 |
In this case, the first condition x ≥ 0 is satisfied, because 5 ≥ 0
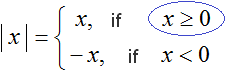
So we use the first formula. Namely | x | = x. We get | 5 | = 5.
Zero is a kind of transition point at which the module changes its order of expansion and then retains its sign. Visually, this can be represented as follows:
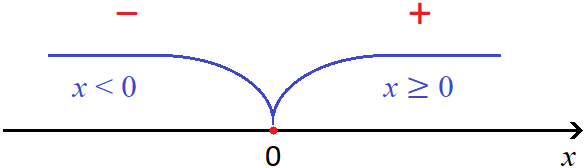
In the figure, the red minus and plus signs indicate how the module |x| will unfold at intervals x < 0 and x ≥ 0.
For example, if you take the numbers 1, 9, and 13, and they belong to the interval x ≥ 0, then according to the figure the module |x| will unfold with a plus sign:
| 1 | = 1
| 9 | = 9
| 13 | = 13
And if we take numbers smaller than zero, for example -3, -9, -15, then according to the figure the module will expand with a minus sign:
|−3| = −(−3) = 3
|−9| = −(−9) = 9
|−15| = −(−15) = 15
Example 3. Let x = √4 - 6. That is, we consider the modulus of the expression √4 - 6,
|√4 − 6|
The root of number 4 is 2. Then the modulus will be
|√4 − 6| = |2 − 6| = |−4|
x which was equal to √4-6 is now equal to -4. In this case the second condition x < 0 is satisfied, because -4 < 0
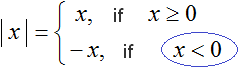
Hence, we use the second formula |x| = -x. We continue the solution in the original example:
|√4 − 6| = |2 − 6| = |−4| = −(−4) = 4
In practice, they usually reason like this:
"A module expands with a plus sign if the submodular expression is greater than or equal to zero; a module expands with a minus sign if the submodular expression is less than zero."
Examples:
|2| = 2 - the modulus opened with a plus sign because 2 ≥ 0
|-4| = -(-4) = 4 - the module opened with a minus sign, because -4 < 0
In some textbooks you can find the following notation of the modulus disclosure rule:
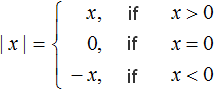
In this entry, the first condition, which previously looked like x ≥ 0, is described in more detail, namely that if x > 0, then the expression |x| will equal x, and if x=0, then the expression |x| will equal zero.
Example 4. Let x = 0. That is, we consider a modulus of zero:
| 0 |
In this case the condition x=0 is fulfilled, because 0 = 0
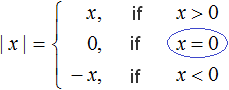
Hence: |0| = 0
Example 5. Expand the modulus in the expression |x|+ 3
If x ≥ 0, then the modulus will expand with a plus sign, and then the original expression will look like x + 3.
If x < 0, then the modulus is expanded with a minus sign, and then the original expression is -x + 3. To make this expression more readable, swap the terms, we obtain 3 - x
Now let's write down the solution this way:
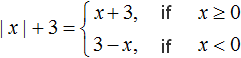
Let us check this solution for arbitrary values of x.
Suppose we need to find the value of the expression |x|+ 3 when x = 5. Since 5 ≥ 0, the modulus contained in the expression |x|+ 3 will unfold with a plus sign and then the solution will take the form:
|x|+ 3 = x + 3 = 5 + 3 = 8
Find the value of the expression |x|+ 3 when x = -6. Since -6 < 0, the modulus contained in the expression |x|+ 3 will decompose with a minus sign and then the solution will take the form:
|x| + 3 = 3 − x = 3 − (−6) = 9
Example 6. Expand the modulus in the expression x +|x + 3|
If x + 3 ≥ 0, then the modulus |x + 3| expands with a plus sign and then the original expression takes the form x + x + 3, hence 2x + 3.
If x + 3 < 0, then the module |x + 3| expands with a minus sign and then the original expression takes the form x - (x + 3), where x - x - 3 = -3.
Let's write the solution this way:
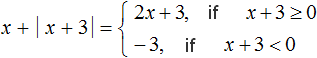
Note that the conditions x + 3 ≥ 0 and x + 3 < 0 are inequalities. They can be reduced to a simpler form by solving them:
![]()
Then the conditions from the solution can be replaced by the equivalent conditions x ≥ -3 and x < -3
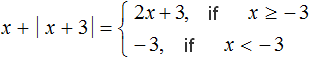
In the second case, when x is strictly less than -3, the expression x +|x + 3| will always be a constant number -3.
For example, find the value of the expression x +|x + 3| when x = -5. Since -5 < -3, according to our solution the value of expression x +|x + 3| will be -3
When x = -5,
x +|x + 3| = x − x − 3 = −5 − (−5) − 3 = −3
Find the value of the expression x +|x + 3| when x = 4. Since 4 ≥ -3, according to our solution the modulus of expression x +|x + 3| is expanded with a plus sign, and then the original expression takes the form 2x+3, where by substituting 4 we obtain 11
When x = 4,
x +|x + 3| = 2x+3 = 2 × 4 + 3 = 8 + 3 = 11
Find the value of the expression x +|x + 3| at x=-3.
Since -3 ≥ -3, according to our solution, the modulus of the expression x +|x + 3| is expanded with a plus sign, and then the original expression takes the form 2x+3, where by substituting -3 we obtain -3
x +|x + 3| = 2x + 3 = 2 × (−3) + 3 = −6 + 3 = −3
Example 3. Expand the module in expression ![]()
As before, we use the module disclosure rule:
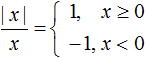
But this solution will not be correct because in the first case the condition x ≥ 0 is written, which admits that when x = 0 the denominator of expression ![]() turns to zero, and you cannot divide by zero.
turns to zero, and you cannot divide by zero.
In this example, it is more convenient to use a detailed notation of the modulus disclosure rule, where the case in which x = 0 is considered separately
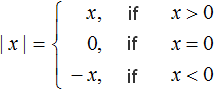
Let's rewrite the solution this way:
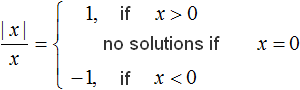
In the first case, the condition x > 0. Then expression ![]() becomes 1. For example, if x = 3, then the numerator and denominator equals 3, which results in 1
becomes 1. For example, if x = 3, then the numerator and denominator equals 3, which results in 1
![]()
And so it will be for any x greater than zero.
In the second case the condition x = 0 is written. Then there will be no solutions, because you cannot divide by zero.
In the third case, the condition x < 0 is written. Then expression ![]() becomes -1. For example, if x = -4, then the numerator becomes 4 and the denominator becomes -4, from which we get one -1
becomes -1. For example, if x = -4, then the numerator becomes 4 and the denominator becomes -4, from which we get one -1
![]()
Example 4. Expand the module in expression ![]()
If x ≥ 0, then the modulus contained in the numerator will expand with a plus sign, and then the original expression will take the form ![]() , which for any x greater than zero will be equal to one:
, which for any x greater than zero will be equal to one:
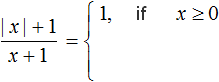
If x < 0, then the modulus expands with a minus sign, and then the original expression takes the form ![]()
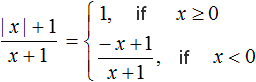
But we must keep in mind that at x = - 1 the denominator of expression ![]() turns to zero. Therefore the second condition x < 0 should be supplemented with a note about what values x can take
turns to zero. Therefore the second condition x < 0 should be supplemented with a note about what values x can take
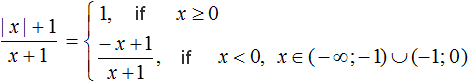
Conversion of expressions with modules
A module included in an expression can be treated as a full-fledged multiplier. It can be reduced and taken out of brackets. If a modulus is part of a polynomial, it can be added to a similar modulus.
Like an ordinary letter multiplier, a modulus has its own coefficient. For example, the coefficient of a module |x| is 1, and the coefficient of a module -|x| is -1. The coefficient of the module 3|x+1| is 3, and the coefficient of the module -3|x+1| is -3.
Example 1. Simplify the expression |x| + 2|x| - 2x + 5y and reveal the modulus in the resulting expression.
Solution
The expressions|x| and 2|x| are similar terms. Let us add them. Leave the rest unchanged:
![]()
Expand the modulus in the resulting expression. If x ≥ 0, then we get 3x - 2x + 5y, where x + 5y.
If x < 0, then we get -3x - 2x + 5y, whence -5x + 5y. We remove the factor -5 from the parentheses and obtain -5(x - y)
As a result, we have the following solution:
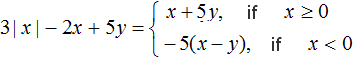
Example 2. Expand the modulus in the expression: -|x|
Solution
In this case there is a minus in front of the modulo sign. It can be understood as the minus one in front of the modulus sign. If x ≥ 0, then the modulus will expand with the plus sign, and then the original expression will look like -x
If x < 0, then the modulus expands with a minus sign, and then the original expression takes the form -(-x) where we get just x
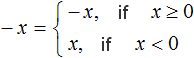
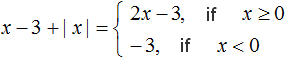
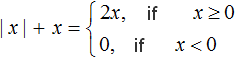
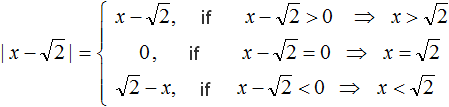
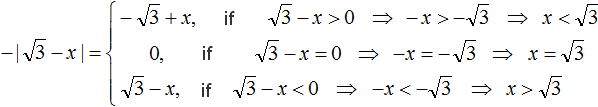
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.