When we write mixed numbers without a denominator, we convert them to decimals. When converting regular fractions into decimals, there are a few things we need to know, which we will talk about in a moment.
After the whole part is written, be sure to count the number of zeros in the denominator of the fractional part, because the number of zeros in the fractional part and the number of digits after the decimal point in the decimal must be the same. What does this mean? Consider the following example: Convert the mixed number 
into a decimal.
First write down the whole part and put a dot:
3.
And you could immediately write down the numerator of the fractional part and the decimal is ready, but you have to count how many zeros are contained in the denominator of the fractional part.
So, let's calculate the number of zeroes in the fractional part of the mixed number . We see that the denominator of the fractional part is one zero. So the decimal will have one digit after the decimal point, and this digit will be the numerator of the fractional part of the mixed number , that is, the number 2
3.2
Thus, the mixed number when converted to a decimal is converted to 3.2. This decimal is read as follows:
«Three point two-tenths»
"Tenths" because the fractional part of the mixed number contains the number 10.
Example 2. Convert the mixed number 
into a decimal.
Write down the whole part and put a dot:
5.
And we could just write the numerator of the fractional part and get a decimal 5.3, but the rule says that there must be as many digits after the decimal point as there are zeroes in the denominator of the fractional part of a mixed number . And we see that there are two zeros in the denominator of the fractional part of . So our decimal must have two digits after the decimal point, not one.
In such cases, the numerator of the fractional part should be slightly modified: add a zero before the numerator, that is, before the number 3
Now you can finish the job. Write the numerator of the fractional part after the decimal point:
5.03
We see that the number of digits after the point and the number of zeroes in the denominator of the fractional part of the mixed number are the same.
The decimal 5.03 reads like this:
«Five point three hundredths»
"Hundredths" because the denominator of the fractional part of the mixed number contains the number 100.
Example 3. Convert the mixed number 
into a decimal.
From the previous examples, we learned that to successfully convert a mixed number to a decimal, the number of digits in the numerator fractional part and the number of zeros in the denominator fractional part must be the same.
Before converting a mixed number into a decimal, its fractional part should be slightly modified, namely, to make the number of digits in the numerator fractional part and the number of zeroes in the denominator fractional part be the same.
First, we look at the number of zeros in the denominator of the fractional part. We see that there are three zeros:
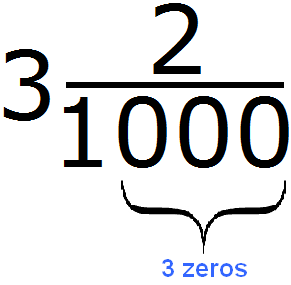
Our task is to organize three digits in the numerator of the fractional part. We already have one digit - the digit 2. We need to add two more digits. They are two zeros. We add them before number 2. As a result, the number of zeros in the denominator and the number of digits in the numerator will be the same:
Now you can do the translation of this mixed number into a decimal. First write down the whole part and put a dot:
3.
and immediately write the numerator of the fractional part
3.002
We see that the number of digits after the decimal point and the number of zeroes in the denominator of the fractional part of the mixed 
number are the same.
The decimal 3.002 reads like this:
«Three point two thousandths»
"Thousands" because the denominator of the fractional part of a mixed number contains the number 1000.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.