Repetition, Square Root
The square root of a non-negative number 
is a non-negative number whose square is equal to . This number is denoted by 
; the number is called the sub-root.
Examples:
1. 
(
, 
)
2. 
(
, 
)
Note:
, but 
– the root cannot be equal to a negative number.
– cannot be calculated. The square root of a negative number does not exist.
Function 
A function 
, where 
, is a law that maps a number to each non-negative number .
We already know the function 
. It is a function of type 
. So we will study the function on the basis of the function where 
.
The graph of a function
The graph of function is a branch of a parabola. Let us check this by making a table.
|
x |
0 |
1 |
4 |
6.25 |
9 |
|
|
0 |
1 |
2 |
2.5 |
3 |
Draw the found points on the coordinate plane (see Fig. 1).
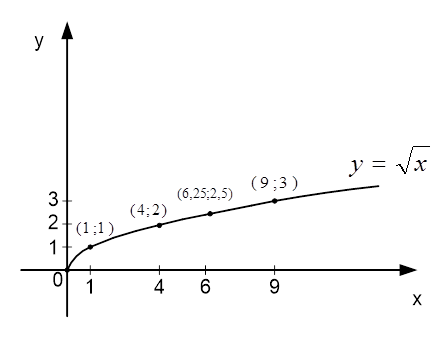
Fig. 1. The graph of the function
Let's read the graph:
If the argument increases from 0 to 
, the function increases from 0 to .
Properties of the function
1. The set of values of the function is ray 
.
Let us prove this property
The proof is
Let 
be an arbitrary number from the interval . Can we find a number such that 
? To find it, solve the equation:
The number is reached when the argument is equal to 
(see Figure 2).
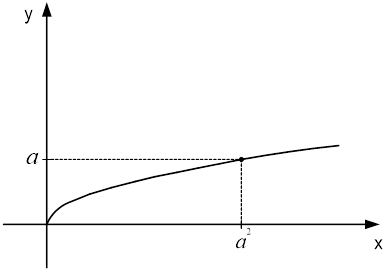
Figure 2. Illustration of the proof
Hence:
This was required to prove it.
Consequences of this property
a) The function is not bounded from above. That is, there is no largest positive number on the Y axis for this function.
b) The function is bounded from below and has the smallest value.
c) 
for all .
2. The function increases monotonically over the entire range of determination, that is, at .
Note:
A function is called monotonically increasing over the entire domain of determination if, for any 
and 
belonging to the domain of determination, the inequality 
follows from the inequality 
.
Figure 3 illustrates to us that the function is monotonically increasing.
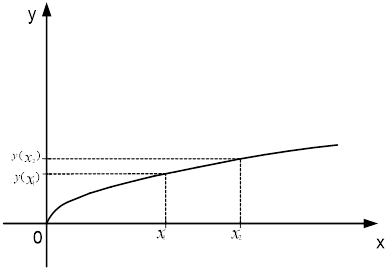
Fig. 3. Function is monotonically increasing
3. The function is convex upwards on the entire domain of definition.
For any two points, such as 
and 
(see Figure 4), the arc lying between these points will be over the segment connecting these two points, hence the function is convex upwards.
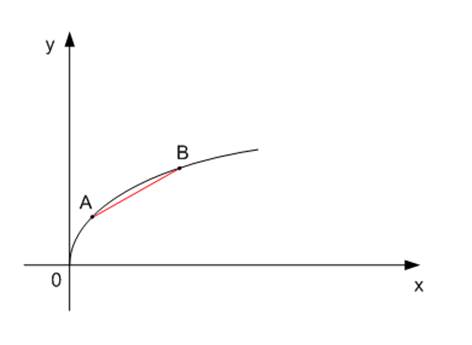
Figure 4. Function convex upwards
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.