We continue to study fractions. Today we are going to talk about comparing them. The topic is interesting and useful. It will allow the beginner to feel like a scientist in a white coat.
The point of comparing fractions is to find out which of two fractions is larger or smaller.
To answer the question which of two fractions is larger or smaller, use ratio operations such as larger (>) or smaller (<).
Mathematical scientists have already taken care of the ready-made rules that allow you to immediately answer the question of which fraction is larger and which is smaller. These rules can be safely applied.
We will look at all these rules and try to figure out why this is the case.
Comparing fractions with the same denominator
The fractions that need to be compared are different. The best case is when the fractions have the same denominators, but different numerators. In this case, the following rule applies:
Of two fractions with the same denominators, the one with the larger numerator is larger. The fraction with the smaller numerator is smaller.
For example, compare fractions 
and 
and answer which of these fractions is larger. The denominators are the same, but the numerators are different. Fraction has a larger numerator than fraction . It means that is larger than . That's how we answer. Answer with the bigger sign (>).
This example can be easily understood if you think of pizzas that are divided into four parts. A pizza is bigger than a pizza:
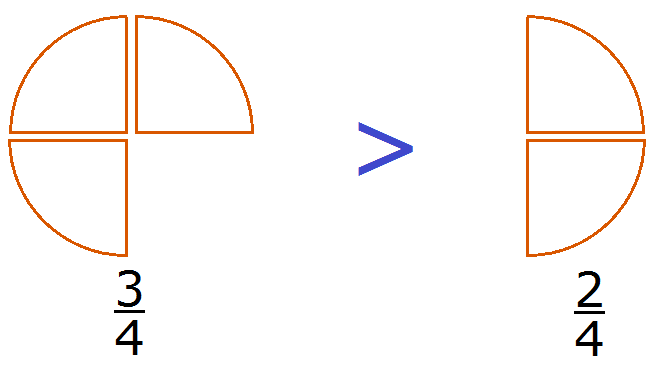
Everyone would agree that the first pizza is bigger than the second.
Comparing fractions with the same numerators
The next case we can get into is when the numerators of the fractions are the same, but the denominators are different. The following rule is provided for such cases:
If we compare two fractions with identical numerators, the one with the smaller denominator is larger. And correspondingly smaller is the fraction whose denominator is larger.
For example, compare fractions 
and 
. These fractions have the same numerators. A fraction has a smaller denominator than a fraction. So the fraction is larger than the fraction . That's how we answer: 
This example can be easily understood if you think of pizzas that are divided into three and four parts. A pizza is bigger than a pizza:
Everyone would agree that the first pizza is bigger than the second.
Comparing Fractions with Different Numerators and Different Denominators
It often happens that we have to compare fractions with different numerators and different denominators.
For example, compare fractions 
and 
. To answer the question of which of these fractions is larger or smaller, you must reduce them to the same (common) denominator. Then you can easily determine which fraction is larger or smaller.
Let's reduce fractions and to the same (common) denominator. Find the least common multiple (LCM) of the denominators of both fractions. The LCM of the denominators of fractions and is 6.
Now find the additional multipliers for each fraction. Divide the LCM by the denominator of the first fraction . LCM is 6, and the denominator of the first fraction is 2. Divide 6 by 2, and we get an additional factor 3. Write it over the first fraction:
Now find the second additional factor. Divide the LCM by the denominator of the second fraction . LCM is 6, and the denominator of the second fraction is 3. Dividing 6 by 3, we get an additional multiplier of 2. Write it over the second fraction:
Multiply the fractions by their additional multipliers:
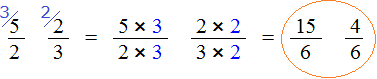
We came to the conclusion that fractions with different denominators turned into fractions with the same denominators. And we already know how to compare such fractions. Of two fractions with the same denominators, the one with the larger numerator is larger:
The rule is a rule, but we'll try to figure out why 
is bigger than 
. To do this, we highlight the whole part in the fraction . In the fraction , we don't need to isolate anything, because the fraction is proper.
After singling out the whole part of the fraction , we obtain the following expression:
After isolating the whole part in the fraction , we get the following expression:
Now it's easy to see why is bigger than . Let's draw these fractions as pizzas:
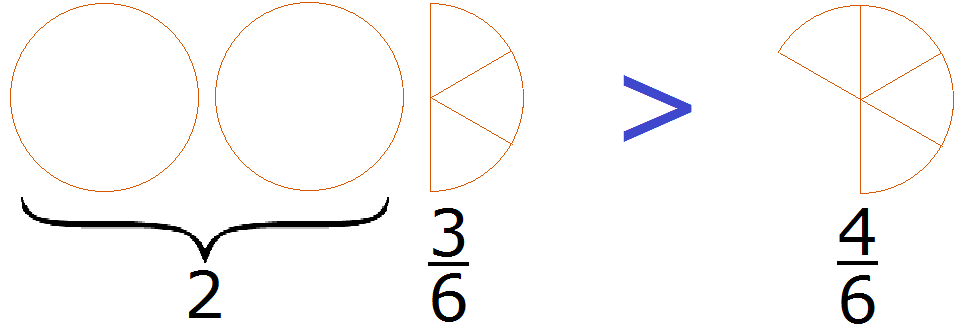
2 whole pizzas and 
pizzas, more than pizzas.
Subtraction of mixed numbers. Complex cases.
When subtracting mixed numbers, you sometimes find that things don't go as smoothly as you'd like. It often happens that when you solve an example, the answer is not what it should be.
When subtracting numbers, the subtractor must be greater than the subtractor. Only then will you get a normal answer.
For example, 10-8=2
10 - minuend
8 - subtrahend
2 - difference
The minuend 10 is greater than the subtrahend 8, so we have a normal answer of 2.
Now let's see what happens if the minuend is less than the subtrahend. Example 5-7 = -2
5 - minuend
7 - subtrahend
-2 - difference
In this case, we go beyond our usual numbers and enter the world of negative numbers, where it is too early, or even dangerous, for us to walk. To work with negative numbers, you need proper mathematical training, which we have not yet received.
If when solving subtraction examples you find that the minuend is smaller than the subtrahend, you can skip such an example for now. It is acceptable to work with negative numbers only after you have studied them.
The situation with fractions is the same. The minuend must be greater than the subtrahend. Only then will it be possible to get a normal answer. And to know if the fraction to be reduced is larger than the fraction to be subtracted, you need to be able to compare the fractions.
For example, solve example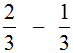
.
This is a subtraction example. To solve it, you must check to see if the fraction being minuend is greater than the fraction being subtrahend. is more than 
so we can safely go back to the example and solve it:
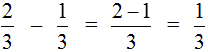
Now solve this example 
Check to see if the fraction to be minuend is larger than the fraction to be subtrahend. We find that it is smaller:
In this case, it is wise to stop and not continue with further calculations. We will return to this example when we study negative numbers.
It is also desirable to check mixed numbers before subtraction. For example, find the value of the expression 
.
First, we check to see if the minuend mixed number is greater than the subtrahend one. To do this, convert the mixed numbers into improper fractions:
We got fractions with different numerators and different denominators. To compare such fractions, we need to reduce them to the same (common) denominator. We will not describe in detail how to do it. If you have difficulties, be sure to repeat the actions with fractions.
After reducing the fractions to the same denominator, we get the following expression:
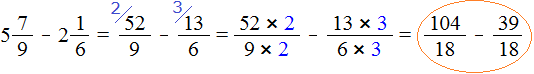
Now we need to compare fractions 
and 
. These are fractions with the same denominators. Of the two fractions with the same denominators, the fraction whose numerator is larger is larger.
The fraction has a larger numerator than the fraction . So the fraction is larger than the fraction .
This means that the subtractor 
is greater than the subtractor 
.
Which means we can go back to our example and boldly solve it:
Example 3. Find the value of the expression 
Check to see if the minuend is greater than the subtrahend.
Convert the mixed numbers into improper fractions:
We obtained fractions with different numerators and different denominators. Bring these fractions to the same (common) denominator: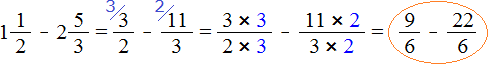
Now let's compare fractions 
and 
. The fraction has a smaller numerator than the fraction , so the fraction is smaller than the fraction
This means that the diminutive of 
is also less than the subtractor of 
This is guaranteed to lead us into the world of negative numbers. So it makes more sense to stop here and not continue calculating. We'll continue when we study negative numbers.
Example 4. Find the value of the expression 
Check to see if the minuend is greater than the subtrahend.
Convert the mixed numbers into improper fractions:
We got fractions with different numerators and different denominators. Bring them to the same (common) denominator:
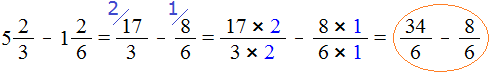
Now we need to compare fractions 
and 
. The fraction has a larger numerator than the fraction . So the fraction is larger than the fraction .
This means that the subtractor 
is greater than the subtractor 
.
Therefore, we can safely continue to calculate our example:
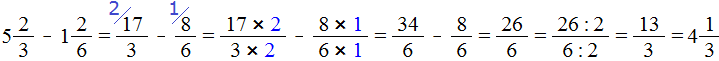
At first we got the answer 
. We reduced this fraction by 2 and got a fraction 
, but we were not satisfied with this answer either, so we separated the whole part in this answer. As a result, we got the answer 
.
Comments