What is a power in math?
A power is the product of several identical factors. For example:
2 × 2 × 2
The value of this expression is 8
2 × 2 × 2 = 8
The left part of this equation can be made shorter - first write the repeating multiplier and specify over it how many times it repeats. The repeating factor in this case is 2. It is repeated three times. So above the 2 we write the 3:
23 = 8
The expression reads "two to the third power equals eight" or "the third power of 2 equals 8".
The short form of recording multiplication of identical factors is used more often. Therefore, remember that if another number is written over some number, it is the multiplication of several identical factors.
For example, if an expression 53 is given, keep in mind that this expression is equivalent to writing 5 × 5 × 5.
The number that is repeated is called the base of the power. In expression 53, the base of the power is number 5.
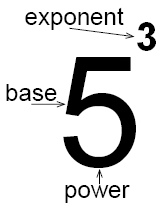
The number written above number 5 is called the exponent. In expression 53, the exponent is number 3. The exponent shows how many times the base of the power is repeated. In this case, base 5 is repeated three times
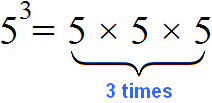
The operation of multiplying identical factors is called exponentiation.
For example, if you want to find the product of four identical factors, each of which is equal to 2, they say that the number 2 is raised to the fourth power:
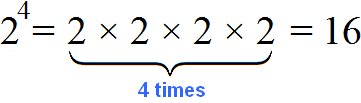
We see that the number 2 to the fourth power is number 16.
Note that in this lesson we are looking at powers with a natural exponent. This is a type of power whose exponent is a natural number. Recall that natural numbers are integers that are greater than zero. For example, 1, 2, 3, and so on.
In general, the definition of a power with a natural exponent is as follows:
The power of a with a natural exponent n is an expression of the form an, which is equal to the product of n factors, each of which is equal to a
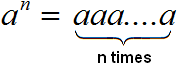
examples:
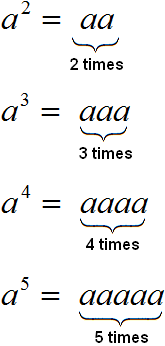
One must be careful when taking a number to the power. Often a person is inattentive and multiplies the base of a power by the exponent.
For example, the number 5 to the second power is the product of two factors, each of which is 5. This product is 25
Now suppose we inadvertently multiplied base 5 by 2.
There is an error because the number 5 to the second power is not equal to 10.
Additionally, it should be mentioned that the power of a number with exponent 1 is the number itself:
For example, the number 5 to the first power is the number 5 itself
Accordingly, if a number has no exponent, then we must assume that the exponent is equal to one.
For example, numbers 1, 2, 3 are given without exponent, so their exponents will be equal to one. Each of these numbers can be written with exponent 1
And if you exponentiate 0, you get 0. Indeed, no matter how many times nothing is multiplied by itself you get nothing. Examples:
And expression 00 has no meaning. But in some branches of mathematics, in particular analysis and set theory, expression 00 may make sense.
To practice, let's solve some examples on raising numbers to a power.
Example 1. To raise number 3 to the second power.
Number 3 to the second power is the product of two factors, each of which is equal to 3
32 = 3 × 3 = 9
Example 2. To raise the number 2 to the fourth power.
The number 2 to the fourth power is the product of four factors, each of which is 2
24 =2 × 2 × 2 × 2 = 16
Example 3. Raise number 2 to the third power.
The number 2 to the third power is the product of three factors, each of which is 2
23 =2 × 2 × 2 = 8
Powers of 10
To raise a number 10 to a power, it is enough to add after one a number of zeros equal to the exponent.
For example, let's raise the number 10 to the second power. First write down the number 10 itself and as an exponent write down the number 2
102
Now put an equal sign, write one and after this one write two zeros, because the number of zeros must be equal to the exponent
102 = 100
So the number 10 to the second power is the number 100. This is because the number 10 to the second power is the product of two factors, each of which is equal to 10
102 = 10 × 10 = 100
Example 2. Let's raise the number 10 to the third power.
In this case there will be three zeros after the one:
103 = 1000
Example 3. Let's raise the number 10 to the fourth power.
In this case there will be four zeros after the one:
104 = 10000
Example 4. Let's raise the number 10 to the first power.
In this case there will be one zero after the one:
101 = 10
Numbers 10, 100, 1000 as a power with base 10
To represent the numbers 10, 100, 1000 and 10000 as a power with base 10, you need to write the base of 10, and as the exponent specify a number equal to the number of zeros of the original number.
Let's represent the number 10 as a power with base 10. We see that it has one zero. So the number 10 as a power with base 10 will be represented as 101
10 = 101
Example 2. Let us represent the number 100 as a power of base 10. We see that number 100 contains two zeros. Therefore, the number 100 as a power with base 10 is represented as 102
100 = 102
Example 3. Let's represent the number 1,000 as a power with base 10.
1 000 = 103
Example 4. Let's represent the number 10,000 as a power with base 10.
10 000 = 104
Negative numbers and exponents
If you raise a negative number to a power, you must put it in brackets.
For example, let's raise a negative number -2 to the second power. The number -2 to the second power is the product of two factors, each of which is equal to (-2)
(−2)2 = (−2) × (−2) = 4
If we didn't bracket the number -2, we would be calculating the expression −22, which is not equal to 4. The expression -2² would be -4. To understand why, let's touch on a few points.
When we put a minus in front of a positive number, we thereby perform the operation of taking the opposite value.
Suppose a number 2 is given and we need to find its opposite number. We know that the opposite of 2 is -2. To find the opposite of 2, we just need to put minus in front of the number. Inserting a minus in front of a number is already considered a full-fledged operation in mathematics. This operation, as mentioned above, is called the operation of taking the opposite value.
In the case of expression −22 there are two operations: the operation of taking the opposite value and raising to a power. Exponentiation is a higher priority operation than taking the opposite value.
Therefore, expression −22 is calculated in two steps. First, an exponentiation operation is performed. In this case, the positive number 2 was raised to the second power
Then the opposite value was taken. This opposite value was found for the value 4. And the opposite value for 4 is -4
−22 = −4
The brackets, on the other hand, have the highest execution priority. Therefore, in the case of calculating the expression (−2)2, we first take the opposite value and then raise the negative number -2 to the second power. The result is positive 4, because the product of negative numbers is a positive number.
Example 2. Raise -2 to the third power.
-2 to the third power is the product of three factors, each of which is equal to (-2)
(−2)3 = (−2) × (−2) × (−2) = −8
Example 3. Raise -2 to the fourth power.
The number -2 to the fourth power is the product of four factors, each of which is equal to (-2)
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
It is easy to see that raising a negative number to a power can result in either a positive or a negative answer. The sign of the answer depends on the exponent of the original power.
If the exponent is even, the answer is positive. If the exponent is odd, the answer will be negative. Let's show this using the number -3 as an example
In the first and third cases, the exponent was an odd number, so the answer became negative.
In the second and fourth cases, the exponent was an even number, so the answer became positive.
Example 7. Raise the number -5 to the third power.
The number -5 to the third power is the product of three factors each equal to -5. The exponent 3 is an odd number, so we can say in advance that the answer will be negative:
(−5)3 = (−5) × (−5) × (−5) = −125
Example 8. Raise the number -4 to the fourth power.
The number -4 to the fourth power is the product of four factors, each of which is -4. The exponent of 4 is even, so we can say in advance that the answer will be positive:
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
Finding values of expressions
When finding values of expressions that do not contain brackets, the exponentiation will be performed first, followed by multiplication and division in order, and then addition and subtraction in order.
Example 9. Find the value of the expression 2 + 52
First we perform exponentiation. In this case, number 5 is raised to the second power to obtain 25. Then this result is added to the number 2
2 + 52 = 2 + 25 = 27
Example 10. Find the value of the expression −62 × (−12)
First we perform exponentiation. Note that the number -6 is not bracketed, so number 6 will be raised to the second power, and then the result will be preceded by minus:
−62 × (−12) = −36 × (−12)
Complete the example by multiplying -36 by (-12)
−62 × (−12) = −36 × (−12) = 432
Example 11. Find the value of the expression −3 × 22
First we perform exponentiation. Then the result is multiplied with the number -3
−3 × 22 = −3 × 4 = −12
If the expression contains parentheses, you must first perform the actions in those brackets, then exponentiation, then multiplication and division, and then addition and subtraction.
Example 12. Find the value of the expression (32 + 1 × 3) − 15 + 5
First perform the actions in brackets. Inside the parentheses, we apply the rules we learned earlier, i.e. first raise number 3 to the second power, then multiply 1 × 3, then add the results of raising number 3 to the power and multiplying 1 × 3. Subtraction and addition are then performed in order. Let's arrange this order of operations over the original expression:
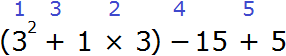
(32 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Example 13. Find the value of the expression 2 × 53 + 5 × 23
First, let's raise the numbers to a power, then perform multiplication and add up the results:
2 × 53 + 5 × 23 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Identical transformations of powers
Various identity transformations can be performed on powers, thereby simplifying them.
Suppose we need to calculate the expression (23)2. In this example, two to the third power is raised to the second power. In other words, the power is raised to another power.
(23)2 is the product of two powers, each of which is 23
Each of these powers is the product of three factors, each of which is equal to 2
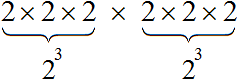
We obtain the product 2 × 2 × 2 × 2 × 2 × 2, which is 64. Then the value of the expression (23)2 or equals 64
This example can be greatly simplified. To do this, the indices of expression (23)2 can be multiplied and the product can be written over base 2
We got 26. Two to the sixth power is the product of six factors, each of which is 2. This product is 64
This property works because 23 is the product of 2 × 2 × 2, which in turn is repeated twice. Then it turns out that the base 2 is repeated six times. Hence we can write that 2 × 2 × 2 × 2 × 2 × 2 × 2 is 26
In general, for any basis a with exponent m and n, the following equality holds:
(an)m = an × m
This identity transformation is called raising the power to a power. It can be read as follows: "When raising the power to a power, the base is left unchanged and the exponents are multiplied".
After multiplying the exponents, you get another power, the value of which can be found.
Example 2. Find the value of the expression (32)2
In this example, the base is 3 and the numbers 2 and 2 are exponents. Let's use the rule of raising to a power. Leave the base unchanged, and multiply the exponents:
We got 34. And the number 3 to the fourth power is 81
Consider the rest of the transformations.
Multiplying Powers
To multiply the powers, you need to calculate each power separately, and multiply the results.
For example, multiply 22 by 33.
22 is number 4 and 33 is number 27. Multiply the numbers 4 and 27 and you get 108
22 × 33 = 4 × 27 = 108
In this example, the bases of the powers were different. In case the bases are the same, you can write one base, and as the exponent write the sum of the exponents of the original powers.
For example, multiply 22 by 23
In this example, the bases of the powers are the same. In this case we can write down one base 2 and as an exponent write the sum of exponents of powers 22 and 23, i.e. we can leave the base unchanged, and add the exponents of the original powers. It will look like this:
We got 25. The number 2 to the fifth power is 32
This property works because 22 is the product of 2 × 2, and 23 is the product of 2 × 2 × 2. Then we obtain the product of five identical factors, each of which is equal to 2. This product can be represented as 25
In general, for any a and the exponents m and n, the following equality holds:
This identity transformation is called the basic property of the power. It can be read as follows: "When multiplying powers with equal bases, the base is left unchanged and the exponents are added".
Note that this transformation can be applied to any number of powers. The main thing is that the basis is the same.
For example, find the value of the expression 21 × 22 × 23. Let's leave the base 2 unchanged, and add up the exponents:
In some tasks, it is sufficient to perform the corresponding transformation without calculating the final power. This is, of course, very convenient, since calculating large powers is not easy.
Example 1. Present the expression 58 × 25 as a power
In this task we need to make one power instead of the expression 58 × 25
The number 25 can be represented as 52. Then we get the following expression:
In this expression we can apply the main property of the power - leave the base 5 unchanged, and add the exponents 8 and 2:
The task can be considered solved because we have presented the expression 58 × 25 as one power, namely as the power of 510.
Let us write down the solution briefly:
Example 2. Present the expression 29 × 32 as a power
The number 32 can be represented as 25. Then we get the expression 29 × 25. Next, we can apply the base property of the power - leave base 2 unchanged, and add the exponents 9 and 5. The result is the following solution:
Example 3. Calculate the product 3 × 3 using the basic property of a power.
Everyone knows very well that three times three equals nine, but the task requires you to use the basic property of the power in the solution. How do we do this?
Recall that if the number is given without an exponent, then the exponent must be considered equal to one. Therefore the factors 3 and 3 can be written as 31 and 31
31 × 31
Now let's use the basic property of the power. We leave the base 3 unchanged, and add 1 and 1:
31 × 31 = 32
Then we calculate the value of the expression. The number 3 to the second power is equal to 9
31 × 31 = 32 = 9
Example 4. Calculate the product 2 × 2 × 32 × 33 using the basic property of powers.
Replace the product of 2 × 2 by 21 × 21, then by 21 + 1, and then by 22. Replace the product of 32 × 33 by 32 + 3 and then by 35
Then we calculate the value of each power and find the product:
Example 5. Perform the multiplication of x × x
These are two identical alphabetic factors with exponents of 1. For clarity, write down the exponents. Next, leave the base of x unchanged and add the exponents:
When answering a task like this at school, you should not write down the multiplication of powers with equal bases in such detail as is done here. Such calculations should be done in your head. The teacher is likely to be annoyed and give you a lower grade. Here, however, detailed notation is given so that the material will be as easy to understand as possible.
The solution to this example should preferably be written like this:
Example 6. Multiply x2 × x
The exponent of the second factor is one. Let us write it down for clarity. Next, leave the base unchanged, and add the exponents:
Example 7. Multiply y3 × y2 × y
The exponent of the third factor is one. Let us write it down for clarity. Next, leave the base unchanged, and add the exponents:
Example 8. Multiply a×a3×a2×a5
The exponent of the first factor is one. Let us write it down for clarity. Next, leave the base unchanged, and add the exponents:
Example 9. Present power 38 as a product of powers with equal bases.
In this task we have to make a product of powers whose bases will be 3 and whose sum of exponents will be 8. Any exponent can be used. Let us represent power 38 as a product of powers 35 and 33
In this example we again relied on the basic property of the power. After all, the expression 35 × 33 can be written as 35 + 3, hence 38.
Of course, it was possible to represent power 38 as a product of other powers. For example, as 37 × 31, since this product also equals 38
Representing a power as a product of powers with identical bases is mostly creative work. So you don't have to be afraid to experiment.
Example 10. Represent the power of x12 as different products of powers with bases x.
Let us use the basic property of power. Let's represent x12 as products with bases x, and sum of exponents equal to 12
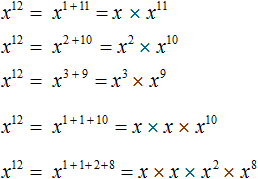
The constructions with the sums of the exponents were written for clarity. Most often they can be omitted. Then you get a compact solution:
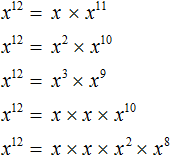
Power of a Product
In order to raise a product to a power, you must raise each factor of that product to a specified power and multiply the results.
For example, raise to the second power the product 2 × 3. Put this product in brackets and give 2 as the exponent
Now raise each factor of the product 2 × 3 to the second power and multiply the results:
The way this rule works is based on the definition of power, which was given at the beginning.
To raise the product 2 × 3 to the second power is to repeat the product twice. And if you repeat it twice, you can get the following:
2 × 3 × 2 × 3
The product does not change from rearranging the places of the factors. This allows you to group the same factors together:
2 × 2 × 3 × 3
Repeating factors can be replaced by short entries - bases with exponents. The product 2 × 2 can be replaced by 22, and the product 3 × 3 can be replaced by 32. Then the expression 2 × 2 × 3 × 3 turns into 22 × 32.
Let ab be the original product. To raise this product to power n, we must separately raise the factors a and b to the specified power n
This property holds for any number of factors. The following expressions are also valid:
Example 2. Find the value of the expression (2 × 3 × 4)2
In this example, the product 2 × 3 × 4 must be raised to the second power. To do this, take each factor of the product to the second power and multiply the results:
Example 3. To raise the product a × b × c to the third power
Put this product in brackets, and as an exponent we give the number 3
Next, raise each factor of the product to the third power:
example 4. Raise to the third power the product 3 × x × y × z
Let's bracket this product, and as an exponent let's specify 3
(3 × x × y × z)3
Let us raise each factor of the product to the third power:
(3 × x × y × z)3 = 33x3y3z3
The number 3 to the third power is 27. Let's leave the rest unchanged:
(3xyz)3 = 33x3y3z3 = 27x3y3z3
In some examples, multiplication of powers with equal exponent can be replaced by the product of bases with one exponent.
For example, calculate the value of the expression 52 × 32. Raise each number to the second power and multiply the results:
52 × 32 = 25 × 9 = 225
But it is not necessary to calculate each power separately. Instead, the given product of powers can be replaced by a product with one exponent (5 × 3)2. Then calculate the value in brackets and raise the result to the second power:
52 × 32 = (5 × 3)2 = (15)2 = 225
In this case again the rule of exponentiation of the product was used. If (a × b)n = an × bn, then an × bn = (a × b)n. That is, the left and right parts of the equality have swapped places.
Power of a Power Rule (Exponents)
We considered this transformation as an example when we tried to understand the essence of identical power transformations.
The base is left unchanged and the exponents are multiplied when the power is raised to a power:
(an)m = an × m
For example, the expression (23)2 is an increase to power - two to the third power is raised to the second power. To find the value of this expression, the base can be left unchanged, and the exponents multiplied:
(23)2 = 23 × 2 = 26
Then calculate the power of 26, which is 64
(23)2 = 23 × 2 = 26 = 64
This rule is based on the previous rules: exponentiation of the product and the main property of the power.
Let us return to the expression (23)2. The expression in brackets 23 is the product of three identical factors, each equal to 2. Then in expression (23)2 the power inside the brackets can be replaced by the product 2 × 2 × 2.
(2 × 2 × 2)2
And this is the exponentiation of the product that we studied earlier. Recall that to exponentiate a product, each factor of the product must be multiplied to the specified power and the results multiplied:
(2 × 2 × 2)2 = 22 × 22 × 22
Now we are dealing with the main property of the power. We leave the base unchanged, and add the exponents:
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26
As before we got 26. The value of this power is 64
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26 = 64
A product whose factors are also powers can also be raised to a power.
For example, find the value of the expression (22 × 32)3. Here, the exponents of each factor must be multiplied by the total exponent of 3. Then find the value of each power and calculate the product:
(22 × 32)3 = 22×3 × 32×3 = 26 × 36 = 64 × 729 = 46656
The same thing happens when you raise a product to the power of a product. We said that in the power of a product, each factor of that product is raised to a specified power.
For example, to raise the product 2 × 4 to the third power, you must write the following expression:
But earlier it was said that if a number is given without an exponent, then the exponent should be considered equal to one. It turns out that the factors of the product 2 × 4 originally have exponent equal to 1. It means that the expression 21 × 41 was raised to the third power. This is power of a power.
Let's rewrite the solution using the rule of power of a power. We should get the same result:
Example 2. Find the value of the expression (33)2
We leave the base unchanged, and multiply the exponents:
We got 36. The number 3 to the sixth power is 729
Example 3. Perform exponentiation of the expression (xy)³
Let's raise each factor of the product to the third power:
Example 4. Perform exponentiation of the expression (abc)⁵
Let's raise each factor of the product to the fifth power:
Example 5. Perform exponentiation of the expression (−2ax)3
Let's raise each factor of the product to the third power:
Since the negative number -2 was raised to the third power, it was bracketed.
Next you need to calculate what is being calculated. In this case you can calculate (−2)3 to get -8. The letter part will remain unchanged:
Example 6. Perform exponentiation of the expression (10xy)2
Example 7. Perform exponentiation of the expression (−5x)3
Example 8. Perform exponentiation of the expression (−3y)4
Example 9. Perform exponentiation of the expression (−2abx)⁴
Example 10. Simplify the expression x5 × (x2)3
Let's leave the power of x5 unchanged for now, and in the expression (x2)3 let's raise the power to a power:
x5 × (x2)3 = x5 × x2 × 3 = x5 × x6
Now let's multiply x5× x6. To do this, use the basic property of the power - leave the base of x unchanged, and add the exponents:
x5 × (x2)3 = x5 × x2× 3 = x5 × x6 = x5 + 6 = x11
Example 11. Find the value of the expression 43 × 22 using the main property of the power.
The basic property of powers can be used if the bases of the original powers are the same. In this example, the bases are different, so first we have to modify the original expression a bit, namely, to make the bases of the powers to be the same.
Let's take a close look at the power of 43. The base of this power is number 4, which can be represented as 22. Then the original expression will look like (22)3 × 22. If we raise the power of (22)3 to a power, we obtain 26. Then the original expression will take the form 26 × 22, which can be calculated using the main property of the power.
Let us write down the solution of this example:
Dividing Power
To do division of powers, you need to find the value of each power, then do division of prime numbers.
For example, divide 43 by 22.
Calculate 43, we get 64. Calculate 22, we get 4. Now divide 64 by 4, we get 16
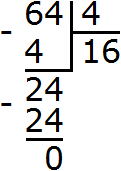
If the bases are the same when dividing the powers, the base can be left unchanged, and the exponent of the divisor can be subtracted from the exponent of the dividend.
For example, find the value of the expression 23 : 22
Let's leave the base 2 unchanged, and subtract the exponent of the divisor from the exponent of the dividend:
So the value of the expression 23 : 22 is 2.
This property is based on the multiplication of powers with equal bases, or as we used to say, on the basic property of the power.
Let's go back to the previous example 23 : 22. Here the dividend is 23 and the divisor is 22.
To divide one number by another means to find a number that, when multiplied by the divisor, yields a resulting dividend.
In our case, to divide 23 by 22 is to find a power that, when multiplied by the divisor of 22, results in 23. And what power can be multiplied by 22 to get 23 ? Obviously, only the power of21. From the basic property of powers we have:
To make sure that the value of 23 : 22 is 21, we can directly calculate the expression 23 : 22. To do this, first find the value of the power of 23, we get 8. Then we find the value of the power of 22, we get 4. Divide 8 by 4 to get 2 or 21, because 2 = 21.
23 : 22 = 8 : 4 = 2
Thus, when dividing powers with equal bases, the following equality is satisfied:
It may also happen that not only the bases are the same, but also the exponents. In this case the answer will be one.
For example, find the value of the expression 22 : 22. Calculate the value of each power and divide the resulting numbers:
When solving example 22 : 22, you can also apply the rule of division of powers with equal bases. The result is a number to the power of zero, because the difference between the exponents of powers 22 and 22 is zero:
In mathematics, it is accepted that any number to the power of zero is one:
We found out above why the number 2 to the power of zero equals one. If you calculate 22 : 22 by the usual method, without using the rule of division of powers, you will get one.
Example 2. Find the value of the expression 412 : 410
Use the rule of division of powers. Let's leave the base 4 unchanged, and subtract the exponent of the divisor from the exponent of the dividend:
412 : 410 = 412 − 10 = 42 = 16
Example 3. Present the quotient x3 : x as a power with base x
Use the rule of division of powers. We leave the base of x unchanged, and subtract the exponent of the divisor from the exponent of the dividend. The exponent of the divisor is one. For clarity, write it down:
Example 4. Present the quotient x3 : x2 as a power with base x
Let us use the rule of division of powers. Let's leave the base of x unchanged, and subtract the exponent of the divisor from the exponent of the dividend:
The division of powers can be written as a fraction. Thus, the previous example can be written as follows:
The numerator and denominator of a fraction 
may be written in expanded form, namely, as products of identical factors. The power of x3 can be written as x × x × x, and the power of x2 as x × x. Then the construction x3 − 2 can be skipped and the fraction can be shortened. The numerator and denominator can be reduced by two x factors each. The result will be one factor x
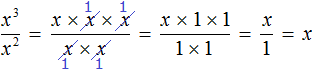
Or even shorter:
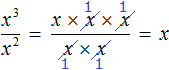
Also, it is useful to be able to quickly reduce fractions consisting of powers. For example, a fraction can be reduced by x2. To reduce by x2, divide the numerator and denominator of by x2
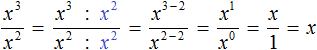
The division of powers may not be described in detail. The given reduction can be made shorter:
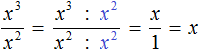
Or even shorter:
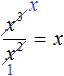
Example 5. Perform division x12 : x3
Let us use the rule of division of powers. Let's leave the base of x unchanged, and subtract the exponent of the divisor from the exponent of the dividend:
Write down the solution using fraction reduction. Let us write the division of powers x12 : x3 as 
. Then let us reduce this fraction by x3.
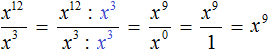
Example 6. Find the value of the expression 
In the numerator, multiply powers with equal bases:
Now apply the rule of division of powers with equal bases. We leave the base 7 unchanged, and subtract the exponent of the divisor from the exponent of the dividend:
Complete the example by calculating the power of 72
Example 7. Find the value of the expression 
In the numerator, raise the power to a power. Do this with expression (23)4
Now do the multiplication of powers with equal bases in the numerator:
Now apply the rule of division of powers with equal bases:
So the value of expression is 16
In some examples, it is possible to reduce the same factors in the course of the solution. This simplifies the expression and the calculation as a whole.
For example, find the value of expression 
. Let us write the power of 43 as the power of (22)3. Then we obtain the following expression:
In the numerator, perform the exponentiation of the power. Do this with expression (22)3
The numerator and denominator of the resulting expression contain the power 26, which can be reduced by 26
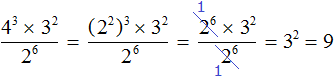
We see that this leaves us with the only power of 32, the value of which is 9.
Example 8. Find the value of the expression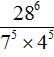 
The denominator is the product of powers with the same exponent. According to the rule of exponentiation of the product, the construction 75 × 45 can be represented as a power with one exponent (7 × 4)5. Next, multiply the expression in brackets to get 285. As a result, the original expression will take the following form:
Now you can apply the rule of division of powers:
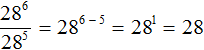
So, the value of expression 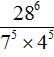is 28. Let's write down the solution in full:
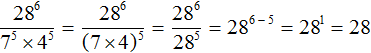
Exponents of Fractions
To raise a fraction to a power, you must raise the numerator and denominator of the fraction to a specified power.
For example, raise fraction 
to the second power. Put this fraction in brackets and give 2 as the exponent
If we do not bracket the whole fraction, it is equivalent to raising only the numerator of the fraction. If we want to raise the fraction to the second power, we should not write it as 
.
So, to calculate the value of expression , you need to raise the numerator and denominator of this fraction to the second power:
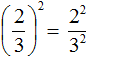
We obtained a fraction with powers in the numerator and denominator. Calculate each power separately
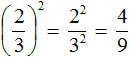
So the fraction to the second power is equal to the fraction 
.
The above rule works as follows. The fraction to the second power is the product of two fractions, each of which is equal to
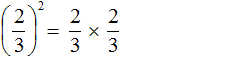
We remember that to multiply fractions, you must multiply their numerators and denominators:
And since the numerator and denominator are multiplied by the same factors, the expressions 2 × 2 and 3 × 3 can be replaced by 22 and 32, respectively:
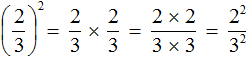
From which you get the answer .
In general, for any a and b ≠ 0 the following equality holds:
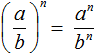
This identity transformation is called exponentiation of a fraction.
Example 2. To raise fraction 
to the third power
We conclude this fraction in brackets and give number 3 as the exponent. Then raise the numerator and denominator of the fraction to the third power and calculate the resulting fraction:
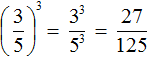
A negative fraction is raised to a power in the same way, but before calculating you should decide what sign the answer will have. If the exponent is even, the answer will be positive. If the exponent is odd, the answer will be negative.
For example, raise fraction 
to the second power:
The exponent is an even number. So the answer will be positive. Then we apply the rule of raising a fraction to a power and calculate the resulting fraction:
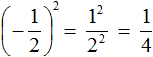
The answer is positive because is the product of two factors, each equal to a fraction of
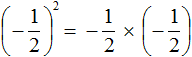
And the product of negative numbers (including rational numbers) is a positive number:
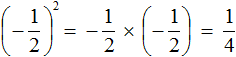
If the fraction is raised to the third power, the answer will be negative, because in this case the exponent will be an odd number. The rule of exponentiation remains the same, but before performing this exponentiation, we will need to put a minus:
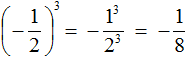
Here the answer is negative because expression 
is the product of three factors, each of which is a fraction of .
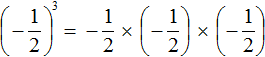
First we multiplied and and got 
, but then we multiplied by and got a negative answer of 
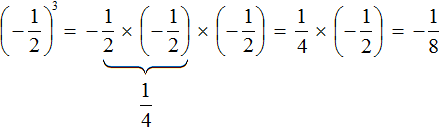
Example 3. Find the value of the expression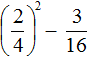 
Let's perform exponentiation of fractions:
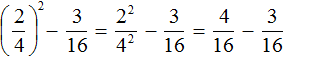
Then we calculate the value of the resulting expression:
Exponents of Decimals
When you raise a decimal to the power, you must put it in brackets. For example, let's raise a decimal 1.5 to the second power
It is allowed to convert a decimal to a fraction and to exponentiate that fraction. Solve the previous example by converting a decimal to a fraction:
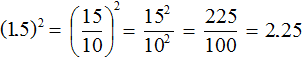
Example 2. Find the value of the power of (−1.5)3
The exponent is an odd number. So the answer will be negative
Example 3. Find the value of the power of (−2.4)2
The exponent is an even number. So the answer will be positive:
Tasks for independent decision
as a power and find the value of the power when x = 3 and n = 2.
by c¹.
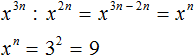
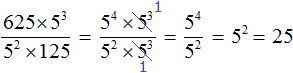
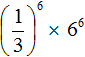
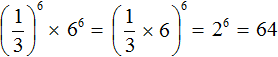
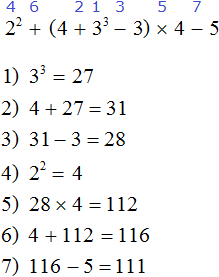
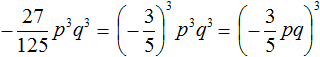
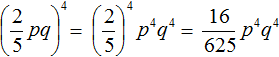
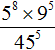
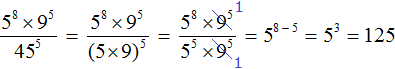
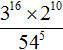
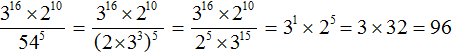
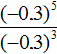
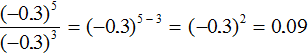
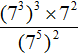
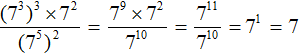
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.