We continue to deal with the basics of algebra. Today we will work with the distributive law of multiplication, namely we will consider taking out common factors.
The basic principle
The distributive law of multiplication allows you to multiply a number by a sum (or a sum by a number). For example, to find the value of the expression 3 × (4 + 5), you can multiply the number 3 by each summand in parentheses and add up the results:
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
The number 3 and the expression in parentheses can be interchanged (this follows from the commutative law of multiplication). Then each summand in parentheses will be multiplied by the number 3
(4 + 5) × 3 = 4 × 3 + 5 × 3= 12 + 15
For now we will not calculate the construction 3 × 4 + 3 × 5 and add the results 12 and 15. Let us leave the expression as 3(4 + 5) = 3 × 4 + 3 × 5. Below we will need it exactly in this form in order to understand the essence of putting the common factor behind the parentheses.
The distributive law of multiplication is sometimes called putting the multiplier inside the parentheses. In the expression 3 × (4 + 5), multiplier 3 was outside the parentheses. By multiplying it by each summand in parentheses, we essentially put it inside the parentheses. For clarity, we can write it that way, although it is not customary to write it that way:
3 (4 + 5) = (3 × 4 + 3 × 5)
Since in the expression 3 × (4 + 5) the number 3 is multiplied by each summand in parentheses, this number is a common factor for summands 4 and 5
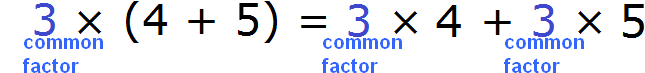
As stated earlier, by multiplying this common factor by each summand in parentheses, we bring it inside the parentheses. But the opposite process is also possible: the common factor can be put back outside the parentheses. In this case, in the expression 3 × 4 + 3 × 5 the common factor is multiplier 3. You need to take it out of the parentheses. To do this, first write down the multiplier 3
3
and the expression 3 × 4 + 3 × 5 is written next to it in parentheses, but without the common factor 3 because it was taken out of the parentheses
3(4 + 5)
The result of taking the common factor out of the parentheses is the expression 3(4 + 5). This expression is identical to the previous expression 3 × 4 + 3 × 5
3(4 + 5) = 3 × 4 + 3 × 5
If we calculate both parts of the resulting equality, we obtain an identity:
3(4 + 5) = 3 × 4 + 3 × 5
27 = 27
Factorisation: taking out common factors
Putting the common factor outside the parentheses is essentially the inverse operation of putting the common factor inside the parentheses.
If, when we put the common factor inside the parentheses, we multiply that factor by each summand in the parentheses, then when we put that factor back outside the parentheses, we must divide each summand in the parentheses by that factor.
In the expression 3 × 4 + 3 × 5, discussed above, this was the case. Each summand was divided by a common factor of 3. The products 3 × 4 and 3 × 5 are summands, because if we calculate them, we get the sum 12 + 15
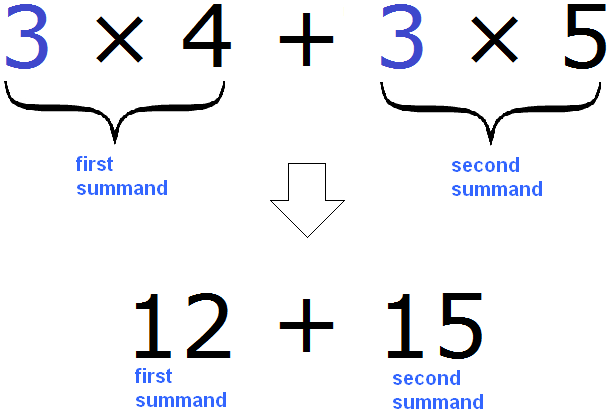
Now we can see in detail how the common factor is taken out of parentheses:
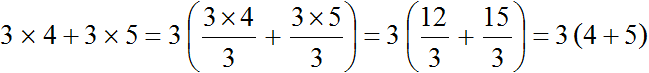
You can see that the common factor 3 is first taken out of parentheses, and then each summand is divided by this common factor in parentheses.
Dividing each summand by the common factor can be done not only by dividing the numerator by the denominator, as shown above, but also by reducing the fractions. In both cases you will get the same result:
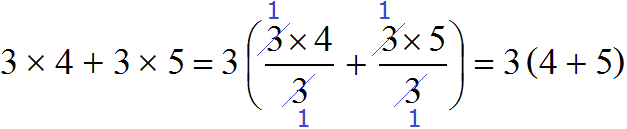
We have looked at the simplest example of putting a common factor behind parentheses to understand the basic principle.
But not everything is as simple as it seems at first glance. After a number is multiplied by each summand in parentheses, the results are added, and the common factor disappears from view.
Let's return to our example 3(4 + 5). Apply the distributive law of multiplication, that is, multiply the number 3 by each summand in parentheses and add the results:
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
Once the construction 3 × 4 + 3 × 5 is calculated, we obtain a new expression 12 + 15. We see that the common factor 3 has disappeared from view. Now, in the resulting expression 12 + 15 we will try to put the common factor back behind the parentheses, but in order to put the common factor it must first be found.
Usually in solving problems we meet such expressions in which the common factor must first be calculated before it can be taken out.
To take the common factor out of the parentheses in the expression 12 + 15, you need to find the greatest common divisor (GCD) of the summands 12 and 15. The found GCD will be the common factor.
So, let us find the GCD of the summands 12 and 15.
If you want to find GCD it is necessary to decompose the original numbers into prime factors, then write out the first expansion and remove from it the factors that are not included in the expansion of the second number. The remaining multipliers should be multiplied to get the desired GCD. If you have trouble at this point, be sure to repeat this lesson.
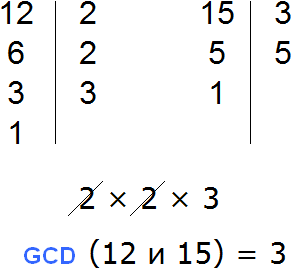
The GCD of terms 12 and 15 is 3. This number is a common factor of the summands 12 and 15. It should be taken out of parentheses. To do this, first write down the factor 3 and next to it write a new expression in parentheses, in which each summand of the expression 12 + 15 is divided by the common factor 3
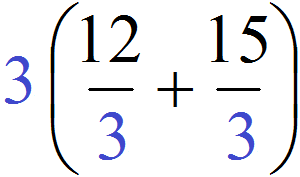
Well, the further calculation is not too difficult. The expression in parentheses is easy to calculate - twelve divided by three is four, and fifteen divided by three is five:
Thus, putting the common factor out of parentheses in the expression 12 + 15 results in the expression 3(4 + 5). The detailed solution is as follows:
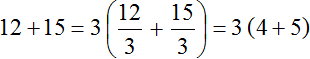
The short solution skips the entry that shows how each summand is divided by a common factor:
Example 2. Take out the common factor from the parentheses of the expression 15 + 20
The greatest common divisor of 15 and 20 is 5. This number is the common factor of the summands 15 and 20. We will take it out of the parentheses:
You have the expression 5(3 + 4).
The resulting expression 5(3 + 4) can be checked. To do this, just multiply five by each summand in parentheses. If we have done everything correctly, we should get the expression 15 + 20
Example 3. Take out the common factor in the expression 18 + 24 + 36.
Find the GCD of 18, 24 and 36. To find the GCD of several numbers, you need to decompose these numbers into prime factors, then find the product of the common factors:
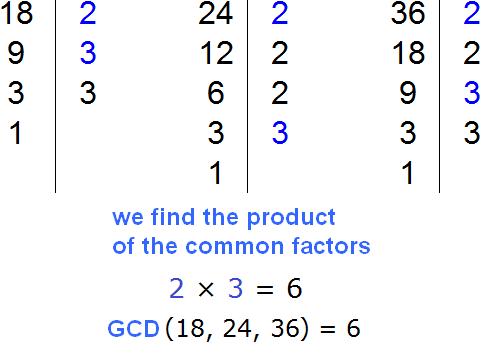
The GCD of 18, 24, and 36 is 6. This number is a common factor of 18, 24, and 36. We will take it out of the parentheses:
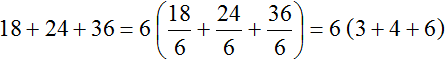
Let's check the resulting expression. To do this, multiply the number 6 by each summand in parentheses. If we have done everything correctly, we should get the expression 18 + 24 + 36
Example 4. Take out the common factor in the expression 13 + 5
The summands 13 and 5 are prime numbers. They are only decomposable by one and themselves:
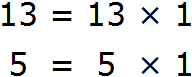
This means that the summands 13 and 5 have no common factors except one. Consequently, it makes no sense to take the unit out of the parentheses, because it will not do anything. Let us show that:
Example 5. Take out the common factor in the expression 195 + 156 + 260
Find the GCD of 195, 156, and 260
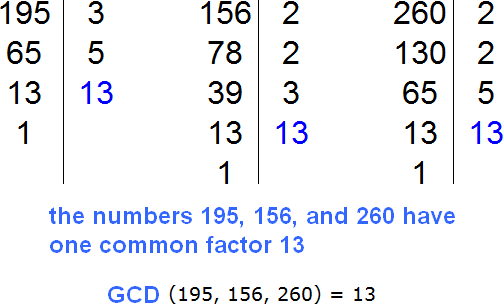
GCD of the summands 195, 156, and 260 is 13. This number is a common factor for the summands 195, 156, and 260. We put it outside the parentheses:
Let's check the resulting expression. To do this, multiply 13 by each summand in parentheses. If we have done everything correctly, we should get the expression 195 + 156 + 260
An expression in which you want to put the common factor out of parentheses can be not only the sum of numbers, but also the difference. For example, bracket the common factor in the expression 16 - 12 - 4. The greatest common divisor of 16, 12, and 4 is 4. Put this number behind the parentheses:
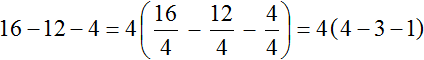
Let's check the resulting expression. To do this, multiply the four by each number in parentheses. If we have done everything correctly, we should get the expression 16 - 12 - 4
Example 6. Take out the common factor from the expression 72 + 96 - 120.
Find the GCD of 72, 96 and 120
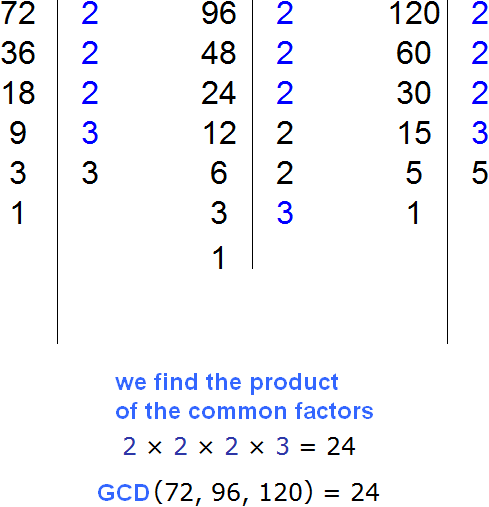
The GCD for 72, 96, and 120 is 24. This number is a common factor of the summands 195, 156, and 260. We take it out of the parentheses:
Let's check the resulting expression. To do this, multiply 24 by each number in parentheses. If we have done everything correctly, we should get the expression 72+96-120
The common factor to be put out of parentheses can also be negative. For example, put the common factor in the expression -6 - 3. There are two ways to remove the common factor from the parentheses in such an expression. Consider each of them.
Method 1.
Replace subtraction with addition:
−6 + (−3)
Now we find the common factor. The common factor of this expression is the greatest common divisor of the moduli of the summands -6 and -3.
The modulus of the first summand is 6. And the modulus of the second summand is 3. The GCD (6 and 3) is 3. This number is the common factor of the summands 6 and 3. Put it behind the parentheses:
The expression obtained this way is not very neat. Many parentheses and negative numbers do not make the expression simple. Therefore, you can use the second method, the essence of which is to take -3, not 3, out of parentheses.
Method 2.
Just like last time, replace subtraction with addition
−6 + (−3)
This time we will take -3 instead of 3 out of the parentheses
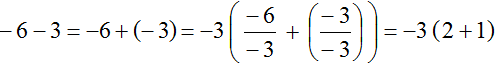
The expression obtained this time looks much simpler. Let's write down the solution briefly to make it even simpler:
Allowing the negative multiplier to be taken out of parentheses is due to the fact that the expansion of the numbers -6 and (-3) can be written in two ways: first, make the multiplier negative, and the multiplier positive:
−6 = −2 × 3
−3 = −1 × 3
in the second case, the multiplier can be made positive and the multiplier negative:
−6 = 2 × (−3)
−3 = 1 × (−3)
This means that we can take out of the parentheses whatever multiplier we want.
Example 8. Take out the common factor in the expression -20 - 16 - 2
Substitute addition for subtraction
−20 − 16 − 2 = −20 + (−16) + (−2)
The greatest common divisor of -20, -16, and -2 is 2. This number is the common factor of these summands. Let's see what it looks like:
−20 = −10 × 2
−16 = −8 × 2
−2 = −1 × 2
But the above decompositions can be replaced by identically equal decompositions. The difference will be that the common factor will not be 2, but -2
−20 = 10 × (−2)
−16 = 8 × (−2)
−2 = 1 × (−2)
Therefore, for convenience, we can put -2, not 2, behind the parentheses.
Let us write down the above solution briefly:
And if we were to take 2 out of the parentheses, we would get a not-so-tidy expression:
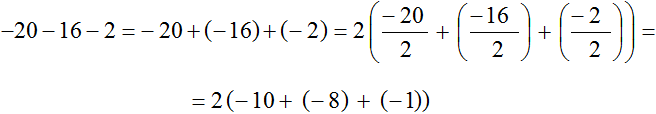
Example 9. Take out the common factor from the parentheses in the expression -30 - 36 - 42
Replace subtraction with addition:
−30 + (−36) + (−42)
The greatest common divisor of -30, -36, and -42 is 6. This number is the common factor for these summands. But we do not bracket 6, but -6, because the numbers -30, -36, and -42 can be represented this way:
−30 = 5 × (−6)
−36 = 6 × (−6)
−42 = 7 × (−6)
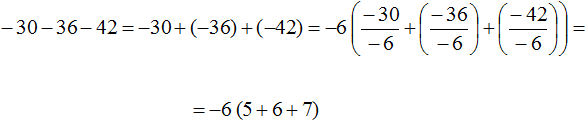
Negative sign outside of parentheses
When solving problems, it can sometimes be useful to move the negative sign outside parentheses. This simplifies the expression and makes it simpler.
Consider the following example. Take out the minus in the expression -15 + (-5) + (-3)
For clarity, let us put this expression in parentheses, because we are talking about taking the minus out of these parentheses
( −15 + (−5) + (−3) )
So, to take the minus out of the parentheses, we need to write the minus before the parentheses and write all the summands in the parentheses, but with opposite signs. We leave the signs of operations (i.e. pluses) unchanged:
−(15 + 5 + 3)
We took the minus out of the parentheses in the expression -15 + (-5) + (-3) and got -(15 + 5 + 3). Both expressions are equal to the same value -23
−15 + (−5) + (−3) = −23
−(15 + 5 + 3) = −(23) = −23
Therefore, the expressions -15 + (-5) + (-3) and -(15 + 5 + 3) can be equated, because they are equal to the same value:
−15 + (−5) + (−3) = −(15 + 5 + 3)
−23 = −23
In fact, the distributive law of multiplication is again triggered when the minus is put outside the parentheses:
a(b + c) = ab + ac
If we interchange the left and right parts of this identity, we obtain that the factor a is taken out of the parentheses
ab + ac = a(b+c)
The same thing happens when we take out the common factor in other expressions and when we take the minus out of parentheses.
Obviously, when the minus is taken out of parentheses, it is not the minus but the minus one that is taken out. Earlier we said that it is customary not to write the coefficient 1.
Therefore, minus is formed before the parentheses, and the signs of the summands that were in parentheses change their sign to the opposite, because each summand is divided by minus one.
Let's return to the previous example and see in detail how the minus was actually taken out of parentheses
Example 2. Take out a negative sign in the expression -3 + 5 + 11
Put the minus in the parentheses and write the expression -3 + 5 + 11 with the opposite sign of each summand:
−3 + 5 + 11 = −(3 − 5 − 11)
As in the last example, here we have not a minus, but a minus one, behind the parentheses. The detailed solution is as follows:
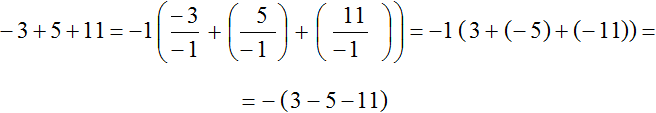
At first we got the expression -1(3 + (-5) + (-11)), but then we opened the internal parentheses and got the expression -(3 - 5 - 11). Opening parentheses is the topic of the next lesson, so if this example is difficult for you, you can skip it for now.
Factorising by taking out common factors in a variable expression
It is much more interesting to take out the common factor out of parentheses in a variable expression.
First, let us consider a simple example. Suppose we have the expression 3a + 2a. Take the common factor out of parentheses.
In this case, the common factor is clearly visible: it is the factor a. We put it out of parentheses. To do this, write down the factor a itself and write the expression 3a + 2a next to it in parentheses, but without the factor a because it was taken out of the parentheses:
As in the case of a numerical expression, each summand is divided by the taken out common factor. It looks like this:
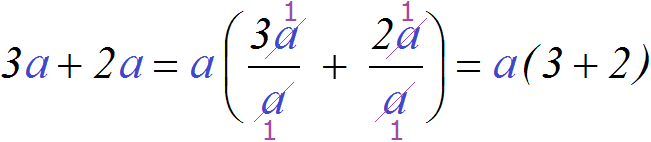
In both fractions, the variables a have been reduced by a. The numerator and the denominator are replaced by ones. The reason for the units is that any number can take the place of the variable a. This variable was located in both the numerator and the denominator. And if the same numbers are in the numerator and denominator, then the greatest common divisor for them will be that number itself.
For example, if instead of the variable a you substitute number 4, the construction 
will look like the following: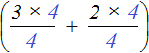 
. Then the fours in both fractions can be reduced by 4:
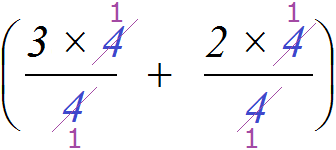
This is the same as before, when the variable a was used instead of quadruples.
So you should not be frightened when you see variable abbreviation. A variable is a full-fledged multiplier, even if expressed by a letter. Such a multiplier can be taken out of parentheses, reduced, and perform other actions that are allowed to ordinary numbers.
A variable expression contains not only numbers, but also letters (variables). Therefore, a common factor that is taken out of parentheses is often a letter factor consisting of a number and a letter (a quotient and a variable). For example, the following expressions are variable multipliers:
3a, 6b, 7ab, a, b, c
Before putting such a multiplier out of parentheses, we need to decide what number will be in the numeric part of the common factor and what variable will be in the variable part of the common factor. In other words, we need to know what factor the common factor will have and what variable will be included in it.
Consider the expression 10a + 15a. Try to put the common factor in it outside the parentheses. First, we determine what the common factor will consist of, that is, we find out its coefficient and what variable will be included in it.
The coefficient of the common factor must be the greatest common divisor of the coefficients of the letter expression 10a + 15a. The coefficients of this expression are 10 and 15, and their greatest common divisor is 5. This means that 5 is the coefficient of the common factor, which is taken out of parentheses.
Now let's determine which variable will be included in the common factor. To do this, look at the expression 10a + 15a and find the alphabetic factor that is included in all the summands. In this case, it is the factor a. This factor is included in each summand of the expression 10a + 15a. So the variable a will be included in the literal part of the common factor to be taken out of the parentheses:
Now we have to take the common factor 5a out of parentheses. To do this, divide each summand of the expression 10a + 15a by 5a. For clarity, the coefficients and numbers will be separated by the multiplication sign (×)
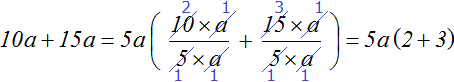
Let's check the resulting expression. To do this, multiply 5a by each summand in parentheses. If we have done everything correctly, we get the expression 10a + 15a
The variable multiplier can not always be taken out of parentheses. Sometimes the common factor consists only of a number, because there is nothing suitable for the variable part in the expression.
For example, put the common factor in the expression 2a - 2b outside the parentheses. Here the common factor will be only number 2, and there are no common factors among the variable factors in the expression. That is why in this case only multiplier 2 is taken out.
Example 2. Take out the common factor of the expression 3x + 9y + 12
The coefficients of this expression are 3, 9, and 12, their GCD is 3. So the coefficient of the common factor to be taken out of parentheses is 3. And there is no common factor among the alphabetic factors (variables). Therefore the final common factor is 3.
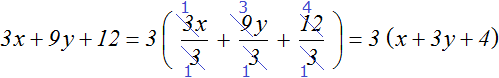
Example 3. Take out the common factor from the expression 8x + 6y + 4z + 10 + 2
The coefficients of the expression are 8, 6, 4, 10 and 2, their GCD is 2. So the coefficient of the common factor to be taken out of parentheses is 2. And there is no common factor among the alphabetic factors. Therefore the final common factor is 2.
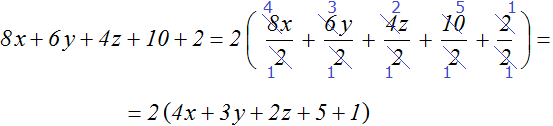
Example 4. Take out the common factor 6ab + 18ab + 3abc
The coefficients of this expression are 6, 18, and 3, their GCD is 3. So the coefficient of the common factor to be taken out of parentheses is 3. The variable part of the common factor will include the variables a and b, because in the expression 6ab + 18ab + 3abc these two variables are included in each summand. Therefore, the final common factor is 3ab
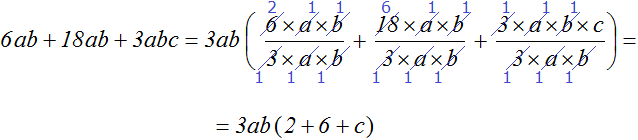
When solving the expression in detail, it becomes unwieldy and even incomprehensible. In this example this is more than noticeable. This is due to the fact that we reduce the multipliers in the numerator and denominator. It is best to do this in your head and write down the results of the division at once. Then the expression will be short and neat:
As in the case of a numeric expression in a literal expression, the common factor can also be negative.
For example, put the common factor behind the parentheses in the expression -3a - 2a.
For convenience, replace subtraction with addition
−3a − 2a = −3a + (−2a)
The common factor in this expression is the factor a. But not only a but also -a can be put outside the parentheses. We will put it out of parentheses:
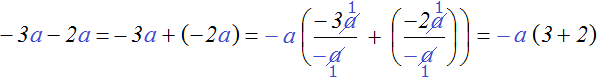
The result is a neat expression -a(3+2). We should not forget that the multiplier -a actually looked like -1a and after reduction in both fractions of variables a, there were minus ones left in the denominators. That is why we end up with positive answers in parentheses
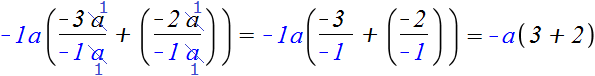
Example 6. Take out the common factor in the expression -6x - 6y
Substitute addition for subtraction
−6x−6y = −6x+(−6y)
We remove the parentheses of -6
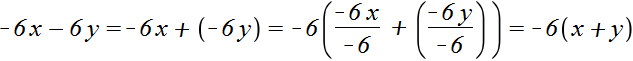
Let's write down the solution shortly:
−6x − 6y = −6(x + y)
Example 7. Parenthesize the common factor in the expression -2a - 4b - 6c
Substitute addition for subtraction
−2a-4b-6c = −2a + (−4b) + (−6c)
Let's take -2 out of the parentheses.
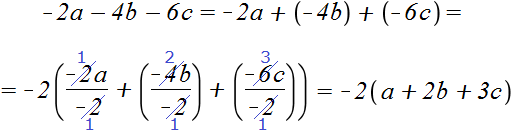
Let's write down the solution shortly:
−2a − 4b − 6c = −2(a + 2b + 3c)
Putting a common factor out of parentheses is a very important topic. This lesson covers only the basics and the simplest examples. We will come back to this topic when we study polynomials.
Be sure to study this lesson, because when you study polynomials you will need to put a complex multiplier consisting of powers behind the parentheses.
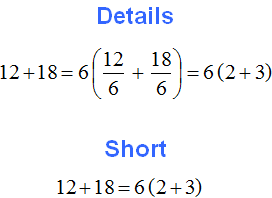
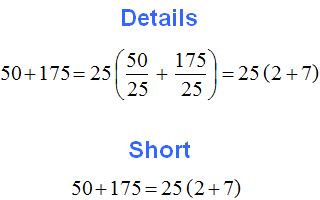
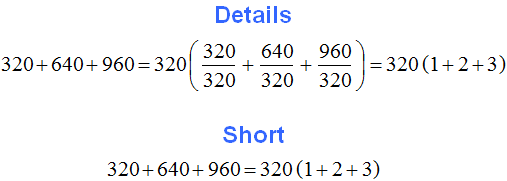
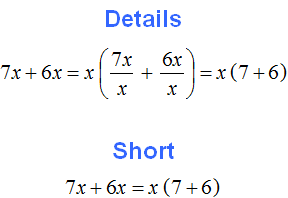
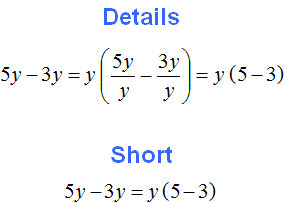
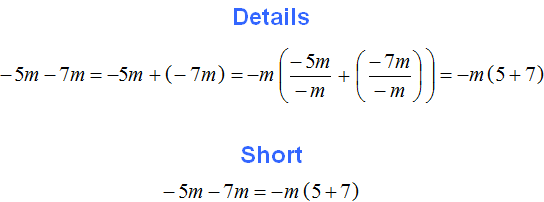
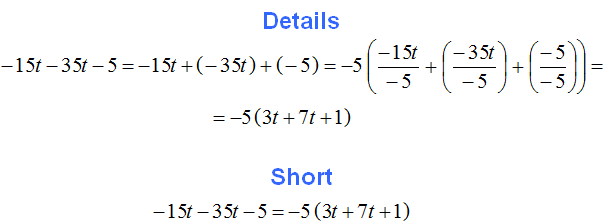
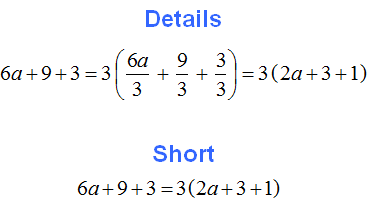
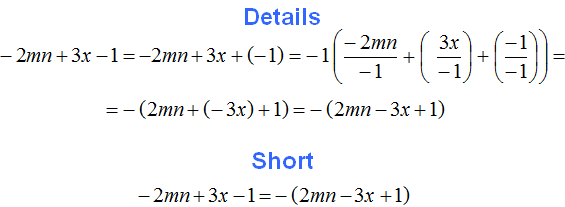
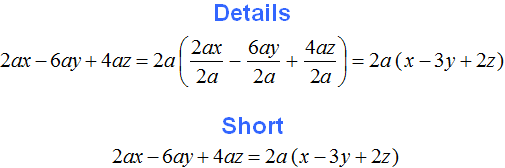
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.