Proportion

We continue to learn about ratios. In this lesson we will learn about proportion.

What is proportion?

Proportion says that two fractions (ratios) are equal. For example, a ratio of is equal to a ratio of

This proportion reads as follows:

Ten is to to five as two is to one

The fractions that make up the proportion are always equal. For example, if you divide both fractions in the proportion , you will get 2 in both parts:

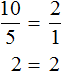
Suppose there are 10 girls and 5 boys in the class

Write down the ratio of ten girls to five boys:

10 : 5

Convert this ratio to a fraction

By doing the division in this fraction, we get 2. That is, ten girls will relate to five boys so that there will be two girls per boy

Now consider another class with two girls and one boy

Let's write down the ratio of two girls to one boy:

2 : 1

Convert this ratio to a fraction:

By doing the division in this fraction, we again get 2. That is, two girls will be so related to one boy that there will be two girls for that one boy:

We can conclude that the ratio of is proportional to the ratio of . This is why it reads "ten is to five as two is to one".

In our example, ten girls is to five boys in the same way as two girls is to one boy.

Example 2. Consider the ratio of 12 girls to 3 boys

as well as the ratio of 12 girls to 2 boys

These ratios are not proportional. In other words, we cannot write that , because the first ratio, as seen in the picture, shows that there are four girls for every boy, and the second ratio shows that there are six girls for every boy.

Therefore, the ratio of is not proportional to the ratio of .

From the examples we have considered, we can see that the proportion is made up of fractions. The first proportion we looked at, , consists of two fractions. If we do division in these fractions, we get that 2=2. It is clear that 2 equals 2.

The second proportion we considered was . We concluded that it was not composed correctly, so we put a sign not equal (≠) between the fractions and . If we perform division in these fractions, we get the numbers 4 and 6. It is clear that 4 is not equal to 6.

Consider the proportion . This proportion is correct because the ratios and are equal to each other:

You can check this by doing division in these fractions, that is, divide 4 by 2, and 8 by 4. This will result in twos on both sides. And 2 equals 2.

2 = 2

All numbers in the proportion (numerators and denominators of both fractions) are divided into two kinds: Means and Extremes.

In our proportion, the extremes are 4 and 4, and the means are 2 and 8.

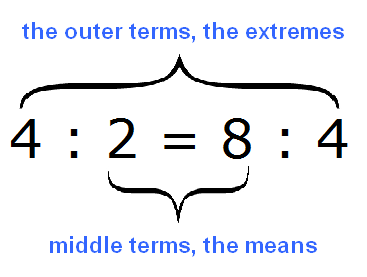
Why are the outer terms called extreme and the middle terms called means? If you write down the proportion in regular form instead of fractional form, everything becomes clear at once:

4 : 2 = 8 : 4

The numbers 4 and 4 are at the outer of fraction, so they are called extreme, and the numbers 2 and 8 are in the middle, so they are called middle:

Using variables, the proportion can be written as follows:

This expression can be read as follows:

a is to b as c is to d

The meaning of this sentence is already clear. We are talking about the terms involved in the proportion. a and d are the extreme members of the proportion, b and c are the middle members of the proportion.

The cross product property.

Cross Product Property:

The product of the extremes is equal to the product of the means..

We know that a product is nothing more than ordinary multiplication. To check if the proportion is correct, multiply its extreme and middle terms. If the product of the extreme terms equals the product of the middle terms, the proportion is correct.

For example, check if the proportion is correct. To do this, multiply its extreme and middle terms. It is easy to see that the extreme and middle terms of the proportion are located "crosswise", so there is nothing complicated about multiplication. Multiply the terms of the proportion "crosswise":

4 × 4 = 16 - the product of the extreme terms of the proportion is 16.

2 × 8 = 16 - the product of the middle terms of the proportion is also 16.

4 × 4 = 2 × 8

16 = 16

4 × 4 = 2 × 8 - the product of the extreme terms is equal to the product of the middle terms. So the proportion is correct.

Example 2. Check if the proportion of is correct

Check whether the product of the extreme terms of the proportion is equal to the product of its middle terms. Multiply the terms crosswise:

2 × 6 = 12 - the product of the extreme terms of the proportion is 12

3 × 1 = 3 - the product of the middle terms of the proportion is 3

2 × 6 ≠ 3 × 1

12 ≠ 3

2 × 6 ≠ 3 × 1 - the product of the extreme terms of the proportion is NOT equal to the product of its middle terms. So the proportion is not made correctly.

Therefore, in the proportion it is more reasonable to replace the equal sign (=) with a sign not equal (≠).

Video lesson

Add comment