You will often find an expression in which the division of fractions is written with a fractional dash. For example, the expression ![]() can be written as follows:
can be written as follows:
![]()
What is the difference between expressions ![]() and
and ![]() ? Actually, there is no difference. The two expressions have the same meaning and can be equated:
? Actually, there is no difference. The two expressions have the same meaning and can be equated:
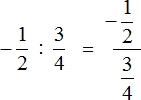
In the first case, the division sign is a colon and the expression is written on one line. In the second case, the division of fractions is written with a fractional dash. The result is a fraction, which is called a complex fraction.
When encountering such complex fractions, you must apply the same rules for dividing regular fractions. The first fraction must be multiplied by the inversed second fraction.
It is extremely inconvenient to use such fractions in the solution, so you can write them in an understandable form, using a colon instead of a fractional line as the division sign.
For example, let's write down the complex fraction ![]() in an understandable form. To do this, we first need to figure out where the first fraction is and where the second fraction is, because it is not always possible to do this correctly. Complex fractions can have several fractions that can be confusing. The main fractional line, which separates the first fraction from the second, is usually longer than the others.
in an understandable form. To do this, we first need to figure out where the first fraction is and where the second fraction is, because it is not always possible to do this correctly. Complex fractions can have several fractions that can be confusing. The main fractional line, which separates the first fraction from the second, is usually longer than the others.
After determining the main fractional line, you can easily figure out where the first fraction is and where the second fraction is:
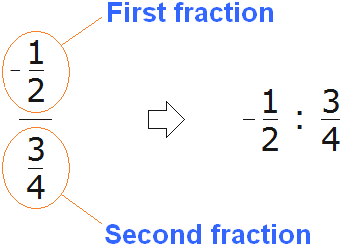
And then you can use the method of dividing fractions - multiply the first fraction by the inversed second one.
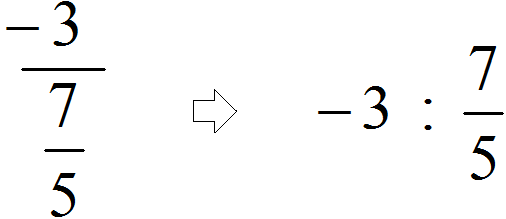
Example 2. Let's write down the complex fraction ![]() in understandable form
in understandable form
Find the main fractional line (it is the longest) and see that the integer -3 is divided by an ordinary fraction ![]() .
.
And if we mistakenly took the second fractional line as the main line (the shorter one), then it would turn out that we divide the fraction ![]() by the integer 5
by the integer 5
![]()
In this case, even if this expression is calculated correctly, the problem will not be solved correctly, because the divisor in this case is the number -3, and the divisor is the fraction ![]() .
.
Example 3. Let us write down the multi-story fraction ![]() in understandable form
in understandable form
Find the main fractional line (it is the longest) and see that the fraction ![]() is divided by the integer 2
is divided by the integer 2

And if we mistakenly took the first fractional line as the main line (the shorter one), it would turn out that we are dividing an integer -5 by a fraction ![]()
![]()
In this case, even if this expression is calculated correctly, the problem will not be solved correctly, because the divisor in this case is a fraction ![]() , and the divisor is an integer 2.
, and the divisor is an integer 2.
Despite the fact that complex fractions are awkward to work with, we will encounter them very often, especially when studying higher mathematics.
Naturally, it takes extra time and space to convert complex fractions into an understandable form. So we can use a faster method. This method is convenient and yields a ready-made expression with the first fraction multiplied by the inversed second one.
This method is implemented as follows:
If the fraction is four stories, such as ![]() , then the number on the first floor is raised to the top floor. And the digit on the second floor goes up to the third floor. The obtained digits should be connected by multiplication signs ( × )
, then the number on the first floor is raised to the top floor. And the digit on the second floor goes up to the third floor. The obtained digits should be connected by multiplication signs ( × )
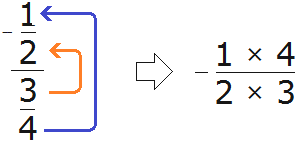
As a result, bypassing the intermediate notation ![]() , we get a new expression
, we get a new expression ![]() , in which the first fraction is already multiplied by the fraction inverse of the second. This is very convenient!
, in which the first fraction is already multiplied by the fraction inverse of the second. This is very convenient!
To avoid mistakes when using this method, you can follow the following rule:
From the first to the fourth. From the second to the third.
The rule refers to the "levels". The figure from the first "level" should be raised to the fourth "level". And the figure from the second "level" should be raised to the third "level".
Let's try to calculate the complex fraction ![]() using the above rule.
using the above rule.
So, the number on the first "level" goes up to the fourth"level", and the number on the second "level" goes up to the third "level"
As a result, bypassing the intermediate notation ![]() we get a new expression
we get a new expression ![]() , in which the first fraction is already multiplied by the fraction inverse of the second. Then we can use the available knowledge:
, in which the first fraction is already multiplied by the fraction inverse of the second. Then we can use the available knowledge:
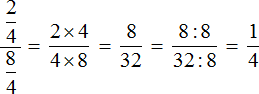
Example 4. Let's try to calculate the complex fraction ![]() using the new scheme.
using the new scheme.
There is only the first, second and fourth "level". The third "level" is missing. But we do not deviate from the basic scheme: we raise the figure from the first "level" to the fourth "level". And since the third "level" is missing, we leave the figure on the second "level" as it is
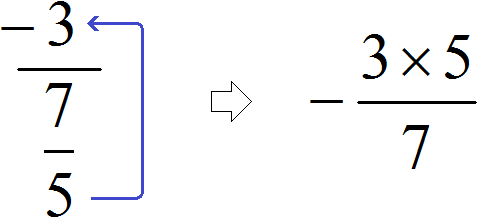
As a result, bypassing the intermediate notation ![]() we have a new expression
we have a new expression ![]() , in which the first number -3 is already multiplied by the fraction inverse of the second. Next, we can use the existing knowledge:
, in which the first number -3 is already multiplied by the fraction inverse of the second. Next, we can use the existing knowledge:

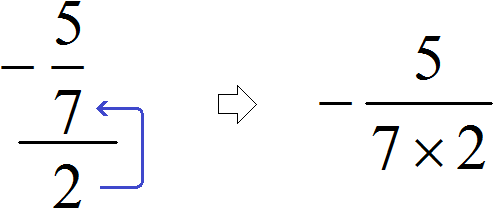
Example 5. Let's try to calculate the complex fraction ![]() using the new scheme.
using the new scheme.
There is only the second, third and fourth "level". The first "level" is missing. Since the first "level" is missing, we don't need to go up to the fourth "level", but we can raise the number from the second "level" to the third:
As a result, bypassing the intermediate notation ![]() , we have a new expression
, we have a new expression ![]() , in which the first fraction is already multiplied by the number inverse of the divisor. Next, we can use the existing knowledge:
, in which the first fraction is already multiplied by the number inverse of the divisor. Next, we can use the existing knowledge:
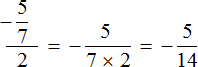
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.