Here are short articles answering one specific question.
Multiplying decimals by 0.1, 0.01 and 0.001 is done in the same way as multiplying a decimal by a decimal.
It is necessary to multiply fractions like regular numbers and put a dot in the answer, counting as many digits to the right as there are digits after the dot in both fractions.
For example, multiply 3.25 by 0.1
Multiply these fractions like regular numbers, ignoring the dots:
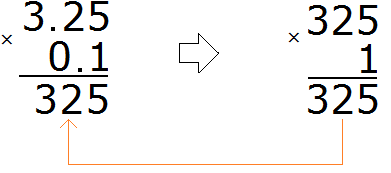
We got 325. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the point in fractions 3.25 and 0.1. There are two digits after the dot in fraction 3.25 and one digit in fraction 0.1. The total is three digits.
Go back to 325 and start moving from right to left. We need to count three digits to the right and put a dot. After counting the three digits, we find that the digits have run out. In this case we need to add one zero and put a dot:
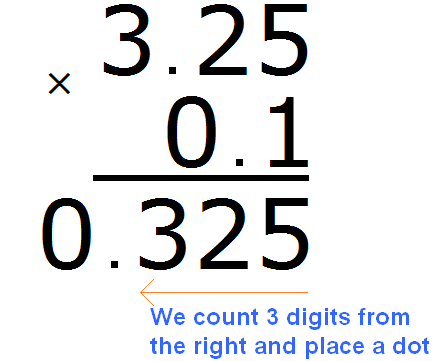
The answer is 0.325. So the value of the expression 3.25 × 0.1 is 0.325
3.25 × 0.1 = 0,325
Any whole number can be multiplied by a fraction. All you have to do is multiply the number by the numerator of the fraction.
For example, multiply the number 5 by a fraction ![]() . To solve this example, multiply the number 5 by the numerator of the fraction
. To solve this example, multiply the number 5 by the numerator of the fraction ![]()
![]()
The answer is an improper fraction. Let's separate the whole part of the fraction:
![]()
If there are five whole pizzas and we take half of that number, we have two whole pizzas and half a pizza:

There are problems that require you to multiply mixed numbers. For example, multiply ![]() and
and ![]() . To solve this example, you must convert these mixed numbers to improper fractions, then multiply the improper fractions:
. To solve this example, you must convert these mixed numbers to improper fractions, then multiply the improper fractions:
![]()
Let's try to understand this example with the help of a picture. Let's say there is one whole pizza and one half of a pizza:

To multiply a mixed number by a fraction, you must convert the mixed number to an improper fraction, then multiply the proper fractions.
Example 1. Find the value of the expression ![]()
Convert the mixed number ![]() into an improper fraction. After translation, the number will become a fraction of
into an improper fraction. After translation, the number will become a fraction of ![]() . Then we can multiply that fraction by
. Then we can multiply that fraction by ![]()
![]()
Let's say there is one whole pizza and a half pizza:
To multiply a multi-digit number by a single-digit number, multiply each digit of the multi-digit number by that single-digit number. For example, find the value of the expression 12 x 3. Write this expression in a column, with the ones under the ones. All this is connected by the multiplication sign ( x )
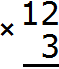
Next, each digit of a multi-digit number is multiplied by 3. We start multiplying from the digit one, that is, from the digit 2. Two multiplied by three is six. Write the digit 6 in the units division of our answer:
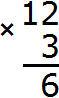
If both numbers end with zeros, then multiply those digits that are not zeros, then add all zeros from both numbers to the result.
Example 1. multiply 20 by 30.
20 x 30
We see that both numbers contain zero. First we multiply the digits that are not zeros. These are the digits two and three. Two multiplied by three is six:
20 x 30 = 6
Now add all zeros from both numbers to the result, that is, to the number 6. Number 20 has one zero, number 30 also has one zero. Total two zeros. We add two zeros to number 6
20 x 30 = 600
Multiplying decimals by 10, 100 or 1000 is done in the same way as multiplying decimals by regular numbers.
You must do the multiplication without paying attention to the dot in the decimal, then separate the whole part from the fractional part in the answer by counting off as many digits to the right as there were digits after the dot in the decimal.
For example, multiply 2.88 by 10
Multiply the decimal 2.88 by 10, ignoring the dot in the decimal:
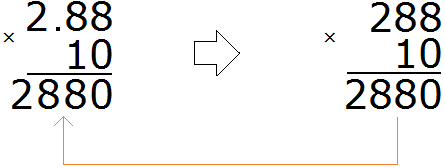
We got 2880. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in the fraction 2.88. We see that there are two digits after the dot in the fraction 2.88.
Go back to the number 2880 and start moving from right to left. We need to count the two digits to the right and put a dot:

The answer is 28.80. We discard the last zero and get 28.8. So the value of the expression 2.88×10 is 28.8
2.88 × 10 = 28.8
Decimals, like regular numbers, have their own digits. These are the digits of tenths, digits of hundredths, and digits of thousandths. In this case, the digits begin after the point.
The first digit after the point is the decimal place, the second digit after the point is the hundredth place, and the third digit after the point is the thousandth place.
Digits in decimals store some useful information. In particular, they tell you how many tenths, hundredths, and thousandths there are in a decimals.
For example, consider the decimal 0.345
The position where the triple is located is called the digit of tenths
The position where there is a four is called the hundredths digit
The position where there is a five is called the digit of thousandths
Definition. A prime is a number that is divisible by itself and 1 without a remainder. In other words, it has only two divisors.
For example, number 5 is divisible by itself and one without a remainder:
5 : 1 = 5
5 : 5 = 1
So the number 5 is a prime number.
Definition. A composite number is a number that has two or more divisors.
For example, number 4 is a composite number because it has two or more divisors: 4, 2, and 1.
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
So the number 4 is a composite number.
Video lesson
Any composite number can be factorized into prime factors. We did something similar in the lesson on substitution in expressions. In this lesson we learned that any number in an expression can be replaced by the same number but written in a different form.
For example, the number 6 can be written as the sum of 4 + 2 or as the quotient 12 : 2 or as the product 2 × 3. The last entry 2 × 3 can be called a decomposition of the number 6 into prime factors.
The essence of the decomposition of a number into prime factors is to represent this number as a product of several prime factors.
Let's decompose the number 4 into prime factors. To do this, we gather this number from other numbers, and write them with the multiplication sign (×). The number 4 is composed of the numbers 2 and 2. These two numbers are simple multipliers that make up the number 4
4 = 2 × 2
Early on in our study of fractions, we learned that a proper fraction is one in which the numerator is smaller than the denominator.
In school books we can find another definition of a proper fraction. It looks like this:
"A proper fraction is always less than 1."
How do we understand this definition? A fraction by itself indicates that some object is divided into several parts. And it is always one single object. This is what is meant by a unit.
For example, let's say we have one pizza:

In this case, it is the unit.
If we cut off half of this pizza, that is, ![]() (one-second of the pizza), then our slice will be smaller than the whole pizza:
(one-second of the pizza), then our slice will be smaller than the whole pizza:
Page 7 of 9