Place value with decimals

Decimals, like regular numbers, have their own digits. These are the digits of tenths, digits of hundredths, and digits of thousandths. In this case, the digits begin after the point.

The first digit after the point is the decimal place, the second digit after the point is the hundredth place, and the third digit after the point is the thousandth place.

Digits in decimals store some useful information. In particular, they tell you how many tenths, hundredths, and thousandths there are in a decimals.

For example, consider the decimal 0.345

The position where the triple is located is called the digit of tenths

The position where there is a four is called the hundredths digit

The position where there is a five is called the digit of thousandths

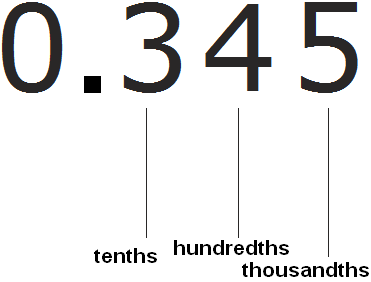
Let's look at this picture. We see that there is a three in the decimal place. This tells us that the decimal 0.345 contains three tenths of .

Let's see further. In the hundredths digit there is a four. This indicates that the decimal 0.345 contains four hundredths of .

Let's see further. In the thousandth digit is a five. This indicates that the decimal 0.345 contains five thousandths of .

If we add the fractions, and , we get the original decimal 0.345

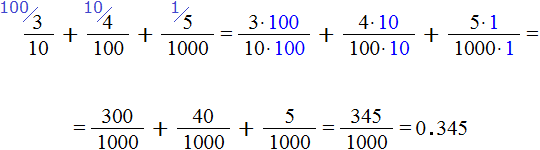
At first we got the answer , but we converted it to a decimal and got 0.345.

When adding decimals, the same rules are followed as when adding regular numbers. The addition of decimals is done by digits: tenths are added to tenths, hundredths to hundredths, and thousandths to thousandths.

Therefore, when adding decimals, the rule "point under the point" must be followed. The point under the point provides the very order in which the tenths add up to the tenths, the hundredths to the hundredths, and the thousandths to the thousandths.

Example 1. Find the value of the expression 1.5 + 3.4

Write the expression in columns, following the rule "point under the point":

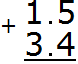
First add the fractional parts 5 + 4 = 9. Write the nine in the fractional part of our answer:

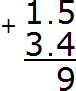
Now add the integers 1 + 3 = 4. Write the four in the whole part of our answer:

Now separate the whole part from the fractional part with a dot. To do this, again follow the rule "point under the point":

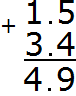
The answer is 4.9. So the value of the expression 1.5 + 3.4 is 4.9

1.5 + 3.4 = 4.9

Example 2. Find the value of the expression: 3.51 + 1.22

Write down the expression in columns, following the rule "point under the point".

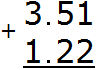
First, we add the fractional part, namely the hundredths part 1+2=3. Write the three in the hundredth part of our answer:

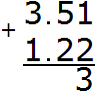
Now add the tenths of 5+2=7. Write the seven in the tenth of our answer:

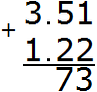
Now add the whole parts 3+1=4. Write the four in the whole part of our answer:

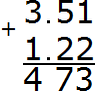
Separate the whole part from the fractional part with a dot, observing the rule "point under the point":

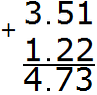
The answer is 4.73. So the value of the expression 3.51 + 1.22 is 4.73

3.51 + 1.22 = 4.73

As with regular numbers, adding decimals may cause a digit overflow. In this case, one digit is written in the answer, and the rest is transferred to the next digit.

Example 3. Find the value of the expression 2.65 + 3.27

Write the expression in columns:

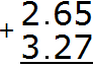
We add the hundredths of 5+7=12. The number 12 will not fit in the hundredth part of our answer. Therefore, write the number 2 in the hundredth part, and carry the one to the next digit:

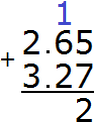
Now add the tenths of 6+2=8 plus the one we got from the previous operation, we get 9. Write the number 9 in the tenth part of our answer:

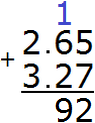
Now add the integers 2+3=5. Write the number 5 in the whole part of our answer:

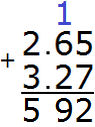
Separate the whole part from the fractional part with a dot:

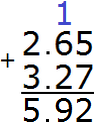
The answer is 5.92. So the value of the expression 2.65 + 3.27 is 5.92

2.65 + 3.27 = 5.92

Example 4. Find the value of the expression 9.5 + 2.8

Write the expression in the column

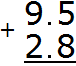
We add the fractional parts 5 + 8 = 13. The number 13 will not fit into the fractional part of our answer, so we write the number 3 first, and carry the one to the next digit, or rather, carry it to the whole part:

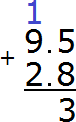
Now add the integers 9+2=11 plus the one we got from the previous operation, we get 12. Write the number 12 in the whole part of our answer:

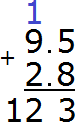
Separate the whole part from the fractional part with a dot:

The answer is 12.3. So the value of the expression 9.5 + 2.8 is 12.3

9.5 + 2.8 = 12.3

When adding decimals, the number of digits after the point in both fractions must be the same. If there are not enough digits, these places in the fractional part are filled with zeros.

Example 5. Find the value of the expression: 12.725 + 1.7

Before writing the expression in the column, make the number of digits after the decimal point in both fractions the same. The decimal 12.725 has three digits after the decimal point, while the fraction 1.7 has only one. So in the fraction 1.7, we need to add two zeros at the end. Then we have a fraction 1.700. Now we can write down the expression in columns and start calculating:

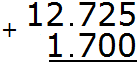
Add up the thousandths of 5+0=5. Write the number 5 in the thousandth part of our answer:

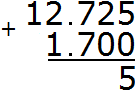
Add the hundredths of 2+0=2. Write the number 2 in the hundredth part of our answer:

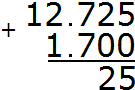
Add up the tenths 7+7=14. The number 14 will not fit in the tenth part of our answer. So we write the number 4 first, and carry the one to the next digit:

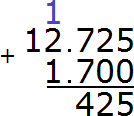
Now add the integers 12+1=13 plus the one we got from the previous operation, we get 14. Write the number 14 in the whole part of our answer:

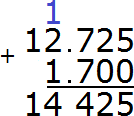
Separate the whole part from the fractional part with a dot:

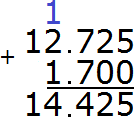
The answer is 14,425. So the value of the expression 12.725+1.700 is 14.425

12.725+ 1.700 = 14.425

Video lesson

Add comment