Multiplying decimals by 0.1, 0.01 and 0.001 is done in the same way as multiplying a decimal by a decimal.
It is necessary to multiply fractions like regular numbers and put a dot in the answer, counting as many digits to the right as there are digits after the dot in both fractions.
For example, multiply 3.25 by 0.1
Multiply these fractions like regular numbers, ignoring the dots:
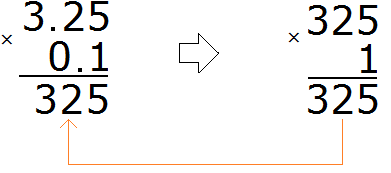
We got 325. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the point in fractions 3.25 and 0.1. There are two digits after the dot in fraction 3.25 and one digit in fraction 0.1. The total is three digits.
Go back to 325 and start moving from right to left. We need to count three digits to the right and put a dot. After counting the three digits, we find that the digits have run out. In this case we need to add one zero and put a dot:
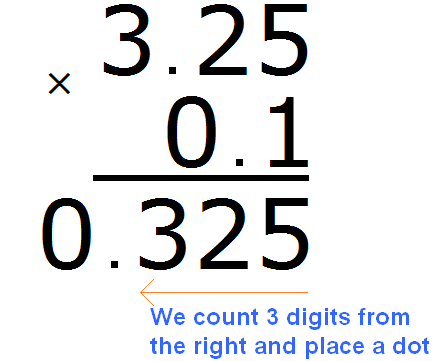
The answer is 0.325. So the value of the expression 3.25 × 0.1 is 0.325
3.25 × 0.1 = 0,325
There is a second way to multiply decimals by 0.1, 0.01 and 0.001. This method is much easier and more convenient. It consists in the fact that the point in the decimal is moved to the left by as many digits as zeros in the multiplier.
For example, solve the previous example 3.25 × 0.1 this way. Without giving any calculations, we immediately look at the multiplier 0.1. We are interested in how many zeros it contains. We see that it contains one zero. Now, in the fraction 3.25, move the decimal point to the left by one digit. Having moved the dot one digit to the left, we see that there are no more digits before the three. In this case, add one zero and put a dot. The result is 0.325
3.25 × 0.1 = 0,325
Let's try to multiply 3.25 by 0.01. Immediately we look at the multiplier 0.01. We are interested in how many zeros it contains. We see that it has two zeros. Now in the fraction 3.25 move the point to the left by two digits, we get 0.0325
3.25 × 0,01 = 0.0325
Let's try multiplying 3.25 by 0.001. Immediately we look at the multiplier 0.001. We are interested in how many zeros it contains. We see that it has three zeros. Now in the fraction 3.25 we move the point to the left by three digits, we get 0.00325
3.25 × 0.001 = 0.00325
Do not confuse multiplying decimals by 0.1, 0.001, and 0.001 with multiplying by 10, 100, and 1000. A typical mistake most people make.
When multiplying by 10, 100, 1000, the point is moved to the right by as many digits as there are zeros in the multiplier.
And when multiplying by 0.1, 0.01 and 0.001, the point is moved to the left as many digits as there are zeros in the multiplier.
If this is difficult to remember at first, you can use the first method, in which multiplication is done as with regular numbers. In the answer, you will need to separate the whole part from the fractional part by counting off as many digits to the right as there are digits after the point in both fractions.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.