Prime Factor Decomposition

Any composite number can be factorized into prime factors. We did something similar in the lesson on substitution in expressions. In this lesson we learned that any number in an expression can be replaced by the same number but written in a different form.

For example, the number 6 can be written as the sum of 4 + 2 or as the quotient 12 : 2 or as the product 2 × 3. The last entry 2 × 3 can be called a decomposition of the number 6 into prime factors.

The essence of the decomposition of a number into prime factors is to represent this number as a product of several prime factors.

Let's decompose the number 4 into prime factors. To do this, we gather this number from other numbers, and write them with the multiplication sign (×). The number 4 is composed of the numbers 2 and 2. These two numbers are simple multipliers that make up the number 4

4 = 2 × 2

Decompose the number 6 into factors. The number 6 can be assembled from the numbers 2 and 3. These two numbers are the simple multipliers that make up number 6

6 = 2 × 3

Decompose the number 8 into factors. This number can be decomposed into factors 2 and 4, and the factor 4 can be decomposed into two factors: 2 and 2. So we write its decomposition instead of the four:

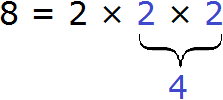
Large numbers are decomposed in the same way. First they are decomposed into large multipliers, then these large multipliers are decomposed into small multipliers. And so on until each multiplier becomes a prime number.

For example, let's decompose the number 180 into prime factors. The number 180 is two multipliers 18 and 10

180 = 18 × 10

Now decompose the multipliers 18 and 10 into other multipliers:

18 = 3 × 6

10 = 5 × 2

Now decompose the highlighted blue six. This is the last large multiplier that can be decomposed into prime multipliers:

6 = 2 × 3

Now put all the simple multipliers together:

Only a composite number can be decomposed into multipliers. A prime number cannot be decomposed into multipliers. That is why when the decomposition reaches prime numbers, we do not decompose the prime numbers further.

There is a second method of decomposition into prime factors. It is simpler and better suited for large numbers. The essence of this method is that first draw a vertical line. Then to the left of this line are written divisors, and to the right - divisors, which are later collected into multipliers.

When decomposing a number by this method, the signs of divisibility are used, such as: the signs of divisibility by 2, by 3, by 5 and others.

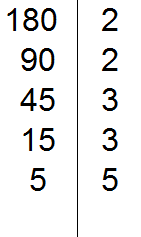
For example, decompose the previous number 180 this way.

Draw a vertical line and on the left side write the first divisor of 180

Now we apply the signs of divisibility. First, we check if 180 is divisible by 2. If it is divisible, you should write this two to the right of the vertical line.

180 is divisible by 2 because 180 ends in zero. Write the two to the right of the vertical line:

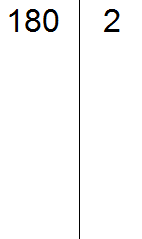
Now divide 180 by 2 and get the second divisor 90. Write this divisor to the left of the vertical line:

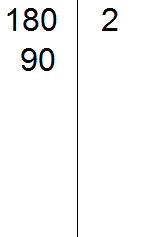
Now divide by 90. Again we apply the signs of divisibility. We check if 90 is divisible by 2.

90 is divisible by 2 because 90 ends in zero. Write the two to the right of the vertical line:

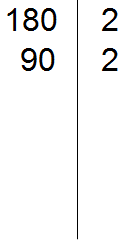
Now divide 90 by 2 to get the third divisor 45. Write this divisor to the left of the vertical line:

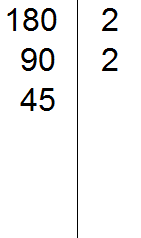
Now divide by 45. Again we apply the signs of divisibility. Check if 45 is divisible by 2.

45 is not divisible by 2. Then we check if 45 is divisible by 3.

45 is divisible by 3, because the sum of digits 4 and 5 is divisible by 3. Write the 3 to the right of the vertical line:

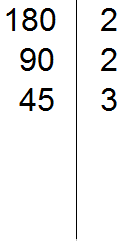
We divide 45 by 3 to get the fourth divisor 15. Write this divisor to the left of the vertical line:

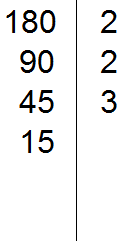
Now divide 15. We check if 15 is divisible by 2.

15 is not divisible by 2. Then we check if 15 is divisible by 3.

15 is divisible by 3, because the sum of digits 1 and 5 is divisible by 3. Write the 3 to the right of the vertical line:

We divide 15 by 3, so we get the fifth divisor 5. Write the five to the left of the vertical line:

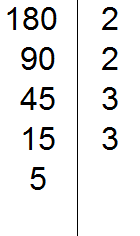
Now divide 5. We check if 5 is divisible by 2.

5 is not divisible by 2. Then we check if 5 is divisible by 3.

5 is not divisible by 3. Then we check if 5 is divisible by 5.

5 is divisible by 5. Write this 5 to the right of the vertical line:

We divide 5 by 5 and get the sixth divisor 1. Write this one to the left of the vertical line:

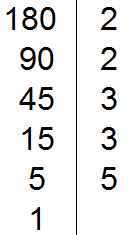
This completes the division, since we have reached one. The divisors that are written to the right of the vertical line must be prime numbers. So when the divisor 5 did not divide by 2 and then did not divide by 3, we tried to divide it by 5 without trying to divide by 4 because 4 is not a prime but a composite number.

Now we write down in one row all the divisors that are written to the right of the vertical line. They will be the decomposition of number 180 into prime factors. It is desirable to write them down, starting with the smallest. This allows you to order them in ascending order:

Don't be upset if you have trouble decomposing numbers into prime factors. This topic requires a little practice. For practice you can decompose the following numbers into prime factors: 256, 378, 512.

Video lesson

Add comment