Fractions can be simplified. To reduce means to make a fraction shorter and easier to understand. For example, a fraction![]() looks much simpler and prettier than
looks much simpler and prettier than ![]() .
.
If you get a big fraction when you solve the examples, you should try to reduce it.
Fraction reduction relies on the basic property of fractions. Therefore, before learning how to reduce fractions, be sure to learn the basic property of fractions.
Dividing the numerator and denominator by their greatest common divisor is called fraction reduction or simplification.
Example 1. Simplify a fraction ![]()
So, we need to divide the numerator and denominator of the fraction![]() on the greatest common divisor of 2 and 4.
on the greatest common divisor of 2 and 4.
In this case, the fraction is simple and its GCD is easy to find. The GCD of 2 and 4 is 2. Therefore, the numerator and denominator of the fraction ![]() must be divided by 2
must be divided by 2
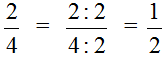
As a result, the fraction ![]() has become a simpler fraction
has become a simpler fraction ![]() . The value of the original fraction did not change, because reduction involves dividing the numerator and denominator by the same number. And this action, as stated earlier, does not change the value of the fraction.
. The value of the original fraction did not change, because reduction involves dividing the numerator and denominator by the same number. And this action, as stated earlier, does not change the value of the fraction.
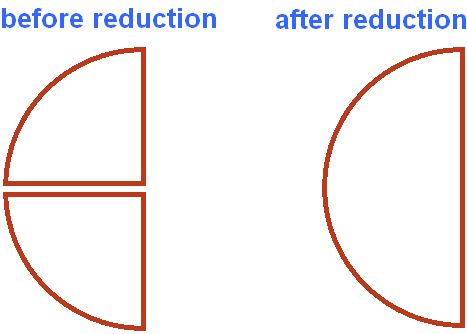
The figure shows fractions ![]() and
and ![]() as slices of pizza. Before the reduction and after the reduction they have the same size. The only difference is that they are cut differently.
as slices of pizza. Before the reduction and after the reduction they have the same size. The only difference is that they are cut differently.
Example 2. Let's reduce the fraction ![]()
To reduce the fraction![]() , you need to divide the numerator and denominator of this fraction by the greatest common divisor of the numbers 20 and 40.
, you need to divide the numerator and denominator of this fraction by the greatest common divisor of the numbers 20 and 40.
The GCD of 20 and 40 is 20. Therefore, divide the numerator and denominator of fraction![]() by 20
by 20
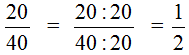
Example 3. Let's reduce the fraction ![]()
To reduce the fraction![]() , you need to divide the numerator and denominator of this fraction by the greatest common divisor of 32 and 36.
, you need to divide the numerator and denominator of this fraction by the greatest common divisor of 32 and 36.
The GCD of 32 and 36 is number 4. Therefore, divide the numerator and denominator of the fraction ![]() by 4
by 4
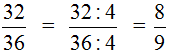
If there are prime numbers in the numerator and denominator, the fraction cannot be reduced - it is not reduced. Such fractions are called irreducible. For example, the following fractions are irreducible:
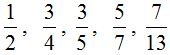
Recall that prime numbers are numbers that are divided only by one and themselves.
The second way to reduce fractions
The second method is a short version of the first method. Its essence is that a detailed explanation of what the numerator and denominator were divided into is omitted.
For example, let's return to fractions ![]() . We reduced this fraction by 4, that is, we divided the numerator and denominator of this fraction by the number 4
. We reduced this fraction by 4, that is, we divided the numerator and denominator of this fraction by the number 4
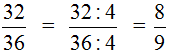
Now imagine that this expression does not contain the construction ![]() , and immediately recorded the answer
, and immediately recorded the answer ![]() . You get the following expression:
. You get the following expression:
![]()
The point is that the number by which the numerator and denominator are divided is kept in mind. In our case, the numerator and denominator divide by 4 - this is the number we will store in our mind.
First divide the numerator by the number 4. The answer is written next to the numerator, crossing it out:
![]()
Then divide the denominator by 4 in the same way. Write the answer next to the denominator, crossing it out beforehand:
![]()
Then we assemble a new fraction. In the numerator we send a new number 8 instead of 32, and in the denominator we send a new number 9 instead of 36
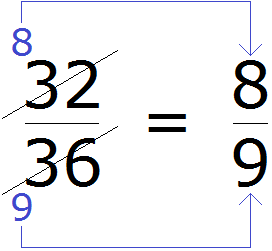
A kind of replacement of one fraction with another takes place. The value of the new fraction equals the value of the previous fraction, because the basic property of fractions works, which says that if the numerator and denominator of a fraction are multiplied or divided by the same number, we get a fraction equal to it.
Also, fractions can be reduced by first decomposing the numerator and denominator into prime factors.
For example, let's reduce a fraction ![]() , by first decomposing the numerator and denominator into prime factors:
, by first decomposing the numerator and denominator into prime factors:
![]()
So, we decomposed the numerator and denominator of the fraction ![]() into multipliers. Now we apply the second method of reduction. In the numerator and in the denominator select a factor and divide the selected factors by the GCD of these factors.
into multipliers. Now we apply the second method of reduction. In the numerator and in the denominator select a factor and divide the selected factors by the GCD of these factors.
Let's reduce each triplet in the numerator and denominator. To do this, divide these triples by 3 (by their greatest common divisor). We obtain the following expression:

You can also cut down on the three in the numerator and denominator:

There is nothing else to reduce. The last three in the denominator cannot be simply reduced, because there is no factor in the numerator that can be reduced together with this three.
Write a new fraction with new multipliers in the numerator and denominator.
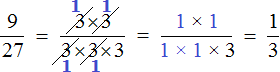
We got the answer ![]() . So, when reducing a fraction
. So, when reducing a fraction ![]() you get a new fraction
you get a new fraction ![]() .
.
It is not recommended to use the second method of reduction of fractions and the method of expansion into simple multipliers of the numerator and denominator, if a person is just beginning to learn mathematics. Practice shows that this proves to be difficult at first stages.
So if you have trouble using the second method, use the good old method of reduction: divide the numerator and denominator of the fraction by their greatest common divisor. The expression in this case is simple, clear, and beautiful. For example, the previous example can be solved the old way and will look like this:
![]()
Compare this expression with the expression we got when we used the second method:
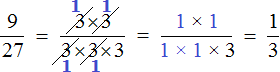
The first expression is much clearer, neater, and shorter. Isn't it?



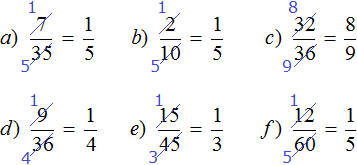
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.