To multiply a multi-digit number by a single-digit number, multiply each digit of the multi-digit number by that single-digit number. For example, find the value of the expression 12 x 3. Write this expression in a column, with the ones under the ones. All this is connected by the multiplication sign ( x )
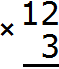
Next, each digit of a multi-digit number is multiplied by 3. We start multiplying from the digit one, that is, from the digit 2. Two multiplied by three is six. Write the digit 6 in the units division of our answer:
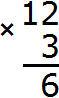
Now multiply 1 by 3 to get 3. Write the number 3 in the tens place of our answer:
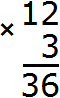
The answer is 36.
In this example, the multiplier was 12 and the multiplier was 3. The number 12 is two ones and one tens. Our problem was to increase these two ones and one tens by a factor of 3. Then, solving this example, we could reason as follows:
Increase two units by a factor of three: 2 x 3 = 6. We have six units. Write the number 6 in the units division of the new number
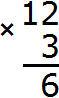
Let's increase one tens by three times: 1 x 3 = 3. We have three tens. Write the number 3 in the tens division of the new number:
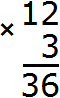
Sometimes multiplying one digit of a multi-digit number by a single-digit number results in a multi-digit number. In this case, first write down one digit from the units digit, and transfer the remaining digits to the next digit to which they will be added after the calculation.
For example, find the value of the expression 23 x 6
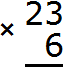
Multiply each digit of 23 by 6. We start with a 3: 3 x 6 = 18. Eighteen does not fit in the unit digit of our answer, so 8 is written first, and 1 is carried over to the next digit. This unit will be added to the result of multiplying 2 by 6.

Now multiply 2 by 6 to get 12, plus the one that came from the previous multiplication. In the figure this unit is highlighted in blue. Calculate (2 x 6) + 1 = 13
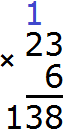
The answer is 138. In this example, the multiplier was 23 and the multiplier was 6. The number 23 is three ones and two tens.. Our problem was to increase these three units and two tens by a factor of 6. Then, solving this example, we could reason as follows:
Let's increase three units six times: 3 x 6 = 18. We got eighteen units. There is a digit overflow in the ones place value. Eighteen is eight ones and one tenth. Write 8 ones in the units category of the new number, and 1 tens in the tens category. We will add this tens when we increase two tens six times:

Let's increase two tens 6 times: 2 x 6 = 12. We have twelve tens. Add one tens left over from number 18.
Twelve tens plus one tenth is 13. Write 13 in the place of tens of the new number, forming the final answer:
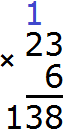
Example 3. Find the value of the expression 326 x 5
Write the expression in columns:
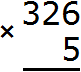
Multiply each digit of 326 by 5. We start with a six: 6 x 5 = 30. The number 30 does not fit in the units digit of our answer, so we write 0 first, and carry the three to the next digit:
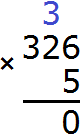
Now multiply 2 by 5, and we get 10 plus the three that came from the previous operation: (2 x 5) + 3 = 13. We obtain the number 13, which does not fit in the digit of tens of our answer. Therefore, we write down 3 first, and carry the one to the next digit:
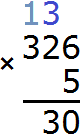
Now multiply the last three by 5, plus add the one that came from the previous operation: (3 x 5) + 1 = 16. We obtained 16. Write down this number in its entirety, forming the final answer:
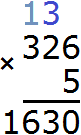
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.