Early on in our study of fractions, we learned that a proper fraction is one in which the numerator is smaller than the denominator.
In school books we can find another definition of a proper fraction. It looks like this:
"A proper fraction is always less than 1."
How do we understand this definition? A fraction by itself indicates that some object is divided into several parts. And it is always one single object. This is what is meant by a unit.
For example, let's say we have one pizza:

In this case, it is the unit.
If we cut off half of this pizza, that is, ![]() (one-second of the pizza), then our slice will be smaller than the whole pizza:
(one-second of the pizza), then our slice will be smaller than the whole pizza:

This is the essence of the phrase "a proper fraction is always less than one".
Our pizza half is a fraction of ![]() and it is less than one whole pizza, which is less than one:
and it is less than one whole pizza, which is less than one:
![]()
This expression can be proved. If we calculate the fraction ![]() , we get the decimal 0.5. And this is a rational number less than one:
, we get the decimal 0.5. And this is a rational number less than one:
![]()
On the number line you can see how these numbers are arranged:

You can see that the rational number 0.5 is to the left of 1. And we remember that the more to the left of the number on the number line, the smaller it is.
With improper fractions, it was the opposite. We called an improper fraction a fraction where the numerator is larger than the denominator.
But in school books you can find another definition of an improper fraction. It looks like this:
"An improper fraction is always greater than or equal to one."
For example, consider the improper fraction ![]() . Separate the whole part of the fraction, so we get
. Separate the whole part of the fraction, so we get ![]() . Let's represent this mixed number as one whole pizza and another half pizza:
. Let's represent this mixed number as one whole pizza and another half pizza:
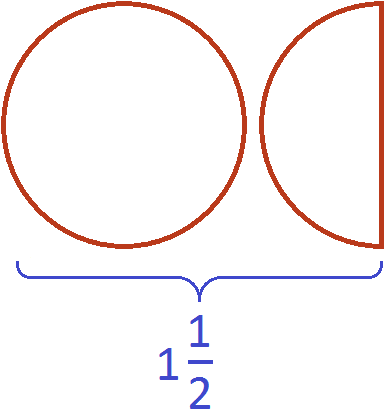
Together one whole pizza and another half pizza is more than just one whole pizza
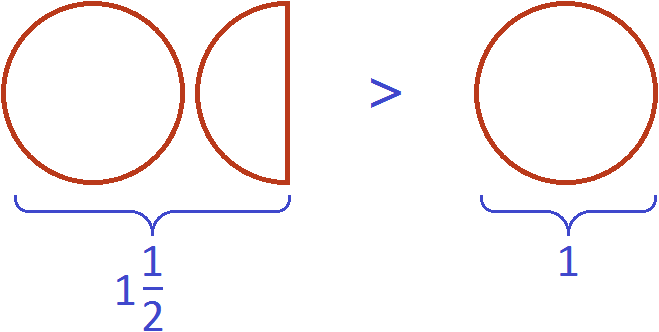
This is the essence of the phrase "an improper fraction is always greater than one".
One whole pizza and another half pizza is described by a mixed number of ![]() and that mixed number is greater than one:
and that mixed number is greater than one:
![]()
Let's convert the mixed number ![]() back to an improper fraction so as not to contradict the rule. After all, in this case we are talking about improper fractions:
back to an improper fraction so as not to contradict the rule. After all, in this case we are talking about improper fractions:
![]()
which schematically would look like this:
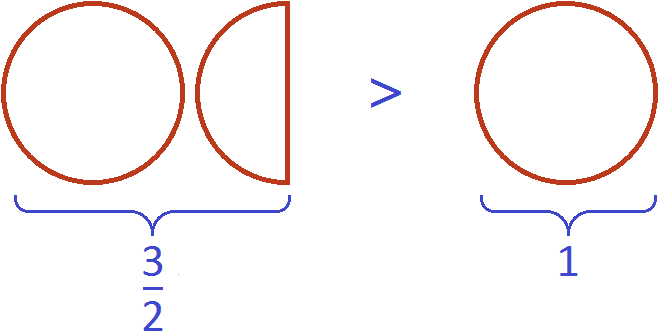
The expression ![]() can be proved. If we calculate the fraction
can be proved. If we calculate the fraction ![]() , we get the decimal 1.5. And this is a rational number greater than one:
, we get the decimal 1.5. And this is a rational number greater than one:
![]()
On the number line you can see how these numbers are arranged:

You can see that the rational number 1.5 is more to the right than 1. And we remember that the more right the number is on the number line, the larger it is.
A fraction equal to one is also called an improper fraction. We are talking about those fractions in which the numerator and denominator are equal.
Consider the fraction ![]() . Picture it as two identical slices of pizza:
. Picture it as two identical slices of pizza:
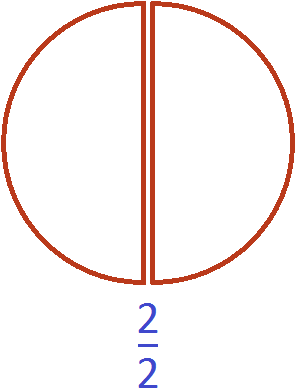
In fact, we are not talking about fractions, but one whole pizza:
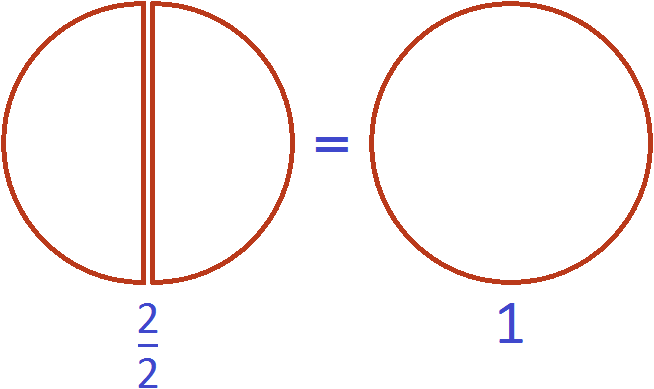
This is the essence of the phrase "an improper fraction can equal one".
![]()
Any integer other than zero (not equal to zero) can be represented as an improper fraction with a denominator of 1. For example, the numbers 3, 5, 9, 12 can be represented as improper fractions with denominator 1
![]()
Representing an object as a unit makes it easier to solve problems. Let's look at some examples.
Example 1. One chocolate bar is bought. A third of it was cut off. How many bars are left?
Two-thirds of the candy bar is left. The candy bar itself can be described by the number 1, then subtract a third from that unit:
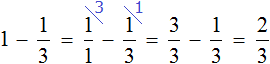

Without giving any calculations on paper, it is possible to answer the question of such a problem. If you say "cut off a third", then you should immediately note that the denominator is 3.
If you cut off one part out of three, how many parts should be left? That's right, two parts. So the answer is "two parts of three" or "two-thirds".
Example 2. One pie is bought. Two sixths of it were cut off. How many pies are left?
There are four sixths of a pie left. The pie itself can be described by the number 1, then subtract two sixths from this unit:
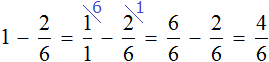
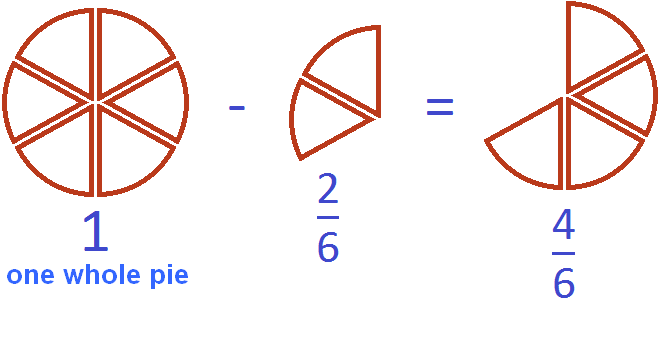
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.