There are problems in which you need to add mixed numbers. For example, to find the value of the expression ![]() . To solve this example, you need to add the whole and fractional parts separately.
. To solve this example, you need to add the whole and fractional parts separately.
First, let's write down the mixed numbers in expanded form:
![]()
Apply the combinative law of addition. Group the whole and fractional parts separately:
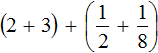
Let's calculate the integers: 2 + 3 = 5. In the main expression, replace the expression in parentheses (2 + 3) with the resulting five:
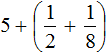
Now let's calculate the fractional parts. This is the addition of fractions with different denominators. We already know how to add such fractions:
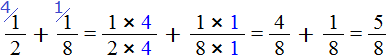
We got ![]() . Now in the main expression
. Now in the main expression 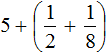 replace the fractional parts with the resulting fraction
replace the fractional parts with the resulting fraction ![]() .
.
![]()
Now let's collapse the resulting mixed number:
![]()
Thus, the value of the expression ![]() is
is ![]() . Let's try to represent this solution in the form of a picture. If you add three whole pizzas and an eighth to two whole pizzas and a half, you get five whole pizzas and five eighths of pizzas:
. Let's try to represent this solution in the form of a picture. If you add three whole pizzas and an eighth to two whole pizzas and a half, you get five whole pizzas and five eighths of pizzas:
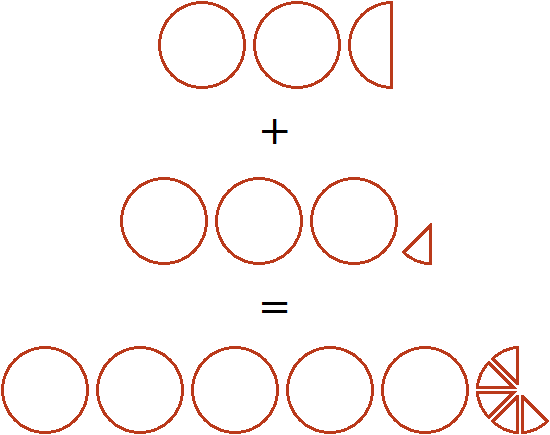
Examples like this need to be solved quickly, without stopping for details. If we were in school, we would have to write down the solution to this example as follows:
![]()
If you see such a short solution in the future, don't be frightened. You already understand where it came from.
Example 2. Find the value of the expression ![]()
Let's write the mixed numbers in expanded form:
![]()
Let's group the integers and fractions separately:
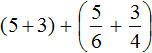
Let's calculate the integers: 5 + 3 = 8. In the main expression, replace the expression in parentheses (5 + 3) with the resulting number 8
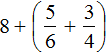
Now let's calculate the fractional parts:
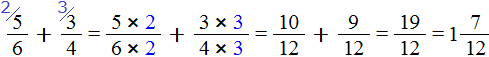
We obtained a mixed number of ![]() . Now replace the expression in parentheses in the main expression
. Now replace the expression in parentheses in the main expression 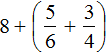 with the resulting mixed number
with the resulting mixed number ![]()
![]()
We got the expression ![]() . In this case, the number 8 must be added to the integer part of the mixed number
. In this case, the number 8 must be added to the integer part of the mixed number ![]() . To do this, the mixed number
. To do this, the mixed number ![]() can be temporarily expanded to make it clearer what to add to what:
can be temporarily expanded to make it clearer what to add to what:
![]()
Let's add the whole parts. We get 9
![]()
We wrap up the finished answer:
![]()
Thus, the value of the expression ![]() is
is ![]() .
.
The complete solution of this example is as follows:
![]()
There is a universal rule for solving such examples. It looks like this:
To add up mixed numbers, you have to:
- reduce the fractional parts of these numbers to a common denominator;
- perform addition of integers and fractions separately.
If adding fractions results in an improper fraction, isolate the integer part of the fraction and add it to the resulting whole.
The use of ready-made rules is acceptable if the essence of the topic is fully understood. A formulaic solution, looking at other similar examples, leads to errors that take extra time to find. Therefore, it is more reasonable to understand the topic first, and then use a ready-made rule.
Example 3. Find the value of the expression ![]()
Let's use a ready-made rule. Let's reduce the fractional parts to a common denominator, then add the whole and fractional parts separately:
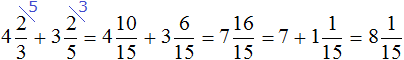
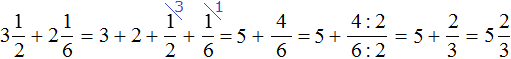
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.