Adding whole number to a fraction

You may encounter problems in which you need to add a whole number and a fraction. For example, add a number 2 and a fraction. To solve this example, you need to represent the number 2 as a fraction . Then add fractions with different denominators:

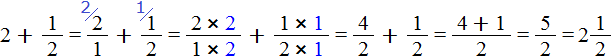
Now look carefully at this example. Let's look at the beginning and the end of it. Its beginning looks like this: , and the end is this: . The difference is that in the first case the number 2 and the fraction are joined by an addition sign, and in the second case they are written together. In fact, this is the same thing. The point is that is a convolute form of a mixed number, and is an expanded form.

When we have a mixed number of the form in front of us, we must realize that the addition sign is omitted.

What conclusion can be drawn? If you need to add a number to a proper fraction, you can omit the plus sign and write the integer number and fraction together.

So the value of the expression is

If you add half a pizza to two whole pizzas, you get two whole pizzas and half a pizza:

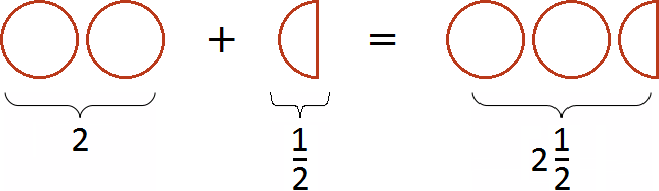
Example 2. Find the value of the expression

Let's represent the number 3 as a fraction of . Then add fractions with different denominators:

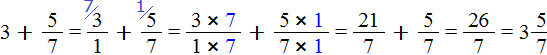
This is the first way. The second way is much easier. You can put an equal sign and write the integer part and the fractional part together. That is, omit the addition sign:

Example 3. Find the value of the expression

You can write the number 2 and the fraction together, but that answer will not be final because you can separate the integer part in the fraction .

Therefore, in this example, you must first isolate the integer part in the fraction . Five second fractions are two integers and one second:

Now, in the main expression we write the mixed number instead of the fraction

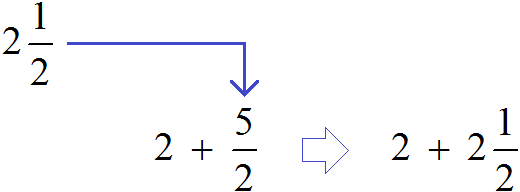
We have a new expression . In this expression, write the mixed number in expanded form:

Apply the combinative law of addition. If we add two twos, we get 4:

Now let's roll up the resulting mixed number:

This is the final answer. The detailed solution of this example can be written as follows:

Exercises

Task 1. Find the value of the expression:

Solution:

Show Solution

Task 2. Find the value of the expression:

Solution:

Show Solution

Task 3. Find the value of the expression:

Solution:

Show Solution

Video lesson

Add comment