Calculate the fraction
. Five divided by two will be two and one in the remainder:
5 : 2 = 2 (1 in the remainder)
Verification: (2 × 2) + 1 = 4 + 1 = 5
But now we are dealing with fractions, so we have to answer in fractional form. To get a good understanding of how to do this, let's look at an example from life.
Imagine you have five apples and decide to share them with your friend. And share them fair and square, so that everyone gets the same. How do you divide these five apples?
Obviously, each of you will get two apples, and you will cut the remaining one apple in half with a knife and divide it among yourselves as well:
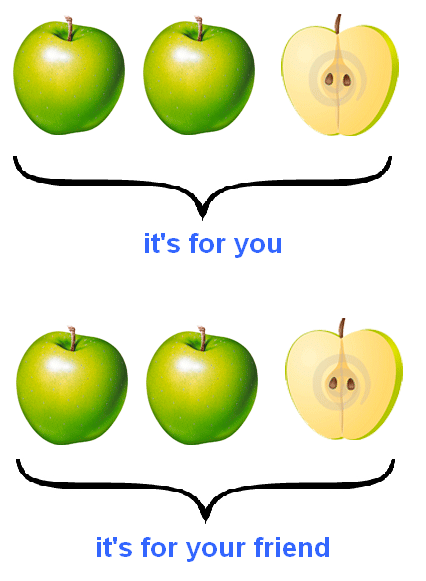
Look carefully at this picture. It shows how the five apples are divided between you and your friend. Obviously, everyone got two whole apples and a half of an apple.
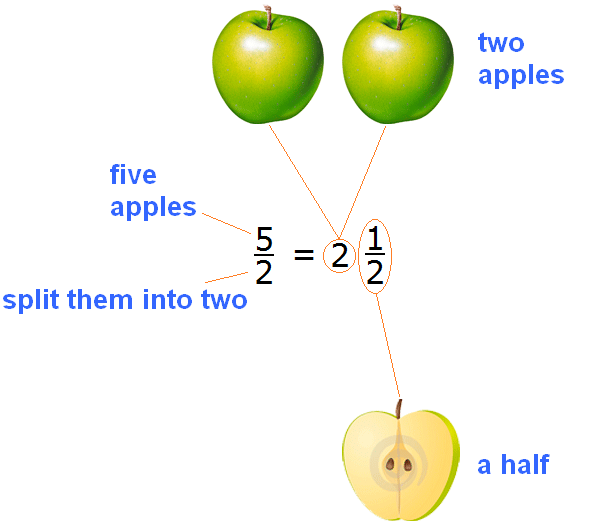
Now go back to the fraction and answer her question. Whats the result of division? We look at our picture and answer: if five apples are divided by two, each of them will get two whole apples and a half of an apple. Let's write it down this way:
Schematically it looks like this:
The procedure we have just performed is called the extraction of the integer part of the fraction.
In our example, we extracted the integer part of the fraction 
and got a new fraction 
. Definition. Such a fraction is called a mixed fraction. A mixed fraction is a fraction that has an integer part and a fractional part.
In our example, the integer part is 2 and the fractional part is
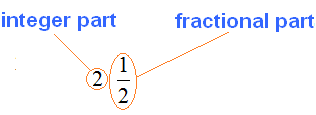
Be sure to memorize these concepts! Better yet, write them down in your workbook.
The integer part can only be extracted from improper fractions. Recall that an improper fraction is a fraction with a numerator greater than the denominator. For example, the following fractions are improper and have the integer part highlighted:
To isolate the integer part, it is enough to know how to divide numbers by an long division method. For example, select the integer part of a fraction . Write this expression in the corner and solve it:
After solving the example is completed, the new fraction is assembled like a child's constructor. It is important to understand where to put the fraction. The quotient goes to the integer part, the remainder goes to the numerator of the fractional part, and the divisor goes to the denominator of the fractional part.
In principle, if you know the multiplication table well, and can quickly perform elementary calculations in your head, you can do without writing in the corner. In schools, by the way, this is exactly what they require - that students should not waste time on simple operations, but immediately write down the answers.
But if you're just starting to learn math, we advise you to write down every little detail.
Consider another example of integer part extraction. Suppose we need to select the integer part of a fraction 
Write this expression in the corner and solve it. Then we assemble the mixed fraction:
Got it: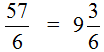 
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.