Definition. The associative law of multiplication says that there is no matter how you group numbers you are multiplying together.
Consider the following expression:
2 × 3 × 4
This expression can be calculated in any order. First you can multiply the numbers 2 and 3, and multiply the result by 4:
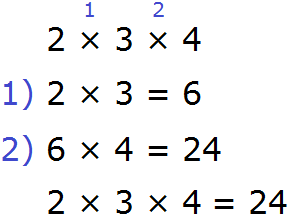
Or you can first multiply the numbers 3 and 4, and multiply the result with the number 2

Thus, between the expressions (2 × 3) × 4 and 2 × (3 × 4) we can put an equal sign, because they are equal to the same value:
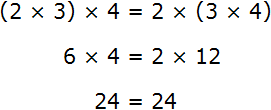
Let's write down the combinative law of multiplication using variables:
a × b × с = (a × b) × с = a × (b × с)
Example 2. Find the value of the expression 1 × 2 × 3 × 4
This expression can be calculated in any order. Let us calculate it from left to right in the order of actions:
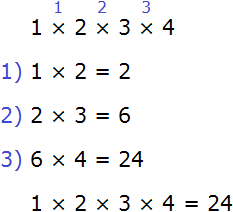
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.