Here are short articles answering one specific question.
When rounding decimals, you should be especially careful, because a decimal consists of a whole part and a fractional part. And each of these two parts has its ownplace values:
Whole place value:
- ones;
- tens;
- hundreds;
- thousands.
Fractional Part place value:
- tenths;
- hundredths;
- thousandths
Consider the decimal 123.456 - one hundred and twenty-three whole four hundred and fifty-six thousandths. Here the whole part is 123 and the fractional part is 456. Each of these parts has its own digits.
Fractions can be simplified. To reduce means to make a fraction shorter and easier to understand. For example, a fraction![]() looks much simpler and prettier than
looks much simpler and prettier than ![]() .
.
If you get a big fraction when you solve the examples, you should try to reduce it.
Fraction reduction relies on the basic property of fractions. Therefore, before learning how to reduce fractions, be sure to learn the basic property of fractions.
Dividing the numerator and denominator by their greatest common divisor is called fraction reduction or simplification.
Example 1. Simplify a fraction ![]()
First, let's introduce two new concepts: single-digit and multi-digit numbers.
Definition. A single-digit number is a number that consists of one digit. For example, the following numbers are single digits:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
The word "single digits" speaks for itself. One-digit means it consists of a single digit (a digit is sometimes called a sign).
You may encounter problems in which you want to subtract a fraction from a whole number. For example, subtract fraction ![]() from number 1. To solve such an example, imagine the whole 1 as a fraction
from number 1. To solve such an example, imagine the whole 1 as a fraction ![]() , and subtract fractions with different denominators:
, and subtract fractions with different denominators:
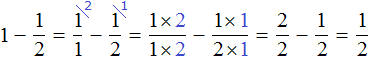
If there is one whole pizza and we subtract half a pizza from it, we have half a pizza:

Now we are ready to subtract a mixed number from a whole number. Let's find the value of the expression ![]() .
.
To solve this example, the number 5 must be presented as a fraction, and the mixed number ![]() must be converted into an improper fraction. After converting the mixed number
must be converted into an improper fraction. After converting the mixed number ![]() into an improper fraction, we obtain a fraction
into an improper fraction, we obtain a fraction ![]() . Now subtract fractions with different denominators:
. Now subtract fractions with different denominators:

If you subtract one whole pizza and one half pizza from five whole pizzas, you are left with three whole pizzas and one half pizza:

When subtracting decimals, you must follow the same rules as for addition: "point under the point" and "equal number of digits after the point".
Example 1. Find the value of the expression 2.5 - 2.2
Write the expression in columns, following the rule "point under the point":
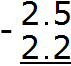
Calculate the fractional part 5-2=3. Write the number 3 in the tenth part of our answer:

Calculate the whole part 2-2=0. Write zero in the whole part of our answer:
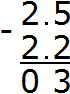
Separate the whole part from the fractional part with a dot:
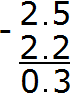
The answer is 0.3. So the value of the expression 2.5 - 2.2 is 0.3
2.5 − 2.2 = 0.3
First, we will learn how to subtract fractions with common denominators.
To subtract another fraction from one fraction, subtract the numerator of the first fraction from the numerator of the second fraction and leave the denominator unchanged.
For example, let's find the value of the expression 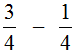 . To solve this example, subtract the numerator of the first fraction from the numerator of the second fraction and leave the denominator unchanged. Let's do that:
. To solve this example, subtract the numerator of the first fraction from the numerator of the second fraction and leave the denominator unchanged. Let's do that:
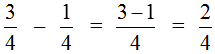
This example can be easily understood if you think of a pizza that is divided into four parts. If you cut off ![]() of the pizza from
of the pizza from ![]() of the pizza, you get
of the pizza, you get ![]() of the pizza:
of the pizza:
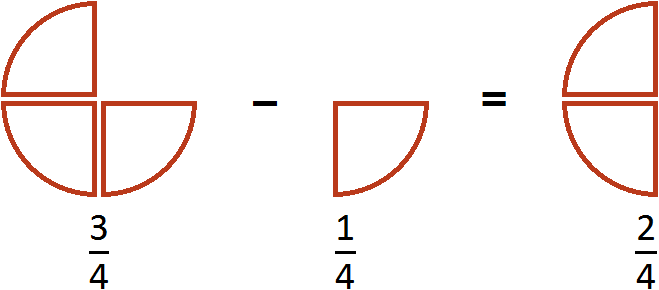
Now let's learn how to subtract fractions with different denominators. When fractions are subtracted, their denominators should be the same. But they are not always the same.
For example, you can subtract ![]() from fraction
from fraction ![]() because these fractions have the same denominators. But you cannot subtract
because these fractions have the same denominators. But you cannot subtract ![]() from fraction
from fraction ![]() because these fractions have different denominators. In such cases, the fractions must be reduced to the same (common) denominator.
because these fractions have different denominators. In such cases, the fractions must be reduced to the same (common) denominator.
The common denominator is found using the same principle we used when adding fractions with different denominators. First, we find the LCM of the denominators of both fractions. Then we divide the LCM by the denominator of the first fraction and obtain the first additional multiplier, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction to obtain the second additional multiplier, which is written over the second fraction.
There are problems where you need to subtract one mixed number from another mixed number. For example, find the value of the expression: ![]()
To solve this example, convert the mixed numbers ![]() and
and ![]() to improper fractions, then subtract fractions with different denominators:
to improper fractions, then subtract fractions with different denominators:
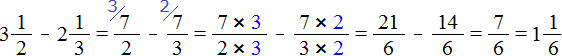
If you subtract two whole pizzas and a third of a pizza from three whole pizzas, you are left with one whole pizza and one sixth of a pizza:
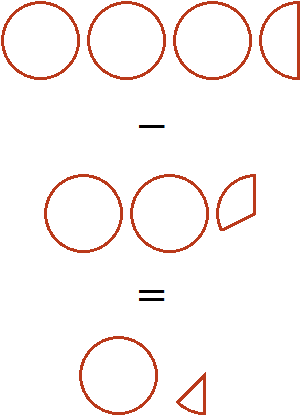
If an expression is complicated and you think it will confuse you as you solve a problem, you can put part of it into a variable, and then work with that variable.
Mathematicians often do this. They break a complex problem into easier subproblems and solve them. Then they assemble the solved subtasks into a single whole. This is a creative process, and it takes years of hard practice to learn.
The use of variables is justified when working with complex fractions. For example:
Find the value of the expression 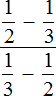
So there is a fractional expression in the numerator and a fractional expression in the denominator. In other words, we are again faced with the complex fraction that we dislike so much.
The expression in the numerator ![]() can be written into a variable with any name, for example:
can be written into a variable with any name, for example:
We know that the divisor is a number by which another number is to be divided.
For example, in the expression 8 : 2 = 4, the divisor is number 2. This number shows how many parts we need to divide number 8. After dividing it, the answer is 4. As you can see from the example, the number 8 is divisible by the number 2 without a remainder. The number 2 is said to be the divisor of number 8.
Example 1. The number 2 is a divisor of 8 because 8 is divisible by 2 without a remainder:
8 : 2 = 4
Example 2. The number 3 is a divisor of 9 because 9 is divisible by 3 without a remainder:
9 : 3 = 3
Example 3. The number 4 is not a divisor of 10 because 10 is not divisible by 4 without a remainder:
10 : 4 = 2 (2 in the remainder)
Page 8 of 9