Now let's learn how to subtract fractions with different denominators. When fractions are subtracted, their denominators should be the same. But they are not always the same.
For example, you can subtract ![]() from fraction
from fraction ![]() because these fractions have the same denominators. But you cannot subtract
because these fractions have the same denominators. But you cannot subtract ![]() from fraction
from fraction ![]() because these fractions have different denominators. In such cases, the fractions must be reduced to the same (common) denominator.
because these fractions have different denominators. In such cases, the fractions must be reduced to the same (common) denominator.
The common denominator is found using the same principle we used when adding fractions with different denominators. First, we find the LCM of the denominators of both fractions. Then we divide the LCM by the denominator of the first fraction and obtain the first additional multiplier, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction to obtain the second additional multiplier, which is written over the second fraction.
The fractions are then multiplied by their additional multipliers. As a result of these operations, fractions with different denominators are converted to fractions with the same denominators. And we already know how to subtract such fractions.
Example 1. Find the value of the expression: 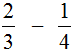
These fractions have different denominators, so you need to reduce them to the same (common) denominator.
First, find the LCM of the denominators of both fractions. The denominator of the first fraction is number 3, and the denominator of the second fraction is number 4. The least common multiple of these numbers is 12
LCM (3 and 4) = 12
Now back to fractions ![]() and
and ![]()
Find the additional factor for the first fraction. To do this, divide the LCM by the denominator of the first fraction. LCM is 12, and the denominator of the first fraction is 3. We divide 12 by 3 and get 4. Write the four above the first fraction:
![]()
Do the same with the second fraction. Divide the LCM by the denominator of the second fraction. LCM is 12, and the denominator of the second fraction is 4. Divide 12 by 4, and we get 3. Write the three above the second fraction:
![]()
Now we are ready for subtraction. It remains to multiply the fractions by their additional multipliers:
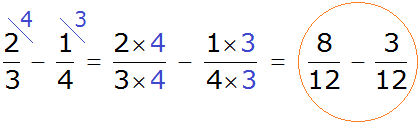
We found that fractions with different denominators turned into fractions with the same denominators. And we already know how to subtract such fractions. Let's solve this example to the end:
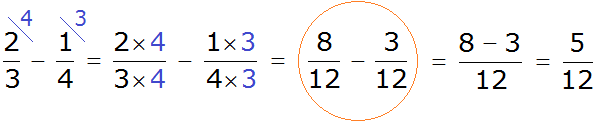
We got the answer.![]()
Let's try to represent our solution with a picture. If you cut off ![]() of a pizza from
of a pizza from ![]() pizza, you get
pizza, you get ![]() of a pizza
of a pizza
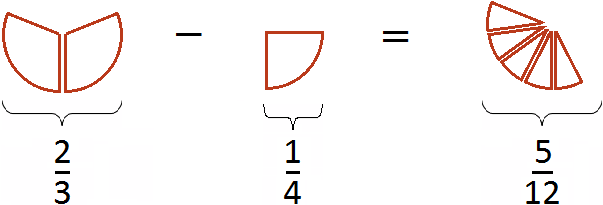
This is the detailed version of the solution. If we were in school, we would have to solve this example in a shorter form. The solution would look like this:
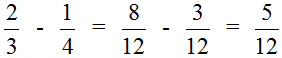
Fraction reduction ![]() and
and ![]() to a common denominator can also be represented using the figure. By reducing these fractions to a common denominator, we obtained fractions
to a common denominator can also be represented using the figure. By reducing these fractions to a common denominator, we obtained fractions ![]() and
and ![]() . These fractions will be represented by the same pieces of pizza, but this time they will be divided into the same fractions (reduced to the same denominator):
. These fractions will be represented by the same pieces of pizza, but this time they will be divided into the same fractions (reduced to the same denominator):
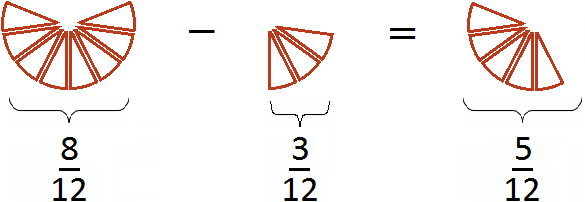
The first figure depicts a fraction![]() (eight pieces out of twelve), and the second drawing is a fraction
(eight pieces out of twelve), and the second drawing is a fraction ![]() (three slices out of twelve). By cutting off three slices from eight slices we get five slices from twelve. Fraction
(three slices out of twelve). By cutting off three slices from eight slices we get five slices from twelve. Fraction ![]() and describes these five pieces.
and describes these five pieces.
Example 2. Find the value of the expression 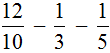
These fractions have different denominators, so we first need to reduce them to the same (common) denominator.
Find the LCM of the denominators of these fractions.
The denominators are 10, 3, and 5. The least common multiple of these numbers is 30
LCM (10, 3, 5) = 30
Now find the additional multipliers for each fraction. To do this, divide the LCM by the denominator of each fraction.
Find the additional factor for the first fraction. LCM is 30, and the denominator of the first fraction is 10. Divide 30 by 10, and we get the first additional factor 3. Write it over the first fraction:
![]()
Now find the additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is 30, and the denominator of the second fraction is 3. Dividing 30 by 3, we get the second additional factor 10. Write it over the second fraction:
![]()
Now find the additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is 30, and the denominator of the third fraction is 5. Divide 30 by 5, and we get the third additional factor 6. Write it over the third fraction:
![]()
Now everything is ready for subtraction. It remains to multiply the fractions by their additional multipliers:
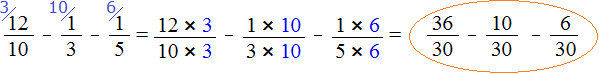
We found that fractions with different denominators turned into fractions with the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.
The continuation of the example won't fit on one line, so we move the continuation to the next line. Don't forget the equal sign (=) on the new line:
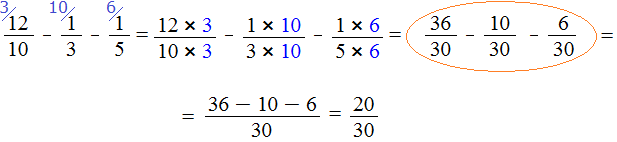
The answer is a correct fraction, and we seem to be fine with it, but it's too cumbersome and ugly. We should make it simpler. What can we do? We could shorten the fraction.
To reduce the fraction ![]() , divide its numerator and denominator by the greatest common divisor (GCD) of 20 and 30.
, divide its numerator and denominator by the greatest common divisor (GCD) of 20 and 30.
So, we find the GCD of numbers 20 and 30:
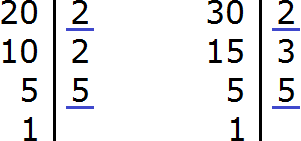
![]()
Now go back to our example and divide the numerator and denominator of the fraction ![]() by the found GCD, that is, by 10
by the found GCD, that is, by 10
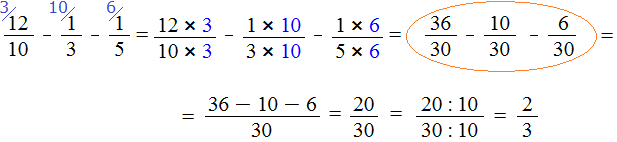
We got the answer ![]()
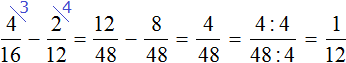
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.