Using variables

If an expression is complicated and you think it will confuse you as you solve a problem, you can put part of it into a variable, and then work with that variable.

Mathematicians often do this. They break a complex problem into easier subproblems and solve them. Then they assemble the solved subtasks into a single whole. This is a creative process, and it takes years of hard practice to learn.

The use of variables is justified when working with complex fractions. For example:

Find the value of the expression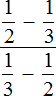  

So there is a fractional expression in the numerator and a fractional expression in the denominator. In other words, we are again faced with the complex fraction that we dislike so much.

The expression in the numerator can be written into a variable with any name, for example:

But in mathematics, in such a case, it is customary to name variables with large Latin letters. Let us not break this tradition, and denote the first expression by the capital Latin letter - A

And the expression in denominator can be denoted by the capital Latin letter - B

Now our original expression 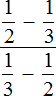takes the form . That is, we have replaced the numeric expression with a letter expression, having previously entered the numerator and denominator in the variables A and B.

Now we can separately calculate the values of variable A and the value of variable B. We insert the finished values into the expression .

Let us find the value of variable A

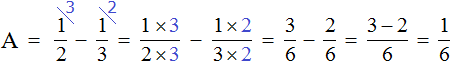
Let's find the value of variable B

Now substitute their values into the main expression instead of variables A and B:

We got a complex fraction in which we can use the scheme "from the first to the fourth, from the second to the third", that is, the figure that is on the first "level" to raise to the fourth "level", and the figure that is on the second "level" to raise to the third "level". Further calculation is not too difficult:

Thus, the value of the expression 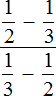is -1.

Of course, we looked at the simplest example, but our goal was to see how we could use variables to make things easier for ourselves, so that we could minimize errors.

Note also that the solution to this example can be written without using variables. It would look like this

This solution is faster and shorter, and in this case it would be better to write it that way, but if an expression turns out to be complex, consisting of several parameters, brackets, roots, and powers, it is advisable to calculate it in several steps, putting some of its expressions into variables.

Video lesson

Add comment