Definition. In simple terms, a fraction is a part of something. This "something" can be anything - food, money, a number. The word "fraction" also speaks for itself - it means a division.
Let's look at an example from life. We bought a pizza to eat during the day. Let's say we decide to divide it into four pieces so that we eat one piece at a time.
Look at this picture. Imagine that this is our pizza divided into four slices. Each slice of pizza is a fraction, because each slice individually is part of the pizza.
Let's say we ate one slice. How do we write it down? First a little line is drawn:
The bottom of this line records how many slices the pizza was divided into. The pizza was divided into four slices. So at the bottom of the line you write four:
And on top of this line is written how many pieces of pizza were eaten. One slice was eaten, so at the top of this line we write one:
These constructions are called fractions. A fraction consists of a numerator and a denominator.
The number that is written on top is called the numerator of the fraction.
The number that is written at the bottom is called the denominator of the fraction.
In this example, the numerator of the fraction is one and the denominator of the fraction is a four. This fraction can be read as "one fourth" or "one-fourth fraction" or "one-quarter" - all of which are synonyms.
Now imagine that we ate another slice of the same pizza, which was divided into four slices. How do we write down such a fraction?
Very simple. At the top, we write 2 (since two slices have been eaten), and at the bottom, we write 4 (since there were four slices total):
This fraction reads "two fourths" or "two fourths of a fraction".
Now imagine that we didn't divide the pizza into four pieces, but into three.
Suppose we ate one slice of this pizza. How do we write down a fraction like that?
Very simple. Again a small line is drawn. At the bottom of this line we write the number 3, because the pizza is divided into three parts, and at the top of this line we write the number 1, because we ate one slice:
This fraction reads like this: "One third" or "One slice of three" or "One-third share".
If we eat two slices of pizza, this fraction is called "two thirds" and is written as follows:
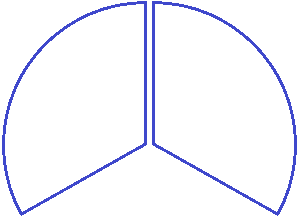
Now imagine that we have divided the pizza into two parts, or as they say popularly: "In half":
Suppose we ate one of the two slices. How do we write down such a fraction?
Again we draw a line. At the bottom of this line we write the number 2, because the pizza is divided into two pieces, and at the top we write the number 1, because one piece was eaten:
This fraction reads "one half" or "one half fraction".
The slices we have now considered are called the fractions.
Definition. In general, there are two kinds of fractions: the regular fractions and decimal fractions. At this point we are looking at regular fractions. An ordinary fraction is a fraction that consists of a numerator and a denominator. We will look at decimal fractions a little later.
The denominator of a fraction is a number that shows how many equal parts something can be divided into. Let's go back to our pizza. This pizza can be divided equally into 2 parts, 3 parts, 4 parts, 5 parts, and 6 parts. Depending on how many parts we divide the pizza into, the denominator will change.
The following figure shows three pizzas that are divided differently. The first pizza has a denominator of 2. The second pizza has a denominator of 3. The third pizza has a denominator of 4.
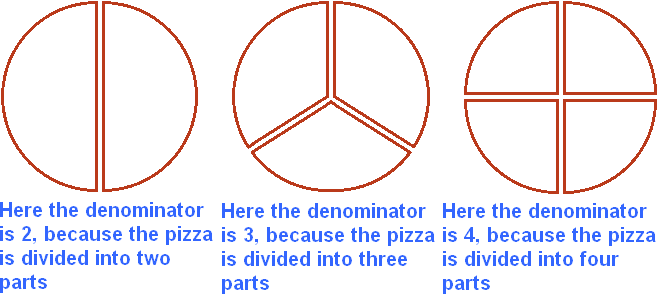
The numerator shows how many parts are taken from something. For example, if we divide a pizza into two parts, as in the first picture, and take one part for the meal, we take 
(one part of two), or as they say "half" of the pizza.
Using variables, the fraction can be written as follows:
where a - is the numerator and b - is the denominator.
Definition.The next thing that is important to know is that fractions can be proper and improper.
A proper fraction is a fraction whose numerator is smaller than the denominator. For example, the following fractions are proper:
Why are these fractions called proper fractions? Recall that a fraction is a part of something. After all, it makes more sense if the fraction is smaller than where the fraction was taken from. For example, if the pizza is divided into four parts, and we take 
(one fourth), then our slice will be smaller than all four slices combined (than one whole pizza). This is why such fractions are called proper fractions.
With an improper fraction, it's exactly the opposite. An improper fraction is a fraction where the numerator is larger than the denominator. For example, the following fractions are improper:
You can see that these fractions have a numerator greater than the denominator. Why are these fractions called improper fractions? Recall that a fraction is a part of something. The denominator shows how many parts of something are divided into. The numerator shows how much of something was taken.
Now take the improper fraction 
for example and apply it to our pizza. The denominator is 2, so the pizza is divided into two pieces, and the numerator is 9. So we took nine slices out of two. But how can you take nine slices if there are only two? The answer is no way. Therefore, such fractions are called improper fractions.
Fractions where the numerator and denominator are the same are also called improper. For example:
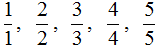
In general, such fractions should not even be called fractions. And here's why. Consider, for example, the fraction 
. Apply it to our pizza.
Let's say we want to eat pizzas. The denominator is 2, so the pizza is divided into two parts. And in the numerator is 2, so two parts are taken. In fact, the whole pizza is taken, and if we eat this pizza, we are not eating part of the pizza, but the whole pizza. In other words, eat not a fraction, but a whole fraction of a pizza. Therefore, a fraction with the same numerator and denominator is called an improper fraction.
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.