Here are short articles answering one specific question.
Sometimes it is convenient to show something in fractional form. For example, one tenth of a decimeter is written like this:
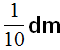
This expression means that one decimeter was divided into ten equal parts, and one part was taken from those ten parts. And one part of ten in this case is equal to one centimeter:
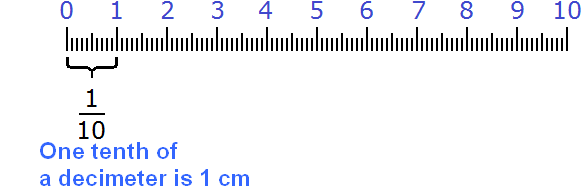
Consider the following example. Suppose we need to show 6 cm and another 3 mm in centimeters in fractional form.
So we already have 6 whole centimeters:

But there are still 3 millimeters left. How do you show these 3 millimeters in centimeters? Fractions come to the rescue. One centimeter is ten millimeters. Three millimeters is three parts of ten. And three parts of ten are written as ![]() cm
cm
The expression ![]() cm means that one centimeter was divided into ten equal parts, and three parts were taken from these ten parts.
cm means that one centimeter was divided into ten equal parts, and three parts were taken from these ten parts.
The result is six whole centimeters and three tenths of a centimeter:
![]()
The number 6 indicates the number of whole centimeters, and the fraction ![]() indicates the number of fractions. This fraction reads "six whole and three tenths centimeters".
indicates the number of fractions. This fraction reads "six whole and three tenths centimeters".
Fractions with numbers 10, 100, 1000 in the denominator can be written without a denominator. First write the whole part and then the numerator of the fractional part. The whole part is separated from the numerator of the fractional part by a decimal point.
For example, write down ![]() without the denominator. First we write down the whole part. The whole part is 6
without the denominator. First we write down the whole part. The whole part is 6
At the beginning of this lesson it was said that a divisor is a number by which another number is divisible without a remainder.
For example, number 2 is the divisor of number 6 because number 6 can be divided by 2 without a remainder
6 : 2 = 3
Another divisor of number 6 is number 3
6 : 3 = 2
Another divisor of number 6 is number 1
6 : 1 = 6
Finally, the divisor of number 6 is the number itself
6 : 6 = 1
List all the divisors of number 6
If you know the percentage of a number, you can find out the whole number.
For example, a business paid us $60000 for a job, and that is 2% of the total profit the business made. Knowing our share, and how much percentage it is, we can find out the total profit.
First you need to find out how many dollars is one percent. How to do it? Try to guess by carefully studying the following picture:
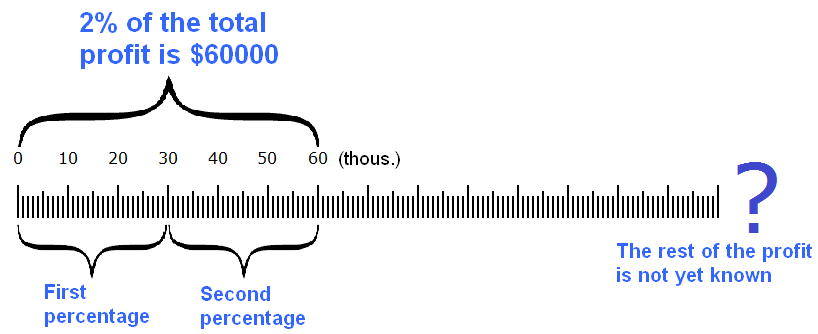
If 2 % of the total profit is $60,000, then it's easy to guess that one percent is $30,000. And to get that $30,000, you have to divide $60,000 by two.
60 000 : 2 = 30 000
We found one percent of the total profit, i.e., ![]() . If one part is 30 thousand, then to determine one hundred parts, you must multiply 30 thousand by 100
. If one part is 30 thousand, then to determine one hundred parts, you must multiply 30 thousand by 100
30 000 × 100 = 3 000 000
We found out the total profit. It is three million.
To find the whole number by its fraction, we divide the number by the numerator of the fraction and multiply the result by the denominator of the fraction.
For example, knowing that ![]() of the tape measure is 12 cm, we can find the length of the entire tape measure. To do this, divide 12 by 2, and multiply the result by 3.
of the tape measure is 12 cm, we can find the length of the entire tape measure. To do this, divide 12 by 2, and multiply the result by 3.
12 : 2 = 6
6 × 3 = 18
We got 18. So the length of the whole tape measure is 18 cm.
The rule of finding a percentage is the same as finding a fraction of a number.
To find the percentage of something, divide it by 100 parts and multiply the resulting number by the desired percentage.
For example, find 2% of 10 cm.
What does the entry 2% mean ? The entry 2% replaces the entry ![]() . If we translate this assignment into more comprehensible language, it would look like this:
. If we translate this assignment into more comprehensible language, it would look like this:
Find ![]() of 10 cm
of 10 cm
And we already know how to solve such problems. To find a fraction of a number, divide the number by the denominator of the fraction, and multiply the result by the numerator of the fraction.
Knowing part of a number and how much of it is from a whole number, you can find the original whole number. This is the inverse of the problem we looked at in the previous topic. There, we searched for the fraction of a number by dividing the number by the denominator of the fraction, and multiplying the result by the numerator of the fraction.
Now, on the contrary, knowing the fraction and how much it is of the number, we need to find the original whole number.
For example, if ![]() of the length of a ruler is six centimeters and we are told to find the length of the entire ruler, we should understand that we are required to find the original whole (the length of the entire ruler) by the fraction
of the length of a ruler is six centimeters and we are told to find the length of the entire ruler, we should understand that we are required to find the original whole (the length of the entire ruler) by the fraction ![]() . Let's solve this problem.
. Let's solve this problem.
To find a fraction of a number, we divide the number by the denominator of the fraction and multiply the result by the numerator of the fraction.
For example, to find ![]() of 10 centimeters, you need to divide 10 by 5, and multiply the result by 2.
of 10 centimeters, you need to divide 10 by 5, and multiply the result by 2.
10 : 5 = 2
2 × 2 = 4
The answer is 4. So ![]() of ten centimeters is 4 centimeters. Schematically it looks like this:
of ten centimeters is 4 centimeters. Schematically it looks like this:
Definition. The greatest common divisor (or greatest common factor) of a and b is the greatest number by which a and b are both divided without a remainder.
To understand this definition well, substitute any two numbers instead of variables a and b. For example, instead of the variable a we use the number 12, and instead of the variable b we use the number 9. Now let's try to read this definition:
The greatest common divisor of 12 and 9 is the greatest number by which 12 and 9 are divided without a remainder..
It is clear from the definition that we are talking about the common divisor of the numbers 12 and 9. The divisor is the greatest of all existing divisors. This greatest common divisor (GCD) must be found.
There are three ways to find the greatest common divisor of two numbers. The first way is quite time consuming, but it gives you a good understanding of the subject and a sense of its meaning.
The second and third ways are quite simple and allow you to quickly find the GCD. Consider all three methods. It is up to you to choose which one to use in practice.
The first way is to find all possible divisors of two numbers and to choose the greatest of them. Consider this method for the following example: find the greatest common divisor of 12 and 9.
We already said that a fraction is a part of something. That part can be anything. For example, ![]() of a pizza is a half of a pizza:
of a pizza is a half of a pizza:

But the usage of fractions does not end with one pizza. For example, you can find out how much is ![]() of ten centimeters:
of ten centimeters:
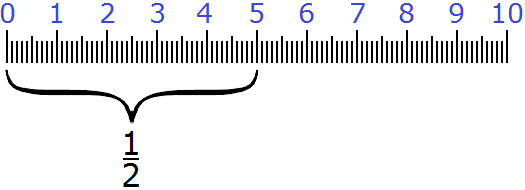
As you have already guessed, ![]() of ten centimeters is five centimeters. After all,
of ten centimeters is five centimeters. After all, ![]() is the simplest fraction, which means half of something. We had ten centimeters. We divided those ten centimeters in half and got five centimeters.
is the simplest fraction, which means half of something. We had ten centimeters. We divided those ten centimeters in half and got five centimeters.
To reduce the fractions to a common denominator, we have to find the LCM (least common multiple) of the denominators of these fractions. Then we need to divide the found LCM by the denominator of the first fraction and obtain an additional multiplier for the first fraction.
We do the same for the second fraction - we divide the LCM by the denominator of the second fraction and get an additional multiplier for the second fraction.
Then the fractions are multiplied by their additional multipliers. As a result, they are converted into fractions with the same denominators.
For example, the expression ![]() is calculated as follows:
is calculated as follows:
Long addition
 Definition. Long addition is a math operation for adding numbers together. Adding in columns is done by digits - ones are added to ones, tens to tens, hundreds to hundreds, thousands to thousands.
Definition. Long addition is a math operation for adding numbers together. Adding in columns is done by digits - ones are added to ones, tens to tens, hundreds to hundreds, thousands to thousands.
Let us have a few examples.
Example 1. Add 61 and 23.
Write first the first number and then the second number, so that the ones and tens of the second number are under the ones and tens of the first number. Write all this with the addition sign (+) vertically:
Page 5 of 9