To reduce the fractions to a common denominator, we have to find the LCM (least common multiple) of the denominators of these fractions. Then we need to divide the found LCM by the denominator of the first fraction and obtain an additional multiplier for the first fraction.
We do the same for the second fraction - we divide the LCM by the denominator of the second fraction and get an additional multiplier for the second fraction.
Then the fractions are multiplied by their additional multipliers. As a result, they are converted into fractions with the same denominators.
For example, the expression ![]() is calculated as follows:
is calculated as follows:
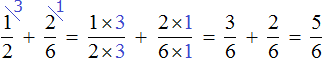
But there is another way to reduce fractions to a common denominator. This method is often used by schoolchildren and lazy students. The essence of this method is that the role of additional multipliers is taken by the denominators of both fractions, and it happens "crosswise" - the denominator of the first fraction becomes an additional multiplier of the second fraction, and the denominator of the second fraction becomes an additional multiplier of the first fraction.
Calculate the previous expression ![]() this way. The denominator of the first fraction 2 becomes an additional factor of the second fraction, and the denominator of the second fraction 6 becomes an additional factor of the first fraction:
this way. The denominator of the first fraction 2 becomes an additional factor of the second fraction, and the denominator of the second fraction 6 becomes an additional factor of the first fraction:
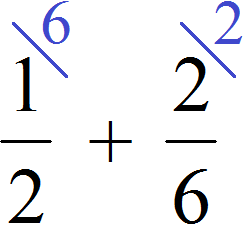
Then multiply the numerator and denominator of each fraction by its additional multiplier and calculate:
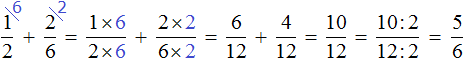
The advantage of this method is that it is not necessary to find the LCM of the denominators of both fractions. In the process of calculation, everything aligns itself. The only disadvantage is that the expression becomes longer and sloppier.
Compare the expressions that we calculated first by the first method and then by the second method:
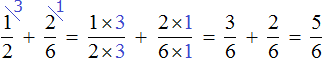
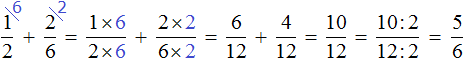
An expression calculated by the first method is much neater and shorter than the second.
We will use the second method when studying algebra. In algebra we have to work with letter expressions more often than with number expressions.
For example, if we are to reduce the alphabetic expression ![]() to a common denominator, we will have no choice but to use the "crosswise" method, that is, the second method, which we have just considered:
to a common denominator, we will have no choice but to use the "crosswise" method, that is, the second method, which we have just considered:
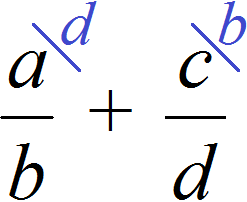
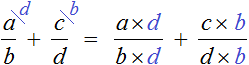
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.