Long subtraction
Example 1. Subtract number 53 from number 69.
Write down the numbers in columns. Units under ones, tens under tens. Then subtract by digits. Subtract the units of the first number from the units of the second number. Subtract the tens of the first number from the tens of the second number:
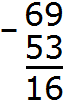
We got the answer 16.
Example 2. Find the value of the expression 95 - 26
Write the expression in columns:
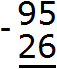
The units digit of 95 contains 5 units, and the units digit of 26 contains 6 units. Six units cannot be subtracted from five units, so we take one tenth from the digit of tens. This tens and the five available units together make 15 units. From 15 units we can subtract 6 units, which makes 9 units. Write the number 9 in the units division of our answer:
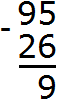
Now subtract the tens. The range of tens of the number 95 used to contain 9 tens, but we took from this range one tens, and now it contains 8 tens. And the range of tens of the number 26 contains two tens. Two tens can be subtracted from eight tens to make six tens. Write the number 6 in the tens digit of our answer:
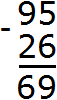
Let's use an unconventional subtraction method in which each digit included in the number is treated as a separate number. When subtracting large numbers in columns, this method is very convenient.
The number 5 is in the order of the units of the subtractor. The number 6 is in the order of the units of the subtractor. So we take one unit from number 9. The taken unit is mentally added to the left of the five. And since we took one unit from number 9, the number will be reduced by one unit:
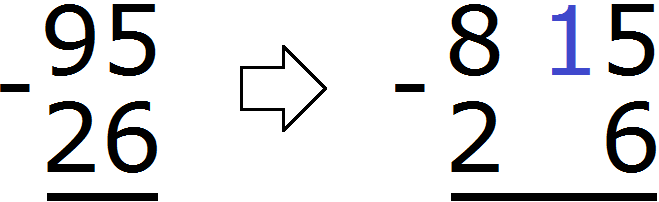
As a result, five turns into 15. Now you can subtract 6 from 15. You get 9. Write 9 in the units division of our answer:
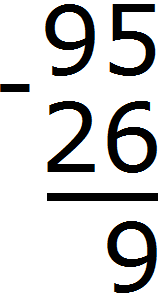
Let's go to the number of tens. The number 9 used to be there, but because we took one unit from it, it turned into number 8. In the tens division of the second number is the number 2. Eight minus two is six. Write number 6 in the decimal place of our answer:
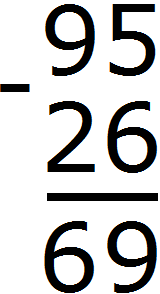
Example 3. Find the value of the expression 2412 - 2317
Write down this expression in the column:
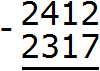
The number 2 is in the unit digit of 2412, and the number 7 is in the unit digit of 2317. You can't subtract a seven from a two, so we take one from the next number 1. We mentally add the taken one to the left of the two:
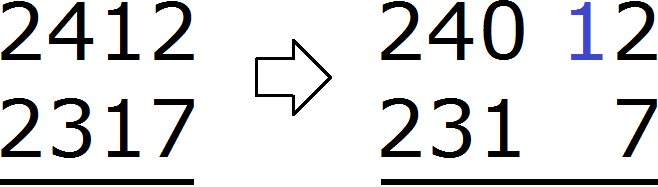
As a result, the two converts to the number 12. Now you can subtract 7 from 12. You get 5. Write the number 5 in the units division of our answer:
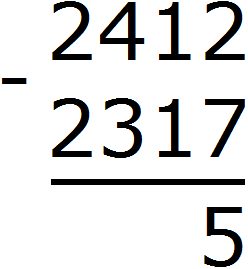
Let's move on to tens. In the range of tens of 2412 there was previously a number 1, but because we took from it one unit, it turned into 0. And in the range of tens of 2317 there is a number 1. From zero you cannot subtract one. So we take one from the next number 4. We mentally add one to the left of zero. And since we took one unit from number 4, the number will decrease by one:
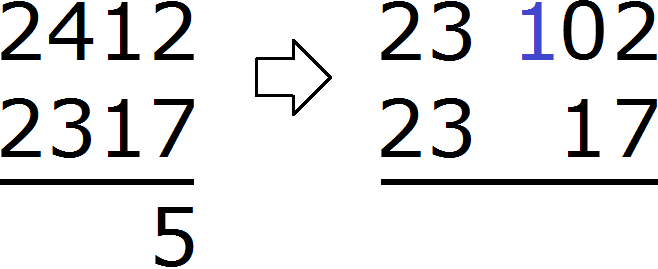
As a result, zero is converted to 10. Now you can subtract 1 from 10. You get 9. Write 9 in the decimal place of our answer:
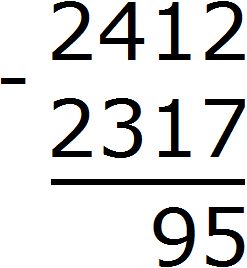
The hundredths digit of 2412 used to contain the number 4, but now it contains the number 3. The hundredths digit of 2317 also has the number 3. Three minus three equals zero. It's the same with the bits of thousands in both numbers. Two minus two equals zero. And if the difference of the higher digits equals zero, then this zero is not written down. Therefore, the final answer is number 95.
Example 4. Find the value of the expression 600 - 8
Let's write the expression in columns:
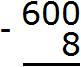
The unit digit of 600 contains zero, and the unit digit of 8 contains the number itself. You can't subtract an eight from zero, so we take one from the next number. But the next number is also zero. Then for the next number we take the number 60. We take one from that number and mentally add it to the left of zero. And since we took one unit from number 60, that number will decrease by one unit:

Now the number 10 is in the ones place. You can subtract 8 from 10 to get 2. Write the number 2 in the units place of the new number:
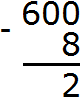
Move on to the next number, which is in the range of tens. In the range of tens used to be zero, but now there is a number 9, and in the second number the range of tens is absent. Therefore, the number 9 is moved to the new number:
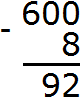
Move on to the next number, which is in the range of hundreds. In the range of hundreds there used to be number 6, but now there is number 5, and in the second number the range of hundreds is absent. Therefore, the number 5 is transferred to the new number:
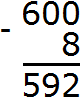
Example 5. Find the value of the expression 10000 - 999
Write the expression in the column:
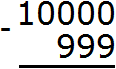
In the units digit of 10000 there is a 0, and in the units digit of 999 there is a 9. You cannot subtract a nine from a zero, so we take one from the next number in the tens division. But the next digit is also zero. Then we take 1000 as the next number and take one from that number:
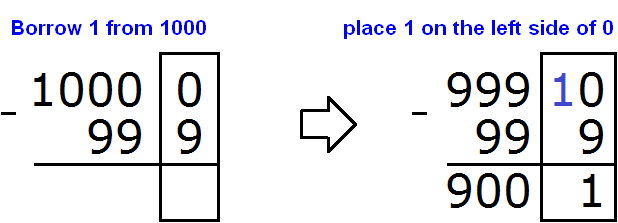
The next number in this case was 1000. By taking one from it, we converted it to 999. We added the one we took to the left of the zero.
Further calculation was not too difficult. Ten minus nine equaled one. Subtraction of the numbers in the tens division of both numbers gave zero. Subtracting the numbers in the hundred division of both numbers also yielded zero. And the nine in the thousands division was transferred to the new number:
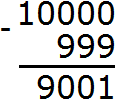
Example 6: Find the value of the expression 12301 - 9046
Let's write the expression in the column:
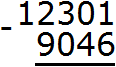
The unit digit of 12301 contains the number 1, and the unit digit of 9046 contains the number 6. Six cannot be subtracted from one, so we take one from the next number in the tens digit. But in the next digit is zero. Zero can not give us anything. Then for the next number we take 1230 and take one from it:
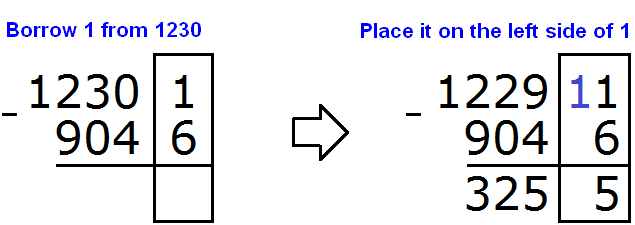
The next number in this case was 1230. By taking one from it, we converted it to 1229. And we mentally added the taken unit to the left of the unit in the division of units.
The further calculation was not difficult. Eleven minus six equaled five. Subtracting the numbers in the tens order of both numbers gave the number five. Subtracting numbers in the hundredths order of both numbers gave the number 2. Subtracting the numbers in the thousands division of both numbers gave the number 3.

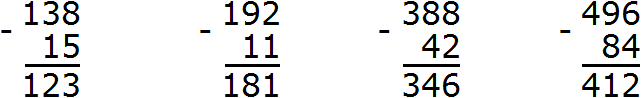
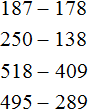

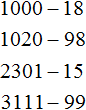
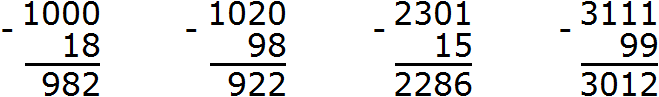
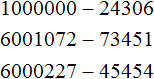
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.