Knowing part of a number and how much of it is from a whole number, you can find the original whole number. This is the inverse of the problem we looked at in the previous topic. There, we searched for the fraction of a number by dividing the number by the denominator of the fraction, and multiplying the result by the numerator of the fraction.
Now, on the contrary, knowing the fraction and how much it is of the number, we need to find the original whole number.
For example, if 
of the length of a ruler is six centimeters and we are told to find the length of the entire ruler, we should understand that we are required to find the original whole (the length of the entire ruler) by the fraction . Let's solve this problem.
Find the length of the whole ruler by the fraction . It is known that of the length of the whole ruler is 6 cm.
We already know how we got the 6 cm. There was some length, and it was divided into five parts, because the denominator of the fraction is the number 5. Then two parts of the five parts were taken because the numerator of the fraction is number 2.
To know the length of the whole ruler, you first need to know the length of one part. How do we find this out? Let's try to guess by looking closely at the following picture:
If two parts of the length of the ruler are 6 cm, then it is easy to guess that one part is 3 cm. And to get those 3 cm, you have to divide 6 by 2.
6 cm : 2 = 3 cm
So we found the length of one part. One part of five, or 
of the length of a ruler, is 3 cm. If there are only five parts, then to find the length of the ruler, you have to take three centimeters five times. In other words, multiply 3 cm by the number 5
3 cm × 5 = 15
We found the length of the ruler. It is 15 centimeters. This can be seen in the following picture.
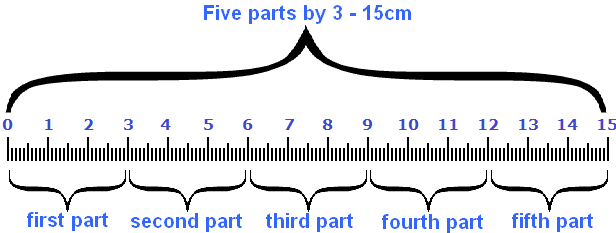
You can see that five parts of five or 
make fifteen centimeters.
To make it easier to find a number by its fraction, you can use the following rule:
To find a number by its fraction, you need to divide the known number by the numerator of the fraction, and multiply the result by the denominator of the fraction.
Example 2. The number 20 is 
of the whole number. Find this number.
The denominator of the fraction shows that the number we need to find is divided into five parts. If of that number is 20, then to find the whole number, we must first find (one part of five) of the whole number. To do this, 20 must be divided by the numerator of the fraction
20 : 4 = 5
We found of the whole number. That fraction is 5. To find the whole number, multiply the result of 5 by the denominator of the fraction
5 × 5 = 25
We found of the whole number. In other words, we found the whole number we were asked to find. That number is 25.
Example 3. Ten minutes is 
of the cooking time of the porridge. Find the total cooking time of the porridge.
The denominator of the fraction shows that the total cooking time of the porridge is divided into three parts. If of the cooking time is ten minutes, then to find the total cooking time, you must first find 
of the cooking time. To do this, divide 10 by the numerator of fraction
10 min : 2 = 5 min
We found of the porridge cooking time. of the porridge cooking time is five minutes. To find the total cooking time, multiply 5 minutes by the denominator of the fraction 
5 min × 3 = 15 min
We found 
of the cooking time of the porridge, that is, we found the total cooking time. It is 15 minutes.
Example 4. 
of the mass of a sack of cement is 30 kg. Find the total mass of the sack.
The denominator of the fraction shows that the total mass of the sack is divided into four parts. If the mass of the sack is 30 kg, then in order to find the total mass of the sack you must first find 
of the mass of the sack. To do this, divide 30 by the numerator of the fraction .
30kg : 2 = 15kg
We found of the mass of the sack. The mass of the sack is 15 kg. Now to find the total mass of the sack, multiply 15kg by the denominator of the fraction
15kg × 4 = 60kg
We found the 
mass of the sack. In other words, we found the total mass of the sack. The total mass of the sack of cement is 60 kg.
Exercises
of this number is 16.8 × 3 = 24
of this number is 32.32 × 2 = 64
of this number is 150.30 × 8 = 240
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.