At the beginning of this lesson it was said that a divisor is a number by which another number is divisible without a remainder.
For example, number 2 is the divisor of number 6 because number 6 can be divided by 2 without a remainder
6 : 2 = 3
Another divisor of number 6 is number 3
6 : 3 = 2
Another divisor of number 6 is number 1
6 : 1 = 6
Finally, the divisor of number 6 is the number itself
6 : 6 = 1
List all the divisors of number 6
1, 2, 3, 6
Sometimes you need to find all the divisors of a number. To understand how to do this, let's look at some examples.
Example 1. Find the divisors of number 12
First, one is a divisor of any number. Let us also have the first divisor of 12 be 1.
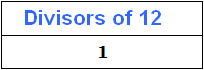
Now decompose the number 12 into prime factors:

We obtained the decomposition 2 × 2 × 3.
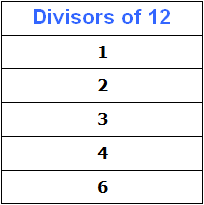
In the process of decomposition of number 12 into prime factors, we divided it into numbers 2 and 3. They divided number 12 without a remainder, so they are also divisors of number 12. Let's add these two numbers to our table of divisors:

To get the remaining divisors of number 12, you need to find all possible products of its prime factors among themselves. The resulting answers will be the remaining divisors of number 12.
We have decomposed number 12 into prime factors 2 × 2 × 3. Find all possible products of these prime factors among themselves. The first product is 2 × 2. This product is equal to 4
2 × 2 = 4
Let's put number 4 in our table of divisors

The next possible product of prime factors of number 12 is the product of 2 × 3. This product is 6. Let's put the number 6 in our table of divisors:
The last possible product of prime factors of number 12 is the product of all its factors, namely 2 × 2 × 3. This product is 12. Let's put the number 12 in our table of divisors:
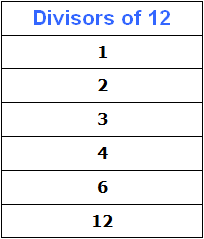
Thus, the divisors of number 12 are 1, 2, 3, 4, 6, 12.
Based on this example, we can form a rule for finding the divisors of a number:
To find the divisors of a number, you need to:
- write 1 as the first divisor;
- Decompose the original number into prime factors and write out of the resulting prime factors that are divisors of the original number (if a factor repeats, then write it out only once);
- find all possible products of obtained prime factors among themselves. The resulting answers will be the remaining divisors of the original number.
Example 2. Find the divisors of number 6
Write one as the first divisor of number 6:
1
Now decompose the number 6 into prime factors:
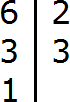
Write out from the resulting expansion those multipliers that are divisors of number 6. We see that these are multipliers 2 and 3. They will be the next divisors of number 6. Let's add them to our divisors:
1, 2, 3
Now find all possible products of prime factors of number 6. In this case, there is only one product, namely 2 × 3. This product is 6. Add 6 to our divisors:
1, 2, 3, 6
Thus, the divisors of number 6 are the numbers 1, 2, 3, 6.
Comments