When you need to divide a large number, it is a must to use this method.
Before long division, you must know:
- normal division of small numbers;
- division with a remainder;
- long multiplication;
- long subtraction.
Let's look at the long division with a simple example. Let us find the value of the expression 9 : 3. The long division is written as follows:
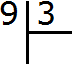
Example 1. Everyone knows that nine divided by three is three. The answer (quotient) is written like this:
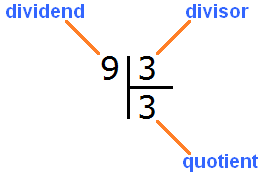
To check if there is a remainder of division, you need to multiply the quotient by the divisor and write the answer under the quotient. The quotient in this case is 3, and the divisor is also 3. Multiply these two numbers: 3 x 3 = 9. This gives us 9. Write this nine under the divisor:
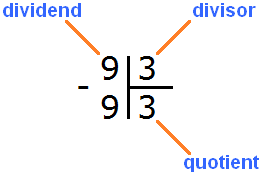
Now from the divisor we subtract the nine we wrote under it: 9 - 9 = 0. The remainder is zero. Simply put, there is no remainder. This completes the division successfully:
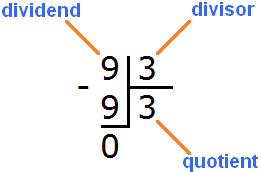
Example 2. Find the value of the expression 8 : 3
Eight times three is not a simple division. The multiplication table won't help either. In this case the remainder of division will be present.
Let's first write this expression with long divison:
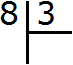
Now we have to ask the question, "How many threes are in an eight?" An eight contains two threes. This can even be seen firsthand if we think of an eight as eight sticks:
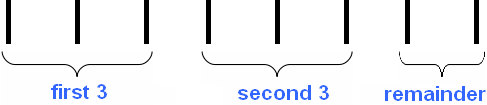
At school, the quotient is picked up by the matching method. We've all heard phrases like "take one," "take two," or "take three. We have just such a case. We take two by answering that there are two threes in an eight. We write the two in the right-hand corner:
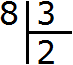
Now take out the remainder. To do this, multiply the quotient by the divisor (2 by 3) and write the resulting number under the divisor:
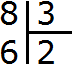
Then we subtract 6 from 8. The resulting number is the remainder:
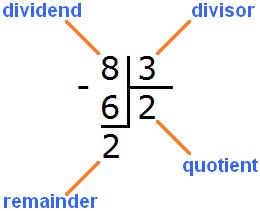
8 : 3 = 2 (2 in the remainder)
Check: (2 x 3) + 2 = 6 + 2 = 8
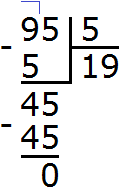
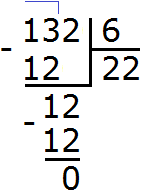
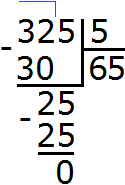
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.