From the previous lesson we know that if any number is divisible by another number without a remainder, it is called a multiple of that number.
It turns out that a multiple can be common to several numbers. And now we will be interested in the multiple of two numbers, and it should be as small as possible.
Definition. The least common multiple (LCM) of a and b is the smallest number that is a multiple of a and b. In other words, it is the smallest number that is divisible without a remainder by a and b.
The definition contains two variables a and b. Let's substitute any two numbers for these variables. For example, instead of variable a, let's substitute number 9, and instead of variable b, let's substitute number 12. Now let's try to read the definition:
The least common multiple (LCM) of 9 and 12 is the smallest number that is a multiple of 9 and 12. In other words, it is the smallest number that is divisible without a remainder by 9 and by 12..
From the definition it is clear that the smallest common multiple is the smallest number that is divisible without a remainder by 9 and by 12. This least common multiple must be found.
There are three ways to find the least common multiple (LCM). The first method is to write out the first multiples of two numbers, and then choose among those multiples a number that is common to both numbers and is small. Let's apply this method.
First, find the first multiples of 9. To find multiples of 9, multiply this nine by numbers from 1 to 9 one by one. The answers will be multiples of 9.
So, let's begin. The multiples will be highlighted in blue:
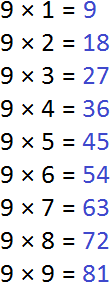
Now we find multiples for number 12. To do this, multiply the number 12 by all the numbers 1 to 12 in turn:
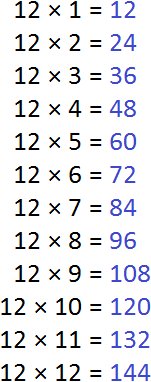
Now write out multiples of both numbers:
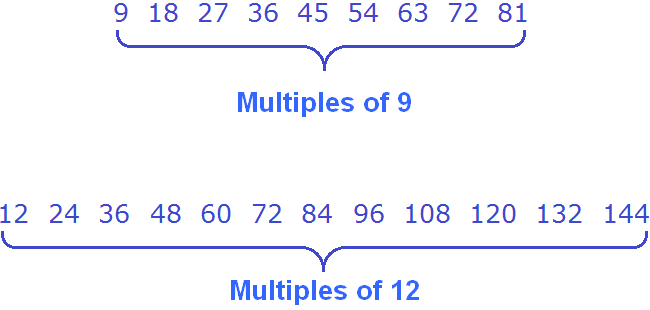
Now find the common multiples of both numbers. Once we find them, let's underline them at once:
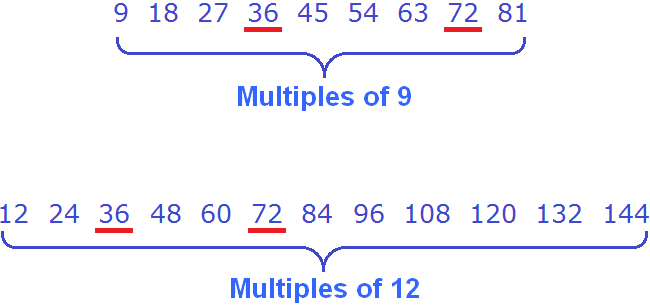
Common multiples of 9 and 12 are multiples of 36 and 72. The smallest of them is 36.
So the smallest common multiple of 9 and 12 is 36. This number is divisible by 9 and 12 without a remainder:
36 : 9 = 4
36 : 12 = 3
LCM (9 and 12) = 36
The second way to find the LCM
The second way is that the numbers for which we are looking for the least common multiple are decomposed into prime factors. Then write out the multipliers included in the first expansion, and add the missing multipliers from the second expansion. The resulting multipliers are multiplied and obtained LCM.
Let us apply this method to the previous problem. Find the LCM for numbers 9 and 12.
Decompose number 9 into factors

Decompose the number 12 into factors

Let us write out the first decomposition:
![]()
Now add the multipliers from the second expansion, which are absent in the first expansion. The first expansion does not contain two twos. We add them:
![]()
Now multiply these multipliers:
![]()
The answer is 36. So the least common multiple of 9 and 12 is 36. This number is divisible by 9 and 12 without a remainder:
36 : 9 = 4
36 : 12 = 3
LCM (9 and 12) = 36
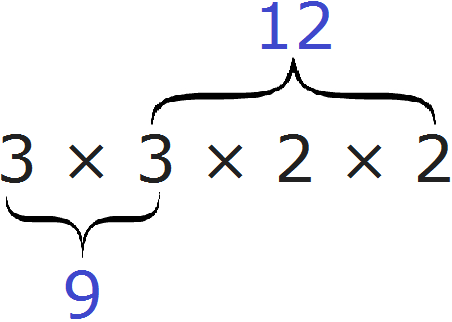
In simple terms, it all comes down to organizing a new decomposition with both decompositions at once. The decomposition of the first number 9 is the multipliers 3 and 3, and the decomposition of the second number 12 is the multipliers 2, 2 and 3.
Our task was to organize a new expansion which would include the expansion of number 9 and the expansion of number 12 at the same time. To do this, we wrote out the expansion of the first number and added to it the multipliers from the second expansion that were not in the first expansion. As a result, we got a new decomposition 3 × 3 × 2 × 2. It is easy to see that it includes the decomposition of 9 and the decomposition of 12
Example 2. Find the LCM of 50 and 180
Decompose the number 50 into factors
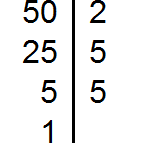
Decompose number 180 into factors

Let us write out the first decomposition:
![]()
Now add the multipliers from the second expansion, which are absent in the first expansion. The first expansion does not contain one more two and two threes. We add them:
![]()
Now multiply these multipliers:
![]()
The answer is 900. So the least common multiple of 50 and 180 is 900. This number is divisible by 50 and 180 without a remainder:
900 : 50 = 18
900 : 180 = 5
LCM (50 and 180) = 900
Example 3. Find the LCM of 8, 15, and 33
Decompose the number 8 into factors
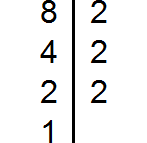
Decompose number 15 into factors
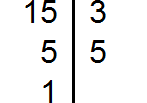
Decompose number 33 into factors
Let us write out the first decomposition:
![]()
Now add the factors from the second and third expansion, which are absent in the first expansion. Add the factors 3 and 5 from the second expansion, and the factor 11 from the third expansion:
![]()
Now multiply these multipliers:
![]()
The answer is 1320. So the least common multiple of 8, 15, and 33 is 1320. This number is divisible by 8, 15, and 33 without a remainder:
1320 : 8 = 165
1320 : 15 = 88
1320 : 33 = 40
LCM (8, 15and 33) = 1320
The third way to find the LCM
There is a third way to find the least common multiple. It works as long as it is searched for two numbers and as long as the greatest common divisor of those numbers is already found.
This method is more reasonable to use when you need to find the GCD and LCM of two numbers at the same time.
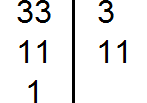
For example, let us find the GCD and LCM of the numbers 24 and 12. First, find the GCD of these numbers:
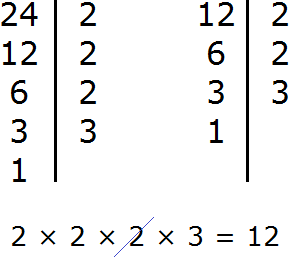
Now to find the least common multiple of 24 and 12, you need to multiply these two numbers and divide the result by their greatest common divisor.
So let's multiply the numbers 24 and 12
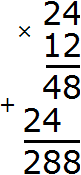
Divide the resulting number 288 by the GCD of numbers 24 and 12
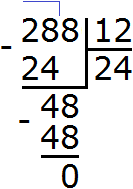
The answer is 24. So the least common multiple of 24 and 12 is 24.
LCM (24 and 12) = 24
Example 2. Find the GCD and LCM of 36 and 48
Find the GCD of 36 and 48
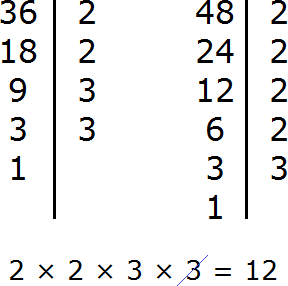
Multiply the numbers 36 and 48

Divide 1728 by the GCD of 36 and 48
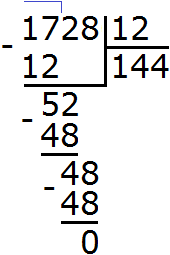
We got 144. So the least common multiple of 36 and 48 is 144.
LCM (36 and 48) = 144
To check, we can find the LCM by the usual second method we used before. If we have done everything correctly, we should get 144
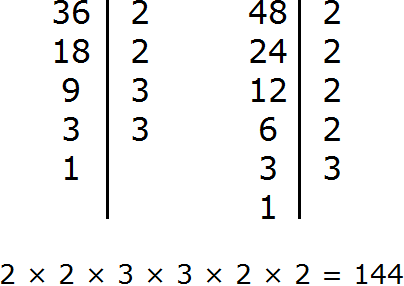
Don't get upset if you don't learn how to find GCD and LCM right away. The main thing is to understand what it is and how it works. And mistakes are quite natural at the beginning. As they say, "We learn by our mistakes.


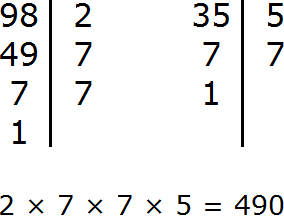
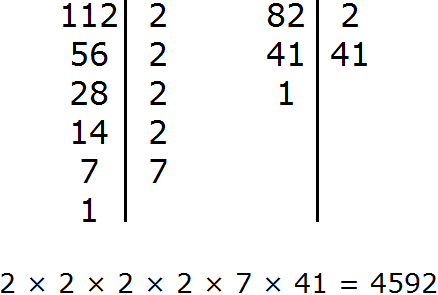
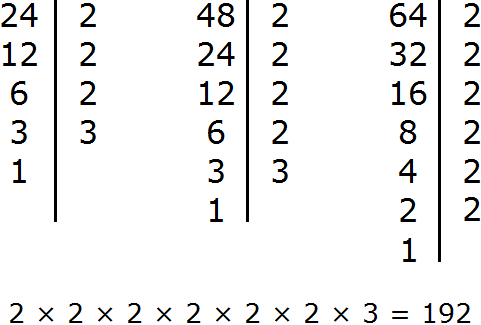
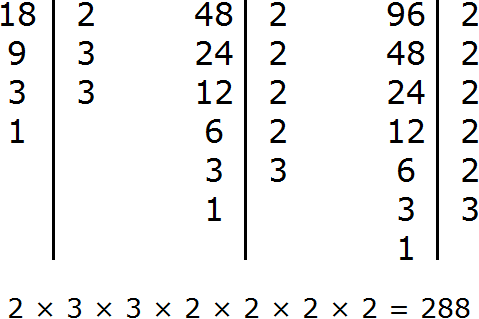
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.