Definition. The greatest common divisor (or greatest common factor) of a and b is the greatest number by which a and b are both divided without a remainder.
To understand this definition well, substitute any two numbers instead of variables a and b. For example, instead of the variable a we use the number 12, and instead of the variable b we use the number 9. Now let's try to read this definition:
The greatest common divisor of 12 and 9 is the greatest number by which 12 and 9 are divided without a remainder..
It is clear from the definition that we are talking about the common divisor of the numbers 12 and 9. The divisor is the greatest of all existing divisors. This greatest common divisor (GCD) must be found.
There are three ways to find the greatest common divisor of two numbers. The first way is quite time consuming, but it gives you a good understanding of the subject and a sense of its meaning.
The second and third ways are quite simple and allow you to quickly find the GCD. Consider all three methods. It is up to you to choose which one to use in practice.
The first way is to find all possible divisors of two numbers and to choose the greatest of them. Consider this method for the following example: find the greatest common divisor of 12 and 9.
First, find all possible divisors of 12. To do this, divide 12 by all the divisors between 1 and 12. If the divisor allows us to divide 12 without a remainder, we will highlight it in blue and make a corresponding explanation in parentheses.
12 : 1 = 12
(12 is divided by 1 without a remainder, so 1 is a divisor of 12.)
12 : 2 = 6
(12 divided by 2 without a remainder, so 2 is a divisor of 12.)
12 : 3 = 4
(12 divided by 3 without a remainder, so 3 is a divisor of 12.)
12 : 4 = 3
(12 divided by 4 without a remainder, so 4 is a divisor of 12.)
12 : 5 = 2 (2 in the remainder)
(12 is not divided by 5 without a remainder, so 5 is not a divisor of 12.)
12 : 6 = 2
(12 is divided by 6 without a remainder, so 6 is a divisor of 12.)
12 : 7 = 1 (5 in the remainder)
(12 is not divided by 7 without a remainder, so 7 is not a divisor of 12.)
12 : 8 = 1 (4 in the remainder)
(12 is not divided by 8 without a remainder, so 8 is not a divisor of 12.)
12 : 9 = 1 (3 in the remainder)
(12 is not divided by 9 without a remainder, so 9 is not a divisor of 12.)
12 : 10 = 1 (2 in the remainder)
(12 is not divided by 10 without a remainder, so 10 is not a divisor of 12.)
12 : 11 = 1 (1 in the remainder)
(12 is not divided by 11 without a remainder, so 11 is not a divisor of 12.)
12 : 12 = 1
(12 divided by 12 without a remainder, so 12 is a divisor of 12.)
Now let's find the divisors of 9. To do this, check all divisors from 1 to 9
9 : 1 = 9
(9 is divisible by 1 without a remainder, so 1 is a divisor of 9.)
9 : 2 = 4 (1 in the remainder)
(9 is not divided by 2 without a remainder, so 2 is not a divisor of 9.)
9 : 3 = 3
(9 is divisible by 3 without a remainder, so 3 is a divisor of 9.)
9 : 4 = 2 (1 in the remainder)
(9 is not divisible by 4 without a remainder, so 4 is not a divisor of 9.)
9 : 5 = 1 (4 in the remainder)
(9 is not divisible by 5 without a remainder, so 5 is not a divisor of 9.)
9 : 6 = 1 (3 in the remainder)
(9 is not divisible by 6 without a remainder, so 6 is not a divisor of 9.)
9 : 7 = 1 (2 in the remainder)
(9 is not divisible by 7 without a remainder, so 7 is not a divisor of 9.)
9 : 8 = 1 (1 in the remainder)
(9 is not divisible by 8 without a remainder, so 8 is not a divisor of 9.)
9 : 9 = 1
(9 is divisible by 9 without a remainder, so 9 is a divisor of 9.)
Now write down the divisors of both numbers. The numbers highlighted in blue are the divisors. Let's write them out:
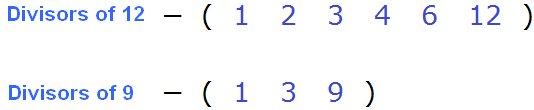
By writing out the divisors, you can immediately determine which is the largest and most common.
By definition, the greatest common divisor of 12 and 9 is the number by which 12 and 9 are divided without a remainder. The greatest and common divisor of 12 and 9 is the number 3
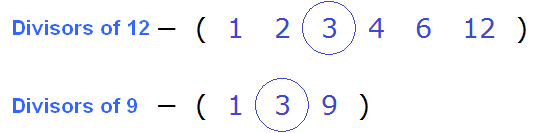
Both the number 12 and the number 9 are divided by 3 without a remainder:
12 : 3 = 4
9 : 3 = 3
So the GCD (12 and 9) = 3
The second way to find the GCD
Now consider the second method of finding the greatest common divisor. The essence of this method is to decompose both numbers into prime factors and multiply the common ones.
Example 1. Find the GCD of numbers 24 and 18
First, decompose both numbers into prime factors:
Now multiply their common multipliers. To avoid confusion, the common multipliers can be underlined.
Let's look at the decomposition of the number 24. Its first factor is 2. We look for the same factor in the expansion of 18 and we see that it is there too. Underline both twos:
Again we look at the decomposition of the number 24. Its second factor is also 2. Look for the same factor in the expansion of 18 and see that it is not there for the second time. Then we do not underline anything.
The next two in the expansion of 24 is also missing in the expansion of 18.
Move on to the last multiplier in the expansion of 24. We look for the same factor in the expansion of 18 and we see that it is there too. Underline both triples:
So, the common multipliers of 24 and 18 are multipliers 2 and 3. These multipliers must be multiplied to obtain the GCD:
2 × 3 = 6
So the GCD (24 and 18) = 6
The third way to find the GCD
Now consider the third method of finding the greatest common divisor. The essence of this method is that the numbers subject to the search for the greatest common divisor are decomposed into prime factors. Then from the expansion of the first number to cross out the multipliers that are not included in the expansion of the second number. The remaining numbers in the first expansion are multiplied and obtained GCD.
Example 1. Find the GCD of 28 and 16.
First, we decompose 28 and 16 into prime factors:
We got two decompositions: 
Now we remove from the expansion of the first number the multipliers that are not included in the expansion of the second number. The expansion of the second number does not include a seven. And we cross it out of the first expansion:
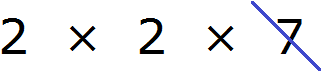
Now multiply the remaining multipliers and get the GCD:
The number 4 is the greatest common divisor of 28 and 16. Both of these numbers divide by 4 without a remainder:
28 : 4 = 7
16 : 4 = 4
GCD (28 and 16) = 4
Example 2. Find the GCD of numbers 100 and 40
Decompose the number 100 into factors
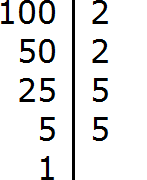
Decompose the number 40 into factors
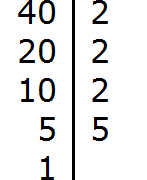
We got two decompositions: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5
Now from the expansion of the first number cross out the multipliers that are not included in the expansion of the second number. The expansion of the second number does not include one five (there is only one five). We will cross it out of the first expansion
Multiply the remaining numbers:
The answer is 20, so 20 is the greatest common divisor of 100 and 40. These two numbers are divided by 20 without a remainder:
100 : 20 = 5
40 : 20 = 2
GCD (100 and 40) = 20.
Example 3. Find the GCD of numbers 72 and 128
Decompose the number 72 into factors
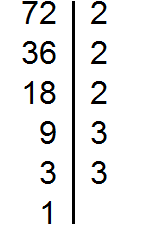
Decompose the number 128 into factors
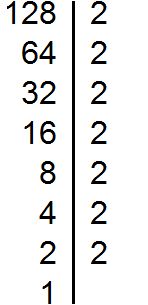2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.
Now from the expansion of the first number cross out the multipliers that are not included in the expansion of the second number. The expansion of the second number does not include two triples (they are not there at all). We cross them out of the first expansion:
Multiply the remaining numbers:
The answer is 8. So the number 8 is the greatest common divisor of 72 and 128. These two numbers are divided by 8 without a remainder:
72 : 8 = 9
128 : 8 = 16
GCD (72 and 128) = 8
Finding GCD for multiple numbers
The greatest common divisor can also be found for several numbers, not just for two. For this purpose, the numbers subject to the search for the greatest common divisor, decompose into prime factors, then find the product of the common prime factors of these numbers.
For example, find the GCD for numbers 18, 24, and 36
Decompose the number 18 into factors
Decompose the number 24 into factors
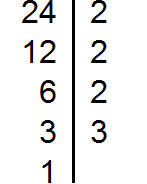
Decompose number 36 into factors
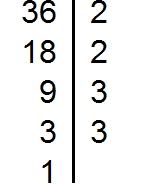
We got three decompositions:
Now find and underline the common multipliers:
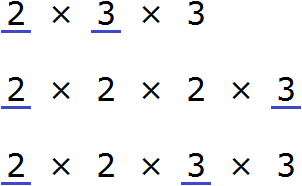
We see that the common multipliers for the numbers 18, 24, and 36 are multipliers 2 and 3. These multipliers are included in all three decompositions. By multiplying these multipliers, we get the GCD we are looking for:
2 × 3 = 6
The answer is 6. So 6 is the greatest common divisor of 18, 24, and 36. These three numbers are divided by 6 without a remainder:
18 : 6 = 3
24 : 6 = 4
36 : 6 = 6
GCD (18, 24 and 36) = 6
Example 2. Find GCD for numbers 12, 24, 36 and 42
Decompose each number into prime factors. Then find the product of common prime factors.
Decompose the number 12 into factors
Decompose the number 24 into factors
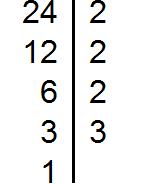
Decompose number 36 into factors
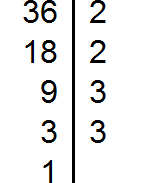
Decompose number 42 into factors
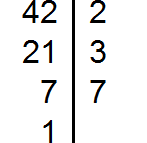
We got four decompositions:
Now find and underline the common multipliers:
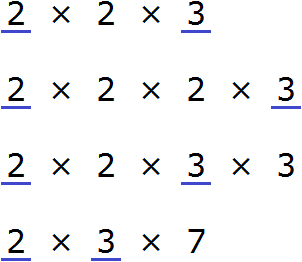
We see that the common multipliers for the numbers 12, 24, 36, and 42 are multipliers 2 and 3. By multiplying these multipliers, we get the GCD we are looking for:
2 × 3 = 6
The answer is 6. So 6 is the greatest common divisor of 12, 24, 36, and 42. These numbers are divided by 6 without a remainder:
12 : 6 = 2
24 : 6 = 4
36 : 6 = 6
42 : 6 = 7
GCD (12, 24 , 36 and 42) = 6
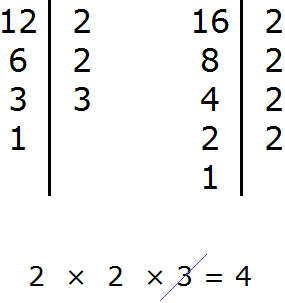
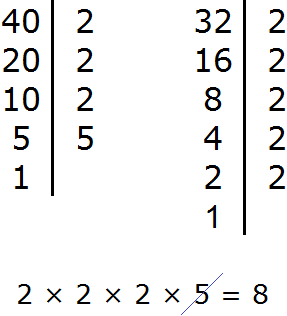
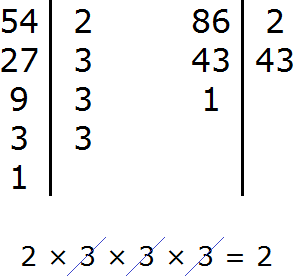
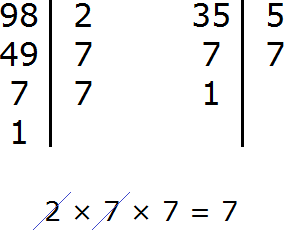
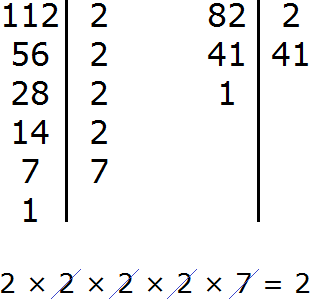
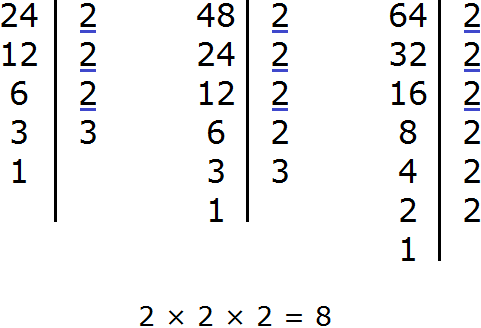
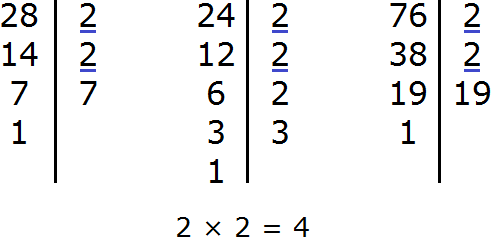
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.