Here are short articles answering one specific question.
When we write mixed numbers without a denominator, we convert them to decimals. When converting regular fractions into decimals, there are a few things we need to know, which we will talk about in a moment.
After the whole part is written, be sure to count the number of zeros in the denominator of the fractional part, because the number of zeros in the fractional part and the number of digits after the decimal point in the decimal must be the same. What does this mean? Consider the following example: Convert the mixed number ![]() into a decimal.
into a decimal.
First write down the whole part and put a dot:
3.
And you could immediately write down the numerator of the fractional part and the decimal is ready, but you have to count how many zeros are contained in the denominator of the fractional part.
So, let's calculate the number of zeroes in the fractional part of the mixed number ![]() . We see that the denominator of the fractional part is one zero. So the decimal will have one digit after the decimal point, and this digit will be the numerator of the fractional part of the mixed number
. We see that the denominator of the fractional part is one zero. So the decimal will have one digit after the decimal point, and this digit will be the numerator of the fractional part of the mixed number ![]() , that is, the number 2
, that is, the number 2
3.2
To convert a mixed repeating decimals to fractions, write in the numerator the difference where the minuend is the digits standing after the point in the fraction and the subtrahend are the digits standing between the point and the first period of the fractions.
For example, convert the mixed repeating decimal 0.31 (6) to fraction.
First, write the difference in the numerator. All digits after the decimal point (including the period) will be the decomposer, and the digits between the decimal point and the period will be the subtraction:
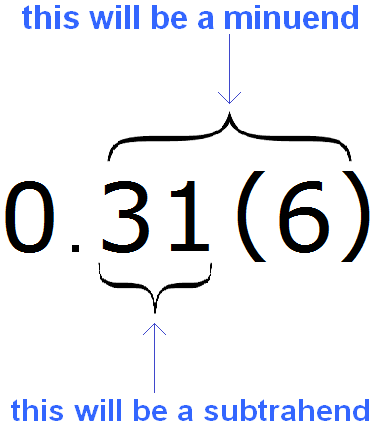
So we write the difference in the numerator:
Converting a purely repeating decimal to fractions is an operation that we will use rather rarely. Nevertheless, for general knowledge , it is important to study this as well. We will begin by converting a pure repeating decimal into an ordinary fraction.
We have already said that if a period in a repeating decimal begins immediately after the decimal point, such a fraction is called a purely periodic.
To convert a purely repeating decimal into an ordinary fraction, write the period of the repeating decimal in the numerator of the ordinary fraction, and write some number of nines in the denominator of the ordinary fraction. In this case, the number of nines must be equal to the number of digits in the period of the repeating decimal .
As an example, consider a purely repeating decimal 0. (3) - zero integers and three in the period. Let's try to convert it into a fraction.
The rule states that the period of a repeating decimal should be written first in the numerator of an ordinary fraction.
So in the numerator we write the period of the decimal 0. (3) that is three:
![]()
And the denominator must contain some number of nines. In this case, the number of nines must be equal to the number of digits in the period of the repeating decimal 0. (3).
Definition. The distributive law of multiplication says that any number which is multiplied by the sum of two or more numbers is equal to the sum of that number multiplied by each of the numbers separately.
Consider the following expression:
(3 + 5) × 2
We know that we must first perform the action in parentheses. We do it:
(3 + 5) = 8
In the main expression (3 + 5) × 2, replace the expression in parentheses with the resulting eight:
8 × 2 = 16
Here you will have to strain your brain and squeeze the most out of it, because dividing a multi-digit number by a multi-digit number is not that easy.
The principle of division is the same as before. Here you also need to find the first incomplete divisor. Here you can also find the remainder of the division.
First, we introduce a new concept - a round number. A round number is a number that ends in zero. For example, the following numbers are round:
10, 20, 30, 500, 600, 1000, 13000
Any number can be turned into a round number. To do this, the first digits forming the largest digit are left unchanged, and the remaining digits are replaced by zeros.
For example, let's turn number 19 into a round number. The first digit of the number 1 forms the most significant digit (digit of tens) - the digit is left as is, and the remaining 9 is replaced by zero. The result is 10.
Definition. The remainder is what is left of the action of division undivided.
For example, five divided by two would be two and one in the remainder:
5 : 2 = 2 (1 in the remainder)
You can check it by multiplication:
(2 x 2) + 1 = 5
Suppose we have five apples

Dividing a decimal by 0.1, 0.01, and 0.001 is done in the same way as dividing a decimal by a decimal. In the dividend and in the divisor you must move the point to the right by as many digits as there are after the point in the divisor.
For example, divide 6.3 by 0.1. First, move the dots in the dividend and divisor to the right by as many digits as there are after the dot in the divisor. There is one digit after the point in the dividend. So we move the points in the dividend and divisor to the right by one digit.
After moving the point to the right by one digit, the decimal 6.3 turns into the regular number 63, and the decimal 0.1 turns into a unit after moving the point to the right by one digit. And dividing 63 by 1 is very simple:
63 : 1 = 63
So the value of the expression 6.3 : 0.1 is 63
6.3 : 0.1 = 63
Dividing a decimal by 10, 100, or 1000 is done in the same way as dividing a decimal by a whole number. For example, divide 2.1 by 10. Solve this example with a column division:
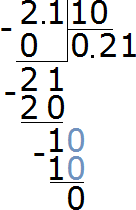
But there is a second way. It is easier. The essence of this method is that the point in the divisor is moved to the left by as many digits as there are zeros in the divisor.
Let's solve the previous example this way. 2,1 : 10. We look at the divisor. We are interested in how many zeroes are in it. We see that there is one zero. It means that in the divisor 2.1 we need to move the point to the left by one digit. We move the point to the left by one digit and see that there are no more digits left. In this case, we add another zero before the digit. As a result, we get 0.21
2.1 : 10 = 0.21
To divide a decimal by a decimal, you must move the dot to the right in the dividend and in the divisor to the same number of digits as there are after the dot in the dividend, and then divide by a regular number.
For example, divide 5.95 by 1.7
Write this expression in the corner
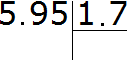
Now move the dot to the right in the divident and in the divisor to the same number of digits as there are after the point in the divisor. There is one digit after the dot in the divisor. So we must move the point to the right by one digit in the dividend and divisor. Let's move it:
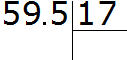
After moving the point to the right by one digit, the decimal 5.95 became 59.5. And the decimal 1.7, after moving the point to the right by one digit, turned into the regular number 17. And we already know how to divide a decimal by a regular number. Further calculation is not very difficult:
Let's say we have half a pizza:

Divide it equally between the two of us. How much pizza do we each get?
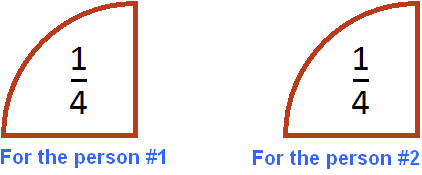
You can see that after splitting half of the pizza, there are two equal slices, each of which is ![]() of a pizza. So each person gets
of a pizza. So each person gets ![]() of a pizza.
of a pizza.
Division of fractions is done with inverse numbers. Inverse numbers allow you to replace division with multiplication.
To divide a fraction by a number, multiply the fraction by the number inverse of the divisor.
Using this rule, let's write down the division of our pizza half into two parts.
Situations often arise in life when you need to divide a smaller number by a larger one. For example, imagine a situation. There are three friends:

And you need to divide the two apples equally between them. How to do this? There are three friends and only two apples. We find ourselves in a situation where we need to divide a smaller number by a larger one (two apples for three).
The following rule is provided for such cases:
Dividing a smaller number by a larger number produces a fraction with the smaller-one divisor in the numerator and the bigger-one divisor in the denominator.
Page 3 of 9