Here you will have to strain your brain and squeeze the most out of it, because dividing a multi-digit number by a multi-digit number is not that easy.
The principle of division is the same as before. Here you also need to find the first incomplete divisor. Here you can also find the remainder of the division.
First, we introduce a new concept - a round number. A round number is a number that ends in zero. For example, the following numbers are round:
10, 20, 30, 500, 600, 1000, 13000
Any number can be turned into a round number. To do this, the first digits forming the largest digit are left unchanged, and the remaining digits are replaced by zeros.
For example, let's turn number 19 into a round number. The first digit of the number 1 forms the most significant digit (digit of tens) - the digit is left as is, and the remaining 9 is replaced by zero. The result is 10.
Another example. Let's turn number 125 into a round number. The first digit 1 forms the largest place (place of hundreds) - we leave the digit unchanged, and the remaining 25 digits are replaced with zeros. The result is 100.
Another example. Turn number 2431 into a round number. The first digit 2 is the largest digit (thousand digit), leave it unchanged, and replace the remaining digits 431 with zeros. The final result will be 2000.
Another example. Let's turn number 13735 into a round number. The first two digits of 13 form the large digit (tens of thousands) - leave these two digits unchanged, the remaining digits of 735 are replaced with zeros. The result is 13000.
Warning. In what follows, the concepts of round numbers and the translation of any number into a round number will be generalized.
Back to dividing multi-digit numbers by multi-digit numbers. The difficulty in dividing such numbers is that the fraction has to be found by matching. To do this, resort to various techniques, such as turning the divisor and the divisor into round numbers.
Example 1. Find the value of the expression 88 : 12
Write this expression with a corner:
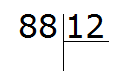
Ask the question how many numbers are 12 in the number 88? It's hard to answer from the first time. You have to reason.
We remember from school that the quotient was guessed by saying "take two" or "take three".
Let's try to guess the quotient. Unfortunately, you can't just take it from the sky. The quotient must be such that when it is multiplied by the divisor, the result is a number that is less than the divisor, but very close to it or equal to it.
Let's assume that the quotient is 2. Multiply this quotient by the divisor 12
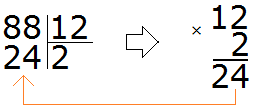
What does this give us? The resulting number is smaller than the divisor, but close to it? No. It is certainly less than the divisor 88, but very far from it. So two as a quotient doesn't fit. Let's guess the next number. Let's say the quotient is 5.
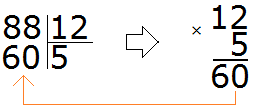
What does this give us? The resulting number is of course smaller, but it is not close to the divisible 88. So five as a quotient doesn't fit either. Let's try to take 8 at once.
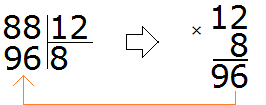
This time the resulting number is greater than the divisible number. And it should be less than the divisible, but very close to it or equal to it. So eight as a quotient doesn't fit either.
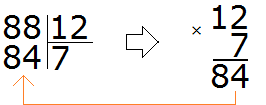
We finally found the right quotient! By multiplying the quotient 7 by the divisor 12, we get 84, which is less than the divisor, but close to it. Now we find the remainder of the division. To do this, we subtract 84 from 88 and get 4.
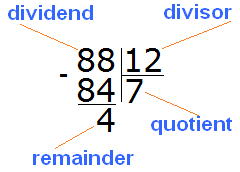
88 : 12 = 7 (4 left over)
Check: (12 x 7) + 4 = 84 + 4 = 88
As you can see from the example, it takes precious time to pick up a private. If we are sitting for a test or an exam, where every minute is important, this method will obviously not help us.
To save time, you can turn the divisor and the divisor into round numbers and then divide those round numbers. Dividing round numbers is much easier and more convenient.
For example, to divide 90 by 10, just take away the zeros from both numbers and divide 9 by 1. The result will be 90 : 10 = 9.
The number of zeroes to be discarded must be strictly the same. For example, if we divide 900 by 90, then we drop a zero from each number, because 900 has two zeros, and 90 has only one. By dropping a zero from each number, we get the expression 90 : 9 = 10. We end up with 900 : 90 = 10.
There is also nothing complicated about dividing round numbers. Try to understand it. If you don't understand it, study it several times. This is very important.
Here are some examples of how to divide round numbers. The zeros to be discarded are shaded in gray:
800 : 10 = 80 (discard each zero and divide 80 by 1, you get 80)
800 : 80 = 10 (truncated by zero and divided 80 by 8, so we have 10)
900 : 10 = 90 (truncated by zero and divided by 90 divided by 1, so you get 90)
400 : 50 = 8 (truncated by zero and divided 40 by 5, yielding 8)
320 : 80 = 4 (zero was truncated and 32 divided by 8, yielding 4)
If you've noticed, it all comes down to the multiplication table in the end. That's why schools require you to know it by heart. We require it too, although we don't force it.
Now let's solve the previous example 88 : 12 where we were struggling to find the quotient by guessing. First, turn the divisor and the divisor into round numbers.
The round number for 88 is 80.
And the round number for 12 is 10.
Now divide the resulting round numbers:
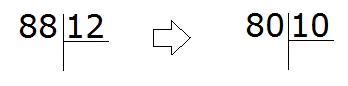
Now we check if the quotient is correct. To do this, we multiply the quotient by the divisor (8 by 12). We already checked the eight as a quotient when we solved this example by guessing. It did not fit, because after multiplying it by the divisor, we got the number 96, which is larger than the divisor. But the quotient 7, which is less than eight by only one, did fit.
From this, we can conclude that in the expression 88 : 12, the quotient obtained by turning the divisor and the divisor into round numbers is greater by only one. Our task is to reduce this quotient by one.
So let's reduce 8 by one: 8 - 1 = 7. Seven is the quotient. Write it in the right corner of our example:

As you can see, we solved this example much faster this way.
Example 2. Find the value of the expression 1296 : 144
Write this expression in the corner. Immediately we find the first incomplete divisor. It is formed by all four digits of the divisor:
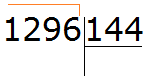
This is dividing a multi-digit number by a multi-digit number. Let's apply the method we just learned. Let's turn the divisor and the divisor into round numbers and then divide them.
For the divisor 1296, the round number is 1000. And for the divisor 144, the round number is 100.
Divide 1000 by 100, and we get 10. Check the resulting 10 by multiplying it by the divisor 144
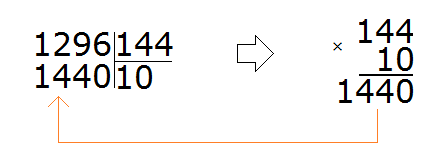
The tens don't fit, because multiplication produces a number that is greater than the divisor.
Let's try to take 9 by decreasing the tens by one.
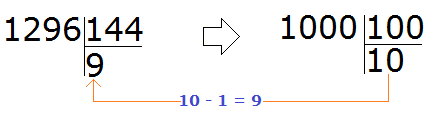
We check the nine. To do this we multiply it by the divisor:
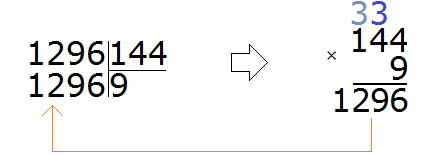
Beautiful! The resulting number was not only closer to the divisible, but also equal to it. This means that the division was done without a remainder. Complete this example by subtracting the resulting number 1296 from 1296
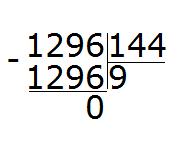
1296 : 144 = 9
Check: 144 x 9 = 1296
Example 3. Let's try to solve a big and complicated example 227,492 : 331
Write this expression in the corner. Immediately determine the first incomplete divisor. It is formed by the first four digits of the divisible 2274. So we first divide 2274 by 331. Let's turn them into round numbers.
For 2274, the round number is 2000. And for 331 the round number is 300.
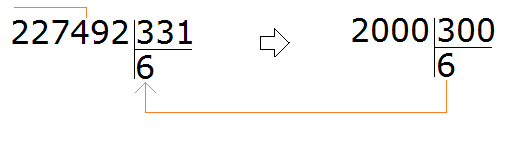
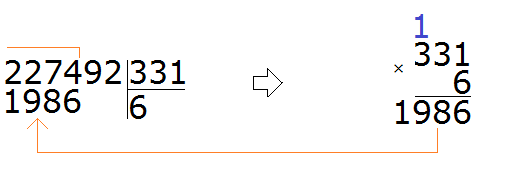
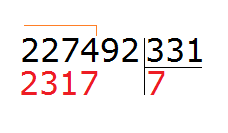
If we were to take a 7 and check that 7, we would get 2317, which is greater than the divisor, and that is not allowed.
We continue to solve our example. Subtract 1986 from 2274, we get 288:
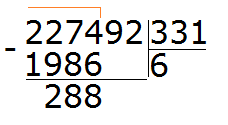
288 is the remainder of dividing 2274 by 331. Next, to continue dividing, you need to take down a nine:
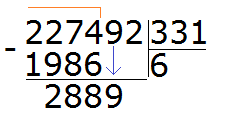
Now we have to divide 2889 by 331. Turn them into round numbers and divide them. Immediately check the quotient obtained in this way:
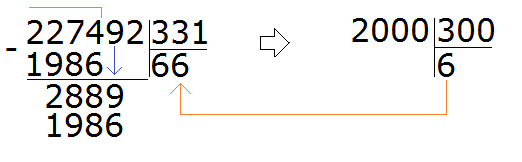
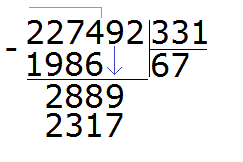
We checked the seven. Again we got a number that is far from the divisor 2889. So the seven does not fit either. Let's check the eight:

The eight fits. It answers the question of how many numbers 331 are in 2889. If we took nine each, then multiplying by the divisor, we would get the number 2979, which is already more than the divisor 2889.
Now we take out the remainder of the division of 2889 by 331. To do this, we subtract 2648 from 2889 and get 241.
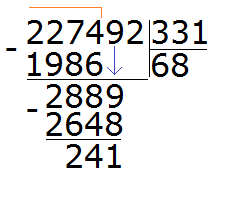
241 is the remainder of dividing 2889 by 331. To continue dividing, remove 2 from the main divisor:
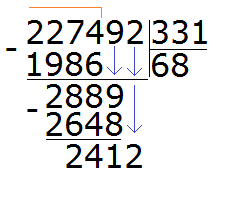
Now divide 2412 by 331. Let's take 7
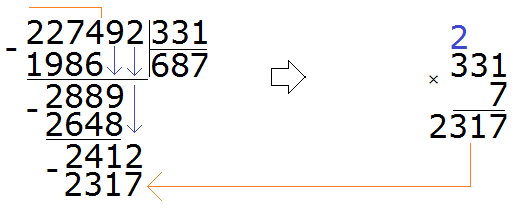
Now we find the last residue. To do this, we subtract 2317 from 2412 and get 95. This completes the example:

227492 : 331 = 687 (95 in balance)
Check: (331 x 687) + 95= 227 397 + 95 = 227 492
This is the end of this lesson. Don't be upset if you don't immediately learn how to divide numbers by a corner. This skill is built up over time, combined with intensive training. Mistakes are not terrible. The most important thing is to understand.
Note that in this lesson we will only look at division with a remainder. We will consider division without the remainder in the next lessons. This is done in order not to make learning difficult. As they say, all in good time.
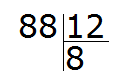

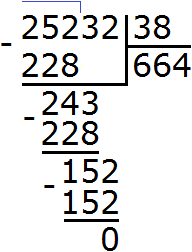
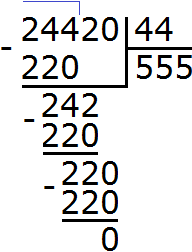
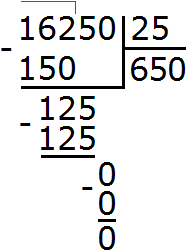
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.