Here are short articles answering one specific question.
Long subtraction
Example 1. Subtract number 53 from number 69.
Write down the numbers in columns. Units under ones, tens under tens. Then subtract by digits. Subtract the units of the first number from the units of the second number. Subtract the tens of the first number from the tens of the second number:
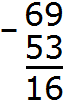
We got the answer 16.
Now we are going to learn about a very interesting topic in math. It is called "inverse numbers".
Definition. The inverse of a is a number which, when multiplied by a, yields one.
Let's substitute the number 5 in place of the variable a in this definition and try to read the definition:
The inverse of 5 is a number that, when multiplied by 5, gives one.
Is it possible to find a number that, when multiplied by 5, gives one? It is possible. Let's represent five as a fraction:
![]()
Then multiply this fraction by itself, but swap the numerator and denominator. In other words, multiply fraction ![]() by itself, only inverted:
by itself, only inverted:
From the previous lesson we know that if any number is divisible by another number without a remainder, it is called a multiple of that number.
It turns out that a multiple can be common to several numbers. And now we will be interested in the multiple of two numbers, and it should be as small as possible.
Definition. The least common multiple (LCM) of a and b is the smallest number that is a multiple of a and b. In other words, it is the smallest number that is divisible without a remainder by a and b.
The definition contains two variables a and b. Let's substitute any two numbers for these variables. For example, instead of variable a, let's substitute number 9, and instead of variable b, let's substitute number 12. Now let's try to read the definition:
The least common multiple (LCM) of 9 and 12 is the smallest number that is a multiple of 9 and 12. In other words, it is the smallest number that is divisible without a remainder by 9 and by 12..
When you need to divide a large number, it is a must to use this method.
Before long division, you must know:
- normal division of small numbers;
- division with a remainder;
- long multiplication;
- long subtraction.
Let's look at the long division with a simple example. Let us find the value of the expression 9 : 3. The long division is written as follows:
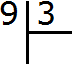
To multiply any number by 10, 100 or 1000, just add to the first multiplier the number of zeros from the 10/100/1000.
For example, to multiply 12 by 10, you need to add zero from the multiplier 10 to the multiplier 12. The answer is 120

To multiply fractions, multiply their numerators and denominators. If the answer is an improper fraction, select the whole part of the fraction.
Example 1. Find the value of the expression ![]() .
.
Multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
![]()
The answer is ![]() . It is desirable to reduce this fraction. Fraction
. It is desirable to reduce this fraction. Fraction ![]() can be reduced by 2. Then the final solution will look like this:
can be reduced by 2. Then the final solution will look like this:
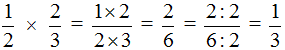
To multiply a fraction by a number, multiply the numerator of the fraction by that number and leave the denominator unchanged.
Example 1. Multiply a fraction ![]() by the number 1.
by the number 1.
Multiply the numerator of the fraction ![]() by the number 1.
by the number 1.
![]()
The entry![]() can be understood as taking half 1 time. For example, if you take
can be understood as taking half 1 time. For example, if you take ![]() a pizza once, you get
a pizza once, you get ![]() pizzas
pizzas
Multiplying multi-digit numbers by multi-digit numbers is done in the same way as multiplying multi-digit numbers by single-digit numbers. Each digit of a multi-digit number is multiplied by each digit of another multi-digit number. The only difference is that at the end there is a kind of staircase of answers that must be added up. Let's look at a few examples to get a good understanding of this.
Example 1. Find the value of the expression 12 x 14
Write down this expression in a column - ones under ones, tens under tens:
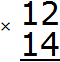
One-digit numbers are easy to multiply. All you need to know is the multiplication table. Examples:
5 x 5 = 25
3 x 5 = 15
7 x 6 = 42
5 x 8 = 40
Sometimes situations arise where you want to multiply a decimal by a whole number.
To multiply a decimal and a whole number, you must multiply them without paying attention to the dot in the decimal. Once you have the answer, you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in the decimal, then count as many digits to the right in the answer and put a dot.
For example, multiply 2.54 by 2
Multiply the decimal 2.54 by the whole number 2, ignoring the dot:
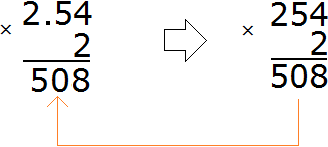
We got the number 508. In this number you need to separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in the fraction 2.54. There are two digits after the dot in the fraction 2.54.
Multiplying decimals is easy and even fun. To multiply decimals, you have to multiply them like regular numbers without paying attention to the dots.
When you get the answer, you must separate the whole part from the fractional part with a dot. To do this, count the number of digits after the dot in both fractions, then count as many digits to the right in the answer and put a dot.
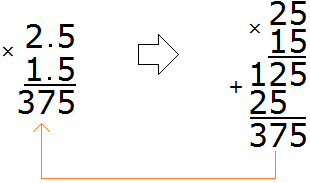
Example 1. Find the value of the expression 2.5 × 1.5
Multiply these decimals as regular numbers, ignoring the dots. To ignore the dots, you can pretend for a while that they do not exist at all:
Page 6 of 9